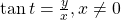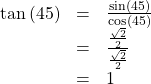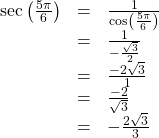Chapter 3.5: The Other Trigonometric Functions
Learning Objectives
In this section you will:
- Find exact values of the trigonometric functions secant, cosecant, tangent, and cotangent of
 and
and 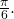
- Use reference angles to evaluate the trigonometric functions secant, tangent, and cotangent.
- Use properties of even and odd trigonometric functions.
- Recognize and use fundamental identities.
- Evaluate trigonometric functions with a calculator.
A wheelchair ramp that meets the standards of the Americans with Disabilities Act must make an angle with the ground whose tangent is ![]() or less, regardless of its length. A tangent represents a ratio, so this means that for every 1 inch of rise, the ramp must have 12 inches of run. Trigonometric functions allow us to specify the shapes and proportions of objects independent of exact dimensions. We have already defined the sine and cosine functions of an angle. Though sine and cosine are the trigonometric functions most often used, there are four others. Together they make up the set of six trigonometric functions. In this section, we will investigate the remaining functions.
or less, regardless of its length. A tangent represents a ratio, so this means that for every 1 inch of rise, the ramp must have 12 inches of run. Trigonometric functions allow us to specify the shapes and proportions of objects independent of exact dimensions. We have already defined the sine and cosine functions of an angle. Though sine and cosine are the trigonometric functions most often used, there are four others. Together they make up the set of six trigonometric functions. In this section, we will investigate the remaining functions.
Finding Exact Values of the Trigonometric Functions Secant, Cosecant, Tangent, and Cotangent
We can also define the remaining functions in terms of the unit circle with a point ![]() corresponding to an angle of
corresponding to an angle of ![]() as shown in (Figure). As with the sine and cosine, we can use the
as shown in (Figure). As with the sine and cosine, we can use the ![]() coordinates to find the other functions.
coordinates to find the other functions.

The first function we will define is the tangent. The tangent of an angle is the ratio of the y-value to the x-value of the corresponding point on the unit circle. In (Figure), the tangent of angle ![]() is equal to
is equal to ![]() Because the y-value is equal to the sine of
Because the y-value is equal to the sine of ![]() and the x-value is equal to the cosine of
and the x-value is equal to the cosine of ![]() the tangent of angle
the tangent of angle ![]() can also be defined as
can also be defined as ![]() The tangent function is abbreviated as
The tangent function is abbreviated as ![]() The remaining three functions can all be expressed as reciprocals of functions we have already defined.
The remaining three functions can all be expressed as reciprocals of functions we have already defined.
- The secant function is the reciprocal of the cosine function. In (Figure), the secant of angle
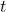 is equal to
is equal to 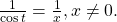 The secant function is abbreviated as
The secant function is abbreviated as 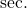
- The cotangent function is the reciprocal of the tangent function. In (Figure), the cotangent of angle
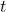 is equal to
is equal to 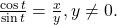 The cotangent function is abbreviated as
The cotangent function is abbreviated as 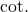
- The cosecant function is the reciprocal of the sine function. In (Figure), the cosecant of angle
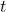 is equal to
is equal to 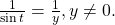 The cosecant function is abbreviated as
The cosecant function is abbreviated as 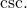
Tangent, Secant, Cosecant, and Cotangent Functions
If ![]() is a real number and
is a real number and ![]() is a point where the terminal side of an angle of
is a point where the terminal side of an angle of ![]() radians intercepts the unit circle, then
radians intercepts the unit circle, then
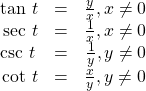
Finding Trigonometric Functions from a Point on the Unit Circle
The point ![]() is on the unit circle, as shown in (Figure). Find
is on the unit circle, as shown in (Figure). Find ![]() and
and ![]()

Show Solution
Because we know the ![]() coordinates of the point on the unit circle indicated by angle
coordinates of the point on the unit circle indicated by angle ![]() we can use those coordinates to find the six functions:
we can use those coordinates to find the six functions:
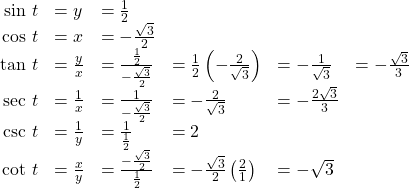
Try It
The point ![]() is on the unit circle, as shown in (Figure). Find
is on the unit circle, as shown in (Figure). Find ![]() and
and ![]()

Show Solution
![]()
Finding the Trigonometric Functions of an Angle
Find ![]() and
and ![]() when
when ![]()
Show Solution
We have previously used the properties of equilateral triangles to demonstrate that ![]() and
and ![]() We can use these values and the definitions of tangent, secant, cosecant, and cotangent as functions of sine and cosine to find the remaining function values.
We can use these values and the definitions of tangent, secant, cosecant, and cotangent as functions of sine and cosine to find the remaining function values.
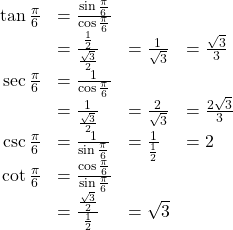
Try It
Find ![]() and
and ![]() when
when ![]()
Show Solution
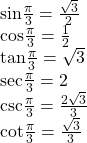
Because we know the sine and cosine values for the common first-quadrant angles, we can find the other function values for those angles as well by setting ![]() equal to the cosine and
equal to the cosine and ![]() equal to the sine and then using the definitions of tangent, secant, cosecant, and cotangent. The results are shown in (Figure).
equal to the sine and then using the definitions of tangent, secant, cosecant, and cotangent. The results are shown in (Figure).
| Angle | |||||
|---|---|---|---|---|---|
| Cosine | 1 | 0 | |||
| Sine | 0 | 1 | |||
| Tangent | 0 | 1 | Undefined | ||
| Secant | 1 | 2 | Undefined | ||
| Cosecant | Undefined | 2 | 1 | ||
| Cotangent | Undefined | 1 | 0 |
Using Reference Angles to Evaluate Tangent, Secant, Cosecant, and Cotangent
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles as we have already done with the sine and cosine functions. The procedure is the same: Find the reference angle formed by the terminal side of the given angle with the horizontal axis. The trigonometric function values for the original angle will be the same as those for the reference angle, except for the positive or negative sign, which is determined by x– and y-values in the original quadrant. (Figure) shows which functions are positive in which quadrant.
To help remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “A Smart Trig Class.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the six trigonometric functions are positive. In quadrant II, “Smart,” only sine and its reciprocal function, cosecant, are positive. In quadrant III, “Trig,” only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Class,” only cosine and its reciprocal function, secant, are positive.

How To
Given an angle not in the first quadrant, use reference angles to find all six trigonometric functions.
- Measure the angle formed by the terminal side of the given angle and the horizontal axis. This is the reference angle.
- Evaluate the function at the reference angle.
- Observe the quadrant where the terminal side of the original angle is located. Based on the quadrant, determine whether the output is positive or negative.
Using Reference Angles to Find Trigonometric Functions
Use reference angles to find all six trigonometric functions of ![]()
Show Solution
The angle between this angle’s terminal side and the x-axis is ![]() so that is the reference angle. Since
so that is the reference angle. Since ![]() is in the third quadrant, where both
is in the third quadrant, where both ![]() and
and ![]() are negative, cosine, sine, secant, and cosecant will be negative, while tangent and cotangent will be positive.
are negative, cosine, sine, secant, and cosecant will be negative, while tangent and cotangent will be positive.
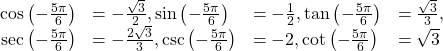
Try It
Use reference angles to find all six trigonometric functions of ![]()
Show Solution
![]()
Using Even and Odd Trigonometric Functions
To be able to use our six trigonometric functions freely with both positive and negative angle inputs, we should examine how each function treats a negative input. As it turns out, there is an important difference among the functions in this regard.
Consider the function ![]() shown in (Figure). The graph of the function is symmetrical about the y-axis. All along the curve, any two points with opposite x-values have the same function value. This matches the result of calculation:
shown in (Figure). The graph of the function is symmetrical about the y-axis. All along the curve, any two points with opposite x-values have the same function value. This matches the result of calculation: ![]() and so on. So
and so on. So ![]() is an even function, a function such that two inputs that are opposites have the same output. That means
is an even function, a function such that two inputs that are opposites have the same output. That means ![]()

 is an even function.
is an even function.Now consider the function ![]() shown in (Figure). The graph is not symmetrical about the y-axis. All along the graph, any two points with opposite x-values also have opposite y-values. So
shown in (Figure). The graph is not symmetrical about the y-axis. All along the graph, any two points with opposite x-values also have opposite y-values. So ![]() is an odd function, one such that two inputs that are opposites have outputs that are also opposites. That means
is an odd function, one such that two inputs that are opposites have outputs that are also opposites. That means ![]()

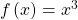 is an odd function.
is an odd function.We can test whether a trigonometric function is even or odd by drawing a unit circle with a positive and a negative angle, as in (Figure). The sine of the positive angle is ![]() The sine of the negative angle is
The sine of the negative angle is ![]() The sine function, then, is an odd function. We can test each of the six trigonometric functions in this fashion. The results are shown in (Figure).
The sine function, then, is an odd function. We can test each of the six trigonometric functions in this fashion. The results are shown in (Figure).

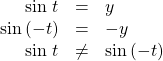 |
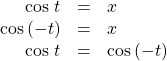 |
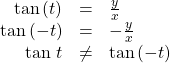 |
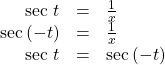 |
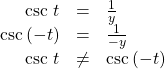 |
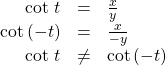 |
Even and Odd Trigonometric Functions
An even function is one in which ![]()
An odd function is one in which ![]()
Cosine and secant are even:
Sine, tangent, cosecant, and cotangent are odd:
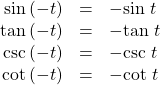
Using Even and Odd Properties of Trigonometric Functions
If the secant of angle ![]() is 2, what is the secant of
is 2, what is the secant of ![]()
Show Solution
Secant is an even function. The secant of an angle is the same as the secant of its opposite. So if the secant of angle ![]() is 2, the secant of
is 2, the secant of ![]() is also 2.
is also 2.
Try It
If the cotangent of angle ![]() is
is ![]() what is the cotangent of
what is the cotangent of ![]()
Show Solution
![]()
Recognizing and Using Fundamental Identities
We have explored a number of properties of trigonometric functions. Now, we can take the relationships a step further, and derive some fundamental identities. Identities are statements that are true for all values of the input on which they are defined. Usually, identities can be derived from definitions and relationships we already know. For example, the Pythagorean Identity we learned earlier was derived from the Pythagorean Theorem and the definitions of sine and cosine.
Fundamental Identities
We can derive some useful identities from the six trigonometric functions. The other four trigonometric functions can be related back to the sine and cosine functions using these basic relationships:
Using Identities to Evaluate Trigonometric Functions
- Given
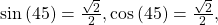 evaluate
evaluate 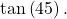
- Given
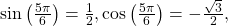 evaluate
evaluate 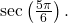
Show Solution
Because we know the sine and cosine values for these angles, we can use identities to evaluate the other functions.
Try It
Evaluate ![]()
Show Solution
![]()
Using Identities to Simplify Trigonometric Expressions
Simplify ![]()
Show Solution
We can simplify this by rewriting both functions in terms of sine and cosine.

By showing that ![]() can be simplified to
can be simplified to ![]() we have, in fact, established a new identity.
we have, in fact, established a new identity.
Try It
Simplify ![]()
Show Solution
![]()
Alternate Forms of the Pythagorean Identity
We can use these fundamental identities to derive alternate forms of the Pythagorean Identity, ![]() One form is obtained by dividing both sides by
One form is obtained by dividing both sides by ![]()
The other form is obtained by dividing both sides by ![]()
Alternate Forms of the Pythagorean Identity
Using Identities to Relate Trigonometric Functions
If ![]() and
and ![]() is in quadrant IV, as shown in (Figure), find the values of the other five trigonometric functions.
is in quadrant IV, as shown in (Figure), find the values of the other five trigonometric functions.

Show Solution
![]() and the remaining functions by relating them to sine and cosine.
and the remaining functions by relating them to sine and cosine.
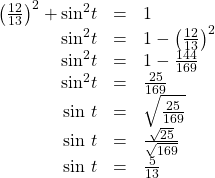
The sign of the sine depends on the y-values in the quadrant where the angle is located. Since the angle is in quadrant IV, where the y-values are negative, its sine is negative, ![]()
The remaining functions can be calculated using identities relating them to sine and cosine.
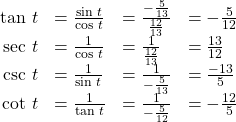
Try It
If ![]() and
and ![]() find the values of the other five functions.
find the values of the other five functions.
Show Solution
![]()
As we discussed at the beginning of the chapter, a function that repeats its values in regular intervals is known as a periodic function. The trigonometric functions are periodic. For the four trigonometric functions, sine, cosine, cosecant and secant, a revolution of one circle, or ![]() will result in the same outputs for these functions. And for tangent and cotangent, only a half a revolution will result in the same outputs.
will result in the same outputs for these functions. And for tangent and cotangent, only a half a revolution will result in the same outputs.
Other functions can also be periodic. For example, the lengths of months repeat every four years. If ![]() represents the length time, measured in years, and
represents the length time, measured in years, and ![]() represents the number of days in February, then
represents the number of days in February, then ![]() This pattern repeats over and over through time. In other words, every four years, February is guaranteed to have the same number of days as it did 4 years earlier. The positive number 4 is the smallest positive number that satisfies this condition and is called the period. A period is the shortest interval over which a function completes one full cycle—in this example, the period is 4 and represents the time it takes for us to be certain February has the same number of days.
This pattern repeats over and over through time. In other words, every four years, February is guaranteed to have the same number of days as it did 4 years earlier. The positive number 4 is the smallest positive number that satisfies this condition and is called the period. A period is the shortest interval over which a function completes one full cycle—in this example, the period is 4 and represents the time it takes for us to be certain February has the same number of days.
Period of a Function
The period ![]() of a repeating function
of a repeating function ![]() is the number representing the interval such that
is the number representing the interval such that ![]() for any value of
for any value of ![]()
The period of the cosine, sine, secant, and cosecant functions is ![]()
The period of the tangent and cotangent functions is ![]()
Finding the Values of Trigonometric Functions
Find the values of the six trigonometric functions of angle ![]() based on (Figure).
based on (Figure).

Show Solution
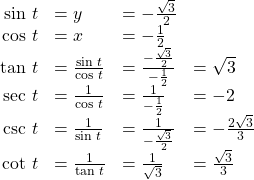
Try It
Find the values of the six trigonometric functions of angle ![]() based on (Figure).
based on (Figure).

Show Solution
![]()
Finding the Value of Trigonometric Functions
If ![]()
Show Solution
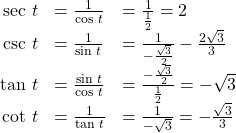
Try It
![]()
Show Solution
![]()
Evaluating Trigonometric Functions with a Calculator
We have learned how to evaluate the six trigonometric functions for the common first-quadrant angles and to use them as reference angles for angles in other quadrants. To evaluate trigonometric functions of other angles, we use a scientific or graphing calculator or computer software. If the calculator has a degree mode and a radian mode, confirm the correct mode is chosen before making a calculation.
Evaluating a tangent function with a scientific calculator as opposed to a graphing calculator or computer algebra system is like evaluating a sine or cosine: Enter the value and press the TAN key. For the reciprocal functions, there may not be any dedicated keys that say CSC, SEC, or COT. In that case, the function must be evaluated as the reciprocal of a sine, cosine, or tangent.
If we need to work with degrees and our calculator or software does not have a degree mode, we can enter the degrees multiplied by the conversion factor ![]() to convert the degrees to radians. To find the secant of
to convert the degrees to radians. To find the secant of ![]() we could press
we could press
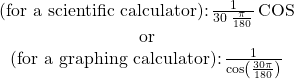
How To
Given an angle measure in radians, use a scientific calculator to find the cosecant.
- If the calculator has degree mode and radian mode, set it to radian mode.
- Enter:
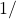
- Enter the value of the angle inside parentheses.
- Press the SIN key.
- Press the = key.
How To
Given an angle measure in radians, use a graphing utility/calculator to find the cosecant.
- If the graphing utility has degree mode and radian mode, set it to radian mode.
- Enter:
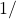
- Press the SIN key.
- Enter the value of the angle inside parentheses.
- Press the ENTER key.
Evaluating the Cosecant Using Technology
Evaluate the cosecant of ![]()
Show Solution
For a scientific calculator, enter information as follows:
Try It
Evaluate the cotangent of ![]()
Show Solution
![]()
Access these online resources for additional instruction and practice with other trigonometric functions.
Key Equations
| Tangent function | |
| Secant function | |
| Cosecant function | |
| Cotangent function |
Key Concepts
- The tangent of an angle is the ratio of the y-value to the x-value of the corresponding point on the unit circle.
- The secant, cotangent, and cosecant are all reciprocals of other functions. The secant is the reciprocal of the cosine function, the cotangent is the reciprocal of the tangent function, and the cosecant is the reciprocal of the sine function.
- The six trigonometric functions can be found from a point on the unit circle. See (Figure).
- Trigonometric functions can also be found from an angle. See (Figure).
- Trigonometric functions of angles outside the first quadrant can be determined using reference angles. See (Figure).
- A function is said to be even if
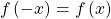 and odd if
and odd if 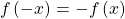 for all x in the domain of f.
for all x in the domain of f. - Cosine and secant are even; sine, tangent, cosecant, and cotangent are odd.
- Even and odd properties can be used to evaluate trigonometric functions. See (Figure).
- The Pythagorean Identity makes it possible to find a cosine from a sine or a sine from a cosine.
- Identities can be used to evaluate trigonometric functions. See (Figure) and (Figure).
- Fundamental identities such as the Pythagorean Identity can be manipulated algebraically to produce new identities. See (Figure).
- The trigonometric functions repeat at regular intervals.
- The period
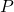 of a repeating function
of a repeating function 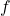 is the smallest interval such that
is the smallest interval such that 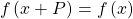 for any value of
for any value of 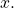
- The values of trigonometric functions can be found by mathematical analysis. See (Figure) and (Figure).
- To evaluate trigonometric functions of other angles, we can use a calculator or computer software. See (Figure).
Section Exercises
Verbal
1. On an interval of ![]() can the sine and cosine values of a radian measure ever be equal? If so, where?
can the sine and cosine values of a radian measure ever be equal? If so, where?
Show Solution
Yes, when the reference angle is ![]() and the terminal side of the angle is in quadrants I and III. Thus, a
and the terminal side of the angle is in quadrants I and III. Thus, a ![]() the sine and cosine values are equal.
the sine and cosine values are equal.
2. What would you estimate the cosine of ![]() degrees to be? Explain your reasoning.
degrees to be? Explain your reasoning.
3. For any angle in quadrant II, if you knew the sine of the angle, how could you determine the cosine of the angle?
Show Solution
Substitute the sine of the angle in for ![]() in the Pythagorean Theorem
in the Pythagorean Theorem ![]() Solve for
Solve for ![]() and take the negative solution.
and take the negative solution.
4. Describe the secant function.
5. Tangent and cotangent have a period of ![]() What does this tell us about the output of these functions?
What does this tell us about the output of these functions?
Show Solution
The outputs of tangent and cotangent will repeat every ![]() units.
units.
Algebraic
For the following exercises, find the exact value of each expression.
6. ![]()
7. ![]()
Show Solution
![]()
8. ![]()
9. ![]()
Show Solution
![]()
10. ![]()
11. ![]()
Show Solution
![]()
12. ![]()
13. ![]()
Show Solution
1
14. ![]()
15. ![]()
Show Solution
2
16. ![]()
17. ![]()
Show Solution
![]()
For the following exercises, use reference angles to evaluate the expression.
18. ![]()
19. ![]()
Show Solution
![]()
20. ![]()
21. ![]()
Show Solution
![]()
22. ![]()
23. ![]()
Show Solution
![]()
24. ![]()
25. ![]()
Show Solution
–1
26. ![]()
27. ![]()
Show Solution
-2
29. ![]()
Show Solution
![]()
30. ![]()
31. ![]()
Show Solution
2
32. ![]()
33. ![]()
Show Solution
![]()
34. ![]()
35. ![]()
Show Solution
–2
36. ![]()
37. ![]()
Show Solution
–1
38. If ![]() and
and ![]() is in quadrant II, find
is in quadrant II, find ![]() and
and ![]()
39. If ![]() and
and ![]() is in quadrant III, find
is in quadrant III, find ![]() and
and ![]()
Show Solution
![]()
40. If ![]() and
and ![]() find
find ![]()
41. If ![]() and
and ![]() find
find ![]() and
and ![]()
Show Solution
![]()
![]()
![]()
![]()
42. If ![]() and
and ![]() find
find ![]() and
and ![]()
43. If ![]() what is the
what is the ![]()
Show Solution
![]()
44. If ![]() what is the
what is the ![]()
45. If ![]() what is the
what is the ![]()
Show Solution
3.1
46. If ![]() what is the
what is the ![]()
47. If ![]() what is the
what is the ![]()
Show Solution
1.4
48. If ![]() what is the
what is the ![]()
Graphical
For the following exercises, use the angle in the unit circle to find the value of the each of the six trigonometric functions.

Show Solution
![]()


Show Solution
![]()
Technology
For the following exercises, use a graphing calculator to evaluate to three decimal places.
52. ![]()
53. ![]()
Show Solution
–0.228
54. ![]()
55. ![]()
Show Solution
–2.414
56. ![]()
57. ![]()
Show Solution
1.414
58. ![]()
59. ![]()
Show Solution
1.540
60. ![]()
61. ![]()
Show Solution
1.556
Extensions
For the following exercises, use identities to evaluate the expression.
62. If ![]() and
and ![]() find
find ![]()
63. If ![]() and
and ![]() find
find ![]()
Show Solution
![]()
64. If ![]() and
and ![]() find
find ![]()
65. If ![]() and
and ![]() find
find ![]()
Show Solution
![]()
67. Determine whether the function ![]() is even, odd, or neither.
is even, odd, or neither.
68. Determine whether the function ![]() is even, odd, or neither.
is even, odd, or neither.
Show Solution
even
69. Determine whether the function ![]() is even, odd, or neither.
is even, odd, or neither.
70. Determine whether the function ![]() is even, odd, or neither.
is even, odd, or neither.
Show Solution
even
For the following exercises, use identities to simplify the expression.
71. ![]()
72. ![]()
Show Solution
![]()
Real-World Applications
73. The amount of sunlight in a certain city can be modeled by the function ![]() where
where ![]() represents the hours of sunlight, and
represents the hours of sunlight, and ![]() is the day of the year. Use the equation to find how many hours of sunlight there are on February 10, the 42nd day of the year. State the period of the function.
is the day of the year. Use the equation to find how many hours of sunlight there are on February 10, the 42nd day of the year. State the period of the function.
74. The amount of sunlight in a certain city can be modeled by the function ![]() where
where ![]() represents the hours of sunlight, and
represents the hours of sunlight, and ![]() is the day of the year. Use the equation to find how many hours of sunlight there are on September 24, the 267th day of the year. State the period of the function.
is the day of the year. Use the equation to find how many hours of sunlight there are on September 24, the 267th day of the year. State the period of the function.
Show Solution
13.77 hours, period: ![]()
75. The equation ![]() models the blood pressure,
models the blood pressure, ![]() where
where ![]() represents time in seconds. (a) Find the blood pressure after 15 seconds. (b) What are the maximum and minimum blood pressures?
represents time in seconds. (a) Find the blood pressure after 15 seconds. (b) What are the maximum and minimum blood pressures?
76. The height of a piston, ![]() in inches, can be modeled by the equation
in inches, can be modeled by the equation ![]() where
where ![]() represents the crank angle. Find the height of the piston when the crank angle is
represents the crank angle. Find the height of the piston when the crank angle is ![]()
Show Solution
7.73 inches
77. The height of a piston, ![]() in inches, can be modeled by the equation
in inches, can be modeled by the equation ![]() where
where ![]() represents the crank angle. Find the height of the piston when the crank angle is
represents the crank angle. Find the height of the piston when the crank angle is ![]()
Chapter Review Exercises
Angles
For the following exercises, convert the angle measures to degrees.
1. ![]()
Show Solution
![]()
2. ![]()
For the following exercises, convert the angle measures to radians.
3. ![]()
Show Solution
![]()
4. ![]()
5. Find the length of an arc in a circle of radius 7 meters subtended by the central angle of ![]()
Show Solution
10.385 meters
6. Find the area of the sector of a circle with diameter 32 feet and an angle of ![]() radians.
radians.
For the following exercises, find the angle between ![]() and
and ![]() that is coterminal with the given angle.
that is coterminal with the given angle.
7. ![]()
Show Solution
![]()
8. ![]()
For the following exercises, find the angle between 0 and ![]() in radians that is coterminal with the given angle.
in radians that is coterminal with the given angle.
9. ![]()
Show Solution
![]()
10. ![]()
For the following exercises, draw the angle provided in standard position on the Cartesian plane.
11. ![]()
Show Solution

12. ![]()
13. ![]()
Show Solution

14. ![]()
15. Find the linear speed of a point on the equator of the earth if the earth has a radius of 3,960 miles and the earth rotates on its axis every 24 hours. Express answer in miles per hour. Round to the nearest hundredth.
Show Solution
1036.73 miles per hour
16. A car wheel with a diameter of 18 inches spins at the rate of 10 revolutions per second. What is the car’s speed in miles per hour? Round to the nearest hundredth.
Right Triangle Trigonometry
For the following exercises, use side lengths to evaluate.
17. ![]()
Show Solution
![]()
18. ![]()
19. ![]()
Show Solution
![]()
18. ![]()
19. ![]()
Show Solution
![]()
For the following exercises, use the given information to find the lengths of the other two sides of the right triangle.
20. ![]()
21. ![]()
Show Solution
![]()
For the following exercises, use (Figure) to evaluate each trigonometric function.

22. ![]()
23. ![]()
Show Solution
![]()
For the following exercises, solve for the unknown sides of the given triangle.
24. 
25. 
Show Solution
![]()
26. A 15-ft ladder leans against a building so that the angle between the ground and the ladder is ![]() How high does the ladder reach up the side of the building? Find the answer to four decimal places.
How high does the ladder reach up the side of the building? Find the answer to four decimal places.
27. The angle of elevation to the top of a building in Baltimore is found to be 4 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building. Find the answer to four decimal places.
Show Solution
369.2136 ft
Unit Circle
28. Find the exact value of ![]()
29. Find the exact value of ![]()
Show Solution
![]()
30. Find the exact value of ![]()
31. State the reference angle for ![]()
Show Solution
![]()
32. State the reference angle for ![]()
33. Compute cosine of ![]()
Show Solution
![]()
34. Compute sine of ![]()
35. State the domain of the sine and cosine functions.
Show Solution
all real numbers
36. State the range of the sine and cosine functions.
The Other Trigonometric Functions
For the following exercises, find the exact value of the given expression.
37. ![]()
Show Solution
![]()
38. ![]()
39. ![]()
Show Solution
![]()
40. ![]()
For the following exercises, use reference angles to evaluate the given expression.
41. ![]()
Show Solution
2
42. ![]()
43. If ![]() what is the
what is the ![]()
Show Solution
–2.5
44. If ![]() what is the
what is the ![]()
45. If ![]() find
find ![]()
Show Solution
![]()
46. If ![]() find
find ![]()
47. Which trigonometric functions are even?
Show Solution
cosine, secant
48. Which trigonometric functions are odd?
Glossary
- cosecant
- the reciprocal of the sine function: on the unit circle,
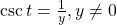
- cotangent
- the reciprocal of the tangent function: on the unit circle,
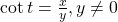
- identities
- statements that are true for all values of the input on which they are defined
- period
- the smallest interval
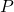 of a repeating function
of a repeating function 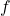 such that
such that 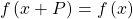
- secant
- the reciprocal of the cosine function: on the unit circle,
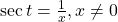
- tangent
- the quotient of the sine and cosine: on the unit circle,