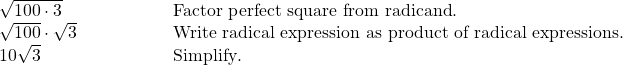Chapter 1.2: Radicals and Rational Exponents
Learning Objectives
In this section students will:
- Evaluate square roots.
- Use the product rule to simplify square roots.
- Use the quotient rule to simplify square roots.
- Add and subtract square roots.
- Rationalize denominators.
- Use rational roots.
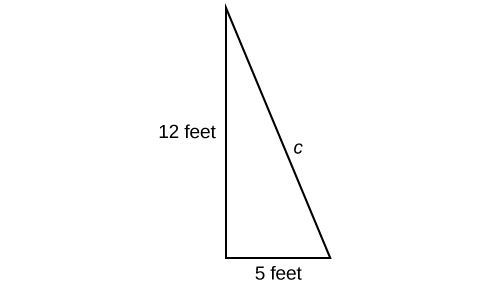
A hardware store sells 16-ft ladders and 24-ft ladders. A window is located 12 feet above the ground. A ladder needs to be purchased that will reach the window from a point on the ground 5 feet from the building. To find out the length of ladder needed, we can draw a right triangle as shown in (Figure), and use the Pythagorean Theorem.
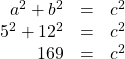
Evaluating Square Roots
When the square root of a number is squared, the result is the original number. Since ![]() the square root of
the square root of ![]() is
is ![]() The square root function is the inverse of the squaring function just as subtraction is the inverse of addition. To undo squaring, we take the square root.
The square root function is the inverse of the squaring function just as subtraction is the inverse of addition. To undo squaring, we take the square root.
In general terms, if ![]() is a positive real number, then the square root of
is a positive real number, then the square root of ![]() is a number that, when multiplied by itself, gives
is a number that, when multiplied by itself, gives ![]() The square root could be positive or negative because multiplying two negative numbers gives a positive number. The principal square root is the nonnegative number that when multiplied by itself equals
The square root could be positive or negative because multiplying two negative numbers gives a positive number. The principal square root is the nonnegative number that when multiplied by itself equals ![]() The square root obtained using a calculator is the principal square root.
The square root obtained using a calculator is the principal square root.
The principal square root of ![]() is written as
is written as ![]() The symbol is called a radical, the term under the symbol is called the radicand, and the entire expression is called a radical expression.
The symbol is called a radical, the term under the symbol is called the radicand, and the entire expression is called a radical expression.

Principal Square Root
The principal square root of ![]() is the nonnegative number that, when multiplied by itself, equals
is the nonnegative number that, when multiplied by itself, equals ![]() It is written as a radical expression, with a symbol called a radical over the term called the radicand:
It is written as a radical expression, with a symbol called a radical over the term called the radicand: ![]()
Does ![]()
No. Although both ![]() and
and ![]() are
are ![]() the radical symbol implies only a nonnegative root, the principal square root. The principal square root of 25 is
the radical symbol implies only a nonnegative root, the principal square root. The principal square root of 25 is ![]()
Evaluating Square Roots
Evaluate each expression.
Show Solution
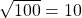 because
because 
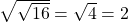 because
because 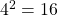 and
and 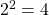
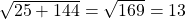 because
because 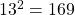
 because
because 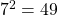 and
and 
For ![]() can we find the square roots before adding?
can we find the square roots before adding?
No. ![]() This is not equivalent to
This is not equivalent to ![]() The order of operations requires us to add the terms in the radicand before finding the square root.
The order of operations requires us to add the terms in the radicand before finding the square root.
Try It
Evaluate each expression.
Show Solution
Using the Product Rule to Simplify Square Roots
To simplify a square root, we rewrite it such that there are no perfect squares in the radicand. There are several properties of square roots that allow us to simplify complicated radical expressions. The first rule we will look at is the product rule for simplifying square roots, which allows us to separate the square root of a product of two numbers into the product of two separate rational expressions. For instance, we can rewrite ![]() as
as ![]() We can also use the product rule to express the product of multiple radical expressions as a single radical expression.
We can also use the product rule to express the product of multiple radical expressions as a single radical expression.
The Product Rule for Simplifying Square Roots
If ![]() and
and ![]() are nonnegative, the square root of the product
are nonnegative, the square root of the product ![]() is equal to the product of the square roots of
is equal to the product of the square roots of ![]() and
and ![]()
How To
Given a square root radical expression, use the product rule to simplify it.
- Factor any perfect squares from the radicand.
- Write the radical expression as a product of radical expressions.
- Simplify.
Using the Product Rule to Simplify Square Roots
Simplify the radical expression.
Show Solution
Try It
Simplify ![]()
Show Solution
![]() Notice the absolute value signs around x and y? That’s because their value must be positive!
Notice the absolute value signs around x and y? That’s because their value must be positive!
How To
Given the product of multiple radical expressions, use the product rule to combine them into one radical expression.
- Express the product of multiple radical expressions as a single radical expression.
- Simplify.
Using the Product Rule to Simplify the Product of Multiple Square Roots
Simplify the radical expression.
![]()
Show Solution
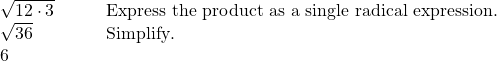
Try It
Simplify ![]() assuming
assuming ![]()
Show Solution
![]()
Using the Quotient Rule to Simplify Square Roots
Just as we can rewrite the square root of a product as a product of square roots, so too can we rewrite the square root of a quotient as a quotient of square roots, using the quotient rule for simplifying square roots. It can be helpful to separate the numerator and denominator of a fraction under a radical so that we can take their square roots separately. We can rewrite ![]() as
as ![]()
The Quotient Rule for Simplifying Square Roots
The square root of the quotient ![]() is equal to the quotient of the square roots of
is equal to the quotient of the square roots of ![]() and
and ![]() where
where ![]()
How To
Given a radical expression, use the quotient rule to simplify it.
- Write the radical expression as the quotient of two radical expressions.
- Simplify the numerator and denominator.
Using the Quotient Rule to Simplify Square Roots
Simplify the radical expression.
![]()
Show Solution

Try It
Simplify ![]()
Show Solution
![]() We do not need the absolute value signs for
We do not need the absolute value signs for ![]() because that term will always be nonnegative.
because that term will always be nonnegative.
Using the Quotient Rule to Simplify an Expression with Two Square Roots
Simplify the radical expression.
![]()
Show Solution

Try It
Simplify ![]()
Show Solution
![]()
Adding and Subtracting Square Roots
We can add or subtract radical expressions only when they have the same radicand and when they have the same radical type such as square roots. For example, the sum of ![]() and
and ![]() is
is ![]() However, it is often possible to simplify radical expressions, and that may change the radicand. The radical expression
However, it is often possible to simplify radical expressions, and that may change the radicand. The radical expression ![]() can be written with a
can be written with a ![]() in the radicand, as
in the radicand, as ![]() so
so ![]()
How To
Given a radical expression requiring addition or subtraction of square roots, solve.
- Simplify each radical expression.
- Add or subtract expressions with equal radicands.
Adding Square Roots
Add ![]()
Show Solution
We can rewrite ![]() as
as ![]() According the product rule, this becomes
According the product rule, this becomes ![]() The square root of
The square root of ![]() is 2, so the expression becomes
is 2, so the expression becomes ![]() which is
which is ![]() Now we can the terms have the same radicand so we can add.
Now we can the terms have the same radicand so we can add.
![]()
Try It
Add ![]()
Show Solution
![]()
Subtracting Square Roots
Subtract ![]()
Show Solution
Rewrite each term so they have equal radicands.
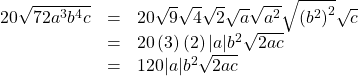
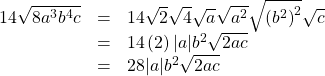
Now the terms have the same radicand so we can subtract.
Try It
Subtract ![]()
Show Solution
![]()
Rationalizing Denominators
When an expression involving square root radicals is written in simplest form, it will not contain a radical in the denominator. We can remove radicals from the denominators of fractions using a process called rationalizing the denominator.
We know that multiplying by 1 does not change the value of an expression. We use this property of multiplication to change expressions that contain radicals in the denominator. To remove radicals from the denominators of fractions, multiply by the form of 1 that will eliminate the radical.
For a denominator containing a single term, multiply by the radical in the denominator over itself. In other words, if the denominator is ![]() multiply by
multiply by ![]()
For a denominator containing the sum or difference of a rational and an irrational term, multiply the numerator and denominator by the conjugate of the denominator, which is found by changing the sign of the radical portion of the denominator. If the denominator is ![]() then the conjugate is
then the conjugate is ![]()
How To
Given an expression with a single square root radical term in the denominator, rationalize the denominator.
- Multiply the numerator and denominator by the radical in the denominator.
- Simplify.
Rationalizing a Denominator Containing a Single Term
Write ![]() in simplest form.
in simplest form.
Show Solution
The radical in the denominator is ![]() So multiply the fraction by
So multiply the fraction by ![]() Then simplify.
Then simplify.
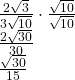
Try It
Write ![]() in simplest form.
in simplest form.
Show Solution
![]()
How To
Given an expression with a radical term and a constant in the denominator, rationalize the denominator.
- Find the conjugate of the denominator.
- Multiply the numerator and denominator by the conjugate.
- Use the distributive property.
- Simplify.
Rationalizing a Denominator Containing Two Terms
Write ![]() in simplest form.
in simplest form.
Show Solution
Begin by finding the conjugate of the denominator by writing the denominator and changing the sign. So the conjugate of ![]() is
is ![]() Then multiply the fraction by
Then multiply the fraction by ![]()

Try It
Write ![]() in simplest form.
in simplest form.
Show Solution
![]()
Using Rational Roots
Although square roots are the most common rational roots, we can also find cube roots, 4th roots, 5th roots, and more. Just as the square root function is the inverse of the squaring function, these roots are the inverse of their respective power functions. These functions can be useful when we need to determine the number that, when raised to a certain power, gives a certain number.
Understanding nth Roots
Suppose we know that ![]() We want to find what number raised to the 3rd power is equal to 8. Since
We want to find what number raised to the 3rd power is equal to 8. Since ![]() we say that 2 is the cube root of 8.
we say that 2 is the cube root of 8.
The nth root of ![]() is a number that, when raised to the nth power, gives
is a number that, when raised to the nth power, gives ![]() For example,
For example, ![]() is the 5th root of
is the 5th root of ![]() because
because ![]() If
If ![]() is a real number with at least one nth root, then the principal nth root of
is a real number with at least one nth root, then the principal nth root of ![]() is the number with the same sign as
is the number with the same sign as ![]() that, when raised to the nth power, equals
that, when raised to the nth power, equals ![]()
The principal nth root of ![]() is written as
is written as ![]() where
where ![]() is a positive integer greater than or equal to 2. In the radical expression,
is a positive integer greater than or equal to 2. In the radical expression, ![]() is called the index of the radical.
is called the index of the radical.
Principal nth Root
If ![]() is a real number with at least one nth root, then the principal nth root of
is a real number with at least one nth root, then the principal nth root of ![]() written as
written as ![]() is the number with the same sign as
is the number with the same sign as ![]() that, when raised to the nth power, equals
that, when raised to the nth power, equals ![]() The index of the radical is
The index of the radical is ![]()
Simplifying nth Roots
Simplify each of the following:
Show Solution
![Rendered by QuickLaTeX.com \sqrt[5]{-32}=-2\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1bd941055bc9c99565d2c15d75f845c4_l3.png) because
because 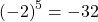
- First, express the product as a single radical expression.
![Rendered by QuickLaTeX.com \,\sqrt[4]{4,096}=8\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-69d9f526122017b2b001bf59ef761cb0_l3.png) because
because 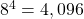
![Rendered by QuickLaTeX.com \begin{array}{cc}\frac{-\sqrt[3]{8{x}^{6}}}{\sqrt[3]{125}}\hfill & \phantom{\rule{3em}{0ex}}\text{Write as quotient of two radical expressions}.\hfill \\ \frac{-2{x}^{2}}{5}\hfill & \phantom{\rule{3em}{0ex}}\text{Simplify}.\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8248c88cbcf937e0bea26ec2675a1f73_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{cc}8\sqrt[4]{3}-2\sqrt[4]{3}\hfill & \phantom{\rule{2em}{0ex}}\text{Simplify to get equal radicands}.\hfill \\ 6\sqrt[4]{3} \hfill & \phantom{\rule{2em}{0ex}}\text{Add}.\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-90ea47bfcb50ee5c89fa13405ad7f76e_l3.png)
Try It
Simplify.
Show Solution
Using Rational Exponents
Radical expressions can also be written without using the radical symbol. We can use rational (fractional) exponents. The index must be a positive integer. If the index ![]() is even, then
is even, then ![]() cannot be negative.
cannot be negative.
We can also have rational exponents with numerators other than 1. In these cases, the exponent must be a fraction in lowest terms. We raise the base to a power and take an nth root. The numerator tells us the power and the denominator tells us the root.
All of the properties of exponents that we learned for integer exponents also hold for rational exponents.
Rational Exponents
Rational exponents are another way to express principal nth roots. The general form for converting between a radical expression with a radical symbol and one with a rational exponent is
How To
Given an expression with a rational exponent, write the expression as a radical.
- Determine the power by looking at the numerator of the exponent.
- Determine the root by looking at the denominator of the exponent.
- Using the base as the radicand, raise the radicand to the power and use the root as the index.
Writing Rational Exponents as Radicals
Write ![]() as a radical. Simplify.
as a radical. Simplify.
Show Solution
The 2 tells us the power and the 3 tells us the root.
![]()
We know that ![]() because
because ![]() Because the cube root is easy to find, it is easiest to find the cube root before squaring for this problem. In general, it is easier to find the root first and then raise it to a power.
Because the cube root is easy to find, it is easiest to find the cube root before squaring for this problem. In general, it is easier to find the root first and then raise it to a power.
![]()
Try It
Write ![]() as a radical. Simplify.
as a radical. Simplify.
Show Solution
![]()
Writing Radicals as Rational Exponents
Write ![]() using a rational exponent.
using a rational exponent.
Show Solution
The power is 2 and the root is 7, so the rational exponent will be ![]() We get
We get ![]() Using properties of exponents, we get
Using properties of exponents, we get ![]()
Try It
Write ![]() using a rational exponent.
using a rational exponent.
Show Solution
![]()
Simplifying Rational Exponents
Simplify:
Show Solution
Try It
Simplify ![]()
Show Solution
![]()
Access these online resources for additional instruction and practice with radicals and rational exponents.
Key Concepts
- The principal square root of a number
 is the nonnegative number that when multiplied by itself equals
is the nonnegative number that when multiplied by itself equals 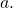 See (Figure).
See (Figure). - If
 and
and 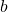 are nonnegative, the square root of the product
are nonnegative, the square root of the product 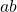 is equal to the product of the square roots of
is equal to the product of the square roots of  and
and 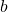 See (Figure) and (Figure).
See (Figure) and (Figure). - If
 and
and 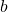 are nonnegative, the square root of the quotient
are nonnegative, the square root of the quotient 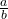 is equal to the quotient of the square roots of
is equal to the quotient of the square roots of  and
and 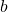 See (Figure) and (Figure).
See (Figure) and (Figure). - We can add and subtract radical expressions if they have the same radicand and the same index. See (Figure) and (Figure).
- Radical expressions written in simplest form do not contain a radical in the denominator. To eliminate the square root radical from the denominator, multiply both the numerator and the denominator by the conjugate of the denominator. See (Figure) and (Figure).
- The principal nth root of
 is the number with the same sign as
is the number with the same sign as  that when raised to the nth power equals
that when raised to the nth power equals 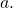 These roots have the same properties as square roots. See (Figure).
These roots have the same properties as square roots. See (Figure). - Radicals can be rewritten as rational exponents and rational exponents can be rewritten as radicals. See (Figure) and (Figure).
- The properties of exponents apply to rational exponents. See (Figure).
Section Exercises
Verbal
1. What does it mean when a radical does not have an index? Is the expression equal to the radicand? Explain.
Show Solution
When there is no index, it is assumed to be 2 or the square root. The expression would only be equal to the radicand if the index were 1.
2. Where would radicals come in the order of operations? Explain why.
3. Every number will have two square roots. What is the principal square root?
Show Solution
The principal square root is the nonnegative root of the number.
4. Can a radical with a negative radicand have a real square root? Why or why not?
Numeric
For the following exercises, simplify each expression.
5. ![]()
Show Solution
16
6. ![]()
7. ![]()
Show Solution
10
8. ![]()
9. ![]()
Show Solution
14
10. ![]()
11. ![]()
Show Solution
![]()
12. ![]()
13. ![]()
Show Solution
![]()
14. ![]()
15. ![]()
Show Solution
25
16. ![]()
17. ![]()
Show Solution
![]()
18. ![]()
19. ![]()
Show Solution
![]()
20. ![]()
21. ![]()
Show Solution
![]()
22. ![]()
23. ![]()
Show Solution
![]()
24. ![]()
25. ![]()
Show Solution
![]()
26. ![]()
27. ![]()
Show Solution
![]()
28. ![]()
29. ![]()
Show Solution
![]()
30. ![]()
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
![]()
34. ![]()
Algebraic
For the following exercises, simplify each expression.
35. ![]()
Show Solution
![]()
36. ![]()
37. ![]()
Show Solution
![]()
38. ![]()
39. ![]()
Show Solution
![]()
40. ![]()
41. ![]()
Show Solution
![]()
42. ![]()
43. ![]()
Show Solution
![]()
44. ![]()
45. ![]()
Show Solution
![]()
46. ![]()
47. ![]()
Show Solution
![]()
48. ![]()
49. ![]()
Show Solution
![]()
50. ![]()
51. ![]()
Show Solution
![]()
52. ![]()
53. ![]()
Show Solution
![]()
54. ![]()
55. ![]()
Show Solution
![]()
56. ![]()
57. ![]()
Show Solution
![]()
58. ![]()
59. ![]()
Show Solution
![]()
60. ![]()
61. ![]()
Show Solution
![]()
62. ![]()
63. ![]()
Show Solution
![]()
64. ![]()
Real-World Applications
65. A guy wire for a suspension bridge runs from the ground diagonally to the top of the closest pylon to make a triangle. We can use the Pythagorean Theorem to find the length of guy wire needed. The square of the distance between the wire on the ground and the pylon on the ground is 90,000 feet. The square of the height of the pylon is 160,000 feet. So the length of the guy wire can be found by evaluating ![]() What is the length of the guy wire?
What is the length of the guy wire?
Show Solution
500 feet
66. A car accelerates at a rate of ![]() where t is the time in seconds after the car moves from rest. Simplify the expression.
where t is the time in seconds after the car moves from rest. Simplify the expression.
Extensions
For the following exercises, simplify each expression.
67. ![]()
Show Solution
![]()
68. ![]()
69. ![]()
Show Solution
![]()
70. ![]()
71. ![]()
Show Solution
![]()
72. ![]()
73. ![]()
Show Solution
![]()
Glossary
- index
- the number above the radical sign indicating the nth root
- principal nth root
- the number with the same sign as
 that when raised to the nth power equals
that when raised to the nth power equals 
- principal square root
- the nonnegative square root of a number
 that, when multiplied by itself, equals
that, when multiplied by itself, equals 
- radical
- the symbol used to indicate a root
- radical expression
- an expression containing a radical symbol
- radicand
- the number under the radical symbol