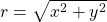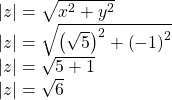Chapter 4.6: Polar Form of Complex Numbers
Learning Objectives
In this section, you will:
- Plot complex numbers in the complex plane.
- Find the absolute value of a complex number.
- Write complex numbers in polar form.
- Convert a complex number from polar to rectangular form.
- Find products of complex numbers in polar form.
- Find quotients of complex numbers in polar form.
- Find powers of complex numbers in polar form.
- Find roots of complex numbers in polar form.
“God made the integers; all else is the work of man.” This rather famous quote by nineteenth-century German mathematician Leopold Kronecker sets the stage for this section on the polar form of a complex number. Complex numbers were invented by people and represent over a thousand years of continuous investigation and struggle by mathematicians such as Pythagoras, Descartes, De Moivre, Euler, Gauss, and others. Complex numbers answered questions that for centuries had puzzled the greatest minds in science.
We first encountered complex numbers in Complex Numbers. In this section, we will focus on the mechanics of working with complex numbers: translation of complex numbers from polar form to rectangular form and vice versa, interpretation of complex numbers in the scheme of applications, and application of De Moivre’s Theorem.
Plotting Complex Numbers in the Complex Plane
Plotting a complex number ![]() is similar to plotting a real number, except that the horizontal axis represents the real part of the number,
is similar to plotting a real number, except that the horizontal axis represents the real part of the number, ![]() and the vertical axis represents the imaginary part of the number,
and the vertical axis represents the imaginary part of the number, ![]()
How To
Given a complex number ![]() plot it in the complex plane.
plot it in the complex plane.
- Label the horizontal axis as the real axis and the vertical axis as the imaginary axis.
- Plot the point in the complex plane by moving
 units in the horizontal direction and
units in the horizontal direction and 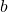 units in the vertical direction.
units in the vertical direction.
Plotting a Complex Number in the Complex Plane
Plot the complex number ![]() in the complex plane.
in the complex plane.
Show Solution
From the origin, move two units in the positive horizontal direction and three units in the negative vertical direction. See (Figure).

Try It
Plot the point ![]() in the complex plane.
in the complex plane.
Show Solution

Finding the Absolute Value of a Complex Number
The first step toward working with a complex number in polar form is to find the absolute value. The absolute value of a complex number is the same as its magnitude, or ![]() It measures the distance from the origin to a point in the plane. For example, the graph of
It measures the distance from the origin to a point in the plane. For example, the graph of ![]() in (Figure), shows
in (Figure), shows ![]()

Absolute Value of a Complex Number
Given ![]() a complex number, the absolute value of
a complex number, the absolute value of ![]() is defined as
is defined as
It is the distance from the origin to the point ![]()
Notice that the absolute value of a real number gives the distance of the number from 0, while the absolute value of a complex number gives the distance of the number from the origin, ![]()
Finding the Absolute Value of a Complex Number with a Radical
Find the absolute value of ![]()
Try It
Find the absolute value of the complex number ![]()
Show Solution
13
Finding the Absolute Value of a Complex Number
Given ![]() find
find ![]()
Try It
Given ![]() find
find ![]()
Show Solution
![]()
Writing Complex Numbers in Polar Form
The polar form of a complex number expresses a number in terms of an angle ![]() and its distance from the origin
and its distance from the origin ![]() Given a complex number in rectangular form expressed as
Given a complex number in rectangular form expressed as ![]() we use the same conversion formulas as we do to write the number in trigonometric form:
we use the same conversion formulas as we do to write the number in trigonometric form:
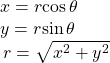
We review these relationships in (Figure).

We use the term modulus to represent the absolute value of a complex number, or the distance from the origin to the point ![]() The modulus, then, is the same as
The modulus, then, is the same as ![]() the radius in polar form. We use
the radius in polar form. We use ![]() to indicate the angle of direction (just as with polar coordinates). Substituting, we have
to indicate the angle of direction (just as with polar coordinates). Substituting, we have
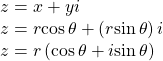
Polar Form of a Complex Number
Writing a complex number in polar form involves the following conversion formulas:
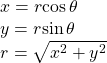
Making a direct substitution, we have
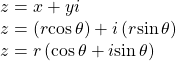
where ![]() is the modulus and
is the modulus and ![]() is the argument. We often use the abbreviation
is the argument. We often use the abbreviation ![]() to represent
to represent ![]()
Expressing a Complex Number Using Polar Coordinates
Express the complex number ![]() using polar coordinates.
using polar coordinates.
Show Solution
On the complex plane, the number ![]() is the same as
is the same as ![]() Writing it in polar form, we have to calculate
Writing it in polar form, we have to calculate ![]() first.
first.
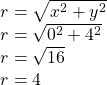
Next, we look at ![]() If
If ![]() and
and ![]() then
then ![]() In polar coordinates, the complex number
In polar coordinates, the complex number ![]() can be written as
can be written as ![]() or
or ![]() See (Figure).
See (Figure).

Try It
Express ![]() as
as ![]() in polar form.
in polar form.
Show Solution
![]()
Finding the Polar Form of a Complex Number
Find the polar form of ![]()
Show Solution
First, find the value of ![]()
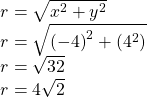
Find the angle ![]() using the formula:
using the formula:
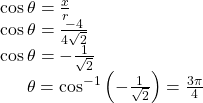
Thus, the solution is ![]()
Try It
Write ![]() in polar form.
in polar form.
Show Solution
![]()
Converting a Complex Number from Polar to Rectangular Form
Converting a complex number from polar form to rectangular form is a matter of evaluating what is given and using the distributive property. In other words, given ![]() first evaluate the trigonometric functions
first evaluate the trigonometric functions ![]() and
and ![]() Then, multiply through by
Then, multiply through by ![]()
Converting from Polar to Rectangular Form
Convert the polar form of the given complex number to rectangular form:
Show Solution
We begin by evaluating the trigonometric expressions.
After substitution, the complex number is
We apply the distributive property:
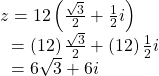
The rectangular form of the given point in complex form is ![]()
Finding the Rectangular Form of a Complex Number
Find the rectangular form of the complex number given ![]() and
and ![]()
Show Solution
If ![]() and
and ![]() we first determine
we first determine ![]() We then find
We then find ![]() and
and ![]()
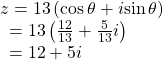
The rectangular form of the given number in complex form is ![]()
Try It
Convert the complex number to rectangular form:
Show Solution
![]()
Finding Products of Complex Numbers in Polar Form
Now that we can convert complex numbers to polar form we will learn how to perform operations on complex numbers in polar form. For the rest of this section, we will work with formulas developed by French mathematician Abraham de Moivre (1667-1754). These formulas have made working with products, quotients, powers, and roots of complex numbers much simpler than they appear. The rules are based on multiplying the moduli and adding the arguments.
Products of Complex Numbers in Polar Form
If ![]() and
and ![]() then the product of these numbers is given as:
then the product of these numbers is given as:
Notice that the product calls for multiplying the moduli and adding the angles.
Finding the Product of Two Complex Numbers in Polar Form
Find the product of ![]() given
given ![]() and
and ![]()
Show Solution
Follow the formula
![Rendered by QuickLaTeX.com \begin{array}{l}{z}_{1}{z}_{2}=4\cdot 2\left[\mathrm{cos}\left(80°+145°\right)+i\mathrm{sin}\left(80°+145°\right)\right]\hfill \\ {z}_{1}{z}_{2}=8\left[\mathrm{cos}\left(225°\right)+i\mathrm{sin}\left(225°\right)\right]\hfill \\ {z}_{1}{z}_{2}=8\left[\mathrm{cos}\left(\frac{5\pi }{4}\right)+i\mathrm{sin}\left(\frac{5\pi }{4}\right)\right]\hfill \\ {z}_{1}{z}_{2}=8\left[-\frac{\sqrt{2}}{2}+i\left(-\frac{\sqrt{2}}{2}\right)\right]\hfill \\ {z}_{1}{z}_{2}=-4\sqrt{2}-4i\sqrt{2}\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f5772439534d96fe1d56599313f93f58_l3.png)
Finding Quotients of Complex Numbers in Polar Form
The quotient of two complex numbers in polar form is the quotient of the two moduli and the difference of the two arguments.
Quotients of Complex Numbers in Polar Form
If ![]() and
and ![]() then the quotient of these numbers is
then the quotient of these numbers is
Notice that the moduli are divided, and the angles are subtracted.
How To
Given two complex numbers in polar form, find the quotient.
- Divide
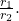
- Find
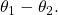
- Substitute the results into the formula:
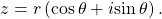 Replace
Replace  with
with 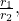 and replace
and replace 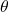 with
with 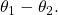
- Calculate the new trigonometric expressions and multiply through by
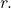
Finding the Quotient of Two Complex Numbers
Find the quotient of ![]() and
and ![]()
Show Solution
Using the formula, we have
![Rendered by QuickLaTeX.com \begin{array}{l}\frac{{z}_{1}}{{z}_{2}}=\frac{2}{4}\left[\mathrm{cos}\left(213°-33°\right)+i\mathrm{sin}\left(213°-33°\right)\right]\hfill \\ \frac{{z}_{1}}{{z}_{2}}=\frac{1}{2}\left[\mathrm{cos}\left(180°\right)+i\mathrm{sin}\left(180°\right)\right]\hfill \\ \frac{{z}_{1}}{{z}_{2}}=\frac{1}{2}\left[-1+0i\right]\hfill \\ \frac{{z}_{1}}{{z}_{2}}=-\frac{1}{2}+0i\hfill \\ \frac{{z}_{1}}{{z}_{2}}=-\frac{1}{2}\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a2242d0884e1ea9462f6b0116d6074f0_l3.png)
Try It
Find the product and the quotient of ![]() and
and ![]()
Show Solution
![]()
Finding Powers of Complex Numbers in Polar Form
Finding powers of complex numbers is greatly simplified using De Moivre’s Theorem. It states that, for a positive integer ![]() is found by raising the modulus to the
is found by raising the modulus to the ![]() power and multiplying the argument by
power and multiplying the argument by ![]() It is the standard method used in modern mathematics.
It is the standard method used in modern mathematics.
De Moivre’s Theorem
If ![]() is a complex number, then
is a complex number, then
where ![]()
is a positive integer.
Evaluating an Expression Using De Moivre’s Theorem
Evaluate the expression ![]() using De Moivre’s Theorem.
using De Moivre’s Theorem.
Show Solution
Since De Moivre’s Theorem applies to complex numbers written in polar form, we must first write ![]() in polar form. Let us find
in polar form. Let us find ![]()
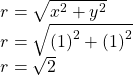
Then we find ![]() Using the formula
Using the formula ![]() gives
gives
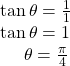
Use De Moivre’s Theorem to evaluate the expression.
![Rendered by QuickLaTeX.com \begin{array}{l}{\left(a+bi\right)}^{n}={r}^{n}\left[\mathrm{cos}\left(n\theta \right)+i\mathrm{sin}\left(n\theta \right)\right]\hfill \\ \,\,\,\,{\left(1+i\right)}^{5}={\left(\sqrt{2}\right)}^{5}\left[\mathrm{cos}\left(5\cdot \frac{\pi }{4}\right)+i\mathrm{sin}\left(5\cdot \frac{\pi }{4}\right)\right]\hfill \\ \,\,\,\,{\left(1+i\right)}^{5}=4\sqrt{2}\left[\mathrm{cos}\left(\frac{5\pi }{4}\right)+i\mathrm{sin}\left(\frac{5\pi }{4}\right)\right]\hfill \\ \,\,\,\,{\left(1+i\right)}^{5}=4\sqrt{2}\left[-\frac{\sqrt{2}}{2}+i\left(-\frac{\sqrt{2}}{2}\right)\right]\hfill \\ \,\,\,\,{\left(1+i\right)}^{5}=-4-4i\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-dddc93685204127efd402130aa55a608_l3.png)
Finding Roots of Complex Numbers in Polar Form
To find the nth root of a complex number in polar form, we use the ![]() Root Theorem or De Moivre’s Theorem and raise the complex number to a power with a rational exponent. There are several ways to represent a formula for finding
Root Theorem or De Moivre’s Theorem and raise the complex number to a power with a rational exponent. There are several ways to represent a formula for finding ![]() roots of complex numbers in polar form.
roots of complex numbers in polar form.
The nth Root Theorem
To find the ![]() root of a complex number in polar form, use the formula given as
root of a complex number in polar form, use the formula given as
where ![]() We add
We add ![]() to
to ![]() in order to obtain the periodic roots.
in order to obtain the periodic roots.
Finding the nth Root of a Complex Number
Evaluate the cube roots of ![]()
Show Solution
We have
![Rendered by QuickLaTeX.com \begin{array}{l}{z}^{\frac{1}{3}}={8}^{\frac{1}{3}}\left[\mathrm{cos}\left(\frac{\frac{2\pi }{3}}{3}+\frac{2k\pi }{3}\right)+i\mathrm{sin}\left(\frac{\frac{2\pi }{3}}{3}+\frac{2k\pi }{3}\right)\right]\hfill \\ {z}^{\frac{1}{3}}=2\left[\mathrm{cos}\left(\frac{2\pi }{9}+\frac{2k\pi }{3}\right)+i\mathrm{sin}\left(\frac{2\pi }{9}+\frac{2k\pi }{3}\right)\right]\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-00d1df4cc006a27e57eb9a781dacb439_l3.png)
There will be three roots: ![]() When
When ![]() we have
we have
When ![]() we have
we have
![Rendered by QuickLaTeX.com \begin{array}{l}{z}^{\frac{1}{3}}=2\left[\mathrm{cos}\left(\frac{2\pi }{9}+\frac{6\pi }{9}\right)+i\mathrm{sin}\left(\frac{2\pi }{9}+\frac{6\pi }{9}\right)\right]\begin{array}{cccc}& & & \end{array}\text{ Add }\frac{2\left(1\right)\pi }{3}\text{ to each angle.}\hfill \\ {z}^{\frac{1}{3}}=2\left(\mathrm{cos}\left(\frac{8\pi }{9}\right)+i\mathrm{sin}\left(\frac{8\pi }{9}\right)\right)\hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8206cf606dd29c504be993bd661cf2df_l3.png)
When ![]() we have
we have
![Rendered by QuickLaTeX.com \begin{array}{ll}{z}^{\frac{1}{3}}=2\left[\mathrm{cos}\left(\frac{2\pi }{9}+\frac{12\pi }{9}\right)+i\mathrm{sin}\left(\frac{2\pi }{9}+\frac{12\pi }{9}\right)\right]\begin{array}{cccc}& & & \end{array}\hfill & \text{Add }\frac{2\left(2\right)\pi }{3}\text{ to each angle.}\hfill \\ {z}^{\frac{1}{3}}=2\left(\mathrm{cos}\left(\frac{14\pi }{9}\right)+i\mathrm{sin}\left(\frac{14\pi }{9}\right)\right)\hfill & \hfill \end{array}](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e6276c97566af0e0796d06df08372964_l3.png)
Remember to find the common denominator to simplify fractions in situations like this one. For ![]() the angle simplification is
the angle simplification is
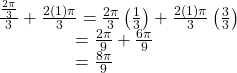
Try It
Find the four fourth roots of ![]()
Show Solution
![]()
![]()
![]()
![]()
Access these online resources for additional instruction and practice with polar forms of complex numbers.
Key Concepts
- Complex numbers in the form
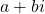 are plotted in the complex plane similar to the way rectangular coordinates are plotted in the rectangular plane. Label the x-axis as the real axis and the y-axis as the imaginary axis. See (Figure).
are plotted in the complex plane similar to the way rectangular coordinates are plotted in the rectangular plane. Label the x-axis as the real axis and the y-axis as the imaginary axis. See (Figure). - The absolute value of a complex number is the same as its magnitude. It is the distance from the origin to the point:
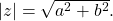 See (Figure) and (Figure).
See (Figure) and (Figure). - To write complex numbers in polar form, we use the formulas
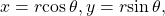 and
and 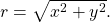 Then,
Then, 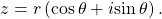 See (Figure) and (Figure).
See (Figure) and (Figure). - To convert from polar form to rectangular form, first evaluate the trigonometric functions. Then, multiply through by
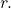 See (Figure) and (Figure).
See (Figure) and (Figure). - To find the product of two complex numbers, multiply the two moduli and add the two angles. Evaluate the trigonometric functions, and multiply using the distributive property. See (Figure).
- To find the quotient of two complex numbers in polar form, find the quotient of the two moduli and the difference of the two angles. See (Figure).
- To find the power of a complex number
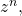 raise
raise  to the power
to the power 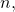 and multiply
and multiply 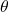 by
by 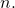 See (Figure).
See (Figure). - Finding the roots of a complex number is the same as raising a complex number to a power, but using a rational exponent. See (Figure).
Section Exercises
Verbal
1. A complex number is ![]() Explain each part.
Explain each part.
Show Solution
a is the real part, b is the imaginary part, and ![]()
2. What does the absolute value of a complex number represent?
3. How is a complex number converted to polar form?
Show Solution
Polar form converts the real and imaginary part of the complex number in polar form using ![]() and
and ![]()
4. How do we find the product of two complex numbers?
5. What is De Moivre’s Theorem and what is it used for?
Show Solution
![]() It is used to simplify polar form when a number has been raised to a power.
It is used to simplify polar form when a number has been raised to a power.
Algebraic
For the following exercises, find the absolute value of the given complex number.
6. ![]()
7. ![]()
Show Solution
![]()
8. ![]()
9. ![]()
Show Solution
![]()
10. ![]()
11. ![]()
Show Solution
![]()
For the following exercises, write the complex number in polar form.
12. ![]()
13. ![]()
Show Solution
![]()
14. ![]()
15. ![]()
Show Solution
![]()
16. ![]()
For the following exercises, convert the complex number from polar to rectangular form.
17. ![]()
Show Solution
![]()
18. ![]()
19. ![]()
Show Solution
![]()
20. ![]()
21. ![]()
Show Solution
![]()
22. ![]()
For the following exercises, find ![]() in polar form.
in polar form.
23. ![]()
Show Solution
![]()
24. ![]()
Show Solution
![]()
26. ![]()
27. ![]()
Show Solution
![]()
28. ![]()
For the following exercises, find ![]() in polar form.
in polar form.
29. ![]()
Show Solution
![]()
30. ![]()
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
![]()
34. ![]()
For the following exercises, find the powers of each complex number in polar form.
35. Find ![]() when
when ![]()
Show Solution
![]()
36. Find ![]() when
when ![]()
37. Find ![]() when
when ![]()
Show Solution
![]()
38. Find ![]() when
when ![]()
39. Find ![]() when
when ![]()
Show Solution
![]()
40. Find ![]() when
when ![]()
For the following exercises, evaluate each root.
41. Evaluate the cube root of ![]() when
when ![]()
Show Solution
![]()
42. Evaluate the square root of ![]() when
when ![]()
43. Evaluate the cube root of ![]() when
when ![]()
Show Solution
![]()
44. Evaluate the square root of ![]() when
when ![]()
45. Evaluate the cube root of ![]() when
when ![]()
Show Solution
![]()
Graphical
For the following exercises, plot the complex number in the complex plane.
46. ![]()
47. ![]()
Show Solution

48. ![]()
49. ![]()
Show Solution

50. ![]()
51. ![]()
Show Solution

52. ![]()
Show Solution

54. ![]()
55. ![]()
Show Solution

Technology
For the following exercises, find all answers rounded to the nearest hundredth.
56. Use the rectangular to polar feature on the graphing calculator to change ![]() to polar form.
to polar form.
57. Use the rectangular to polar feature on the graphing calculator to change ![]()
to polar form.
Show Solution
![]()
58. Use the rectangular to polar feature on the graphing calculator to change ![]()
to polar form.
59. Use the polar to rectangular feature on the graphing calculator to change ![]() to rectangular form.
to rectangular form.
Show Solution
![]()
60. Use the polar to rectangular feature on the graphing calculator to change ![]() to rectangular form.
to rectangular form.
61. Use the polar to rectangular feature on the graphing calculator to change ![]() to rectangular form.
to rectangular form.
Show Solution
![]()
Glossary
- argument
- the angle associated with a complex number; the angle between the line from the origin to the point and the positive real axis
- De Moivre’s Theorem
- formula used to find the
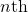 power or nth roots of a complex number; states that, for a positive integer
power or nth roots of a complex number; states that, for a positive integer 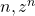 is found by raising the modulus to the
is found by raising the modulus to the 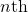 power and multiplying the angles by
power and multiplying the angles by 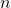
- modulus
- the absolute value of a complex number, or the distance from the origin to the point
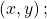 also called the amplitude
also called the amplitude
- polar form of a complex number
- a complex number expressed in terms of an angle
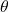 and its distance from the origin
and its distance from the origin 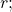 can be found by using conversion formulas
can be found by using conversion formulas 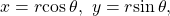 and
and