Chapter 7.4: Inverse Trigonometric Functions
Learning Objectives
In this section, you will:
- Understand and use the inverse sine, cosine, and tangent functions.
- Find the exact value of expressions involving the inverse sine, cosine, and tangent functions.
- Use a calculator to evaluate inverse trigonometric functions.
- Find exact values of composite functions with inverse trigonometric functions.
For any right triangle, given one other angle and the length of one side, we can figure out what the other angles and sides are. But what if we are given only two sides of a right triangle? We need a procedure that leads us from a ratio of sides to an angle. This is where the notion of an inverse to a trigonometric function comes into play. In this section, we will explore the inverse trigonometric functions.
Understanding and Using the Inverse Sine, Cosine, and Tangent Functions
In order to use inverse trigonometric functions, we need to understand that an inverse trigonometric function “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in (Figure).

For example, if ![]() then we would write
then we would write ![]() Be aware that
Be aware that ![]() does not mean
does not mean ![]() The following examples illustrate the inverse trigonometric functions:
The following examples illustrate the inverse trigonometric functions:
- Since
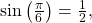 then
then 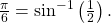
- Since
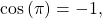 then
then 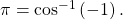
- Since
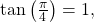 then
then 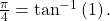
In previous sections, we evaluated the trigonometric functions at various angles, but at times we need to know what angle would yield a specific sine, cosine, or tangent value. For this, we need inverse functions. Recall that, for a one-to-one function, if ![]() then an inverse function would satisfy
then an inverse function would satisfy ![]()
Bear in mind that the sine, cosine, and tangent functions are not one-to-one functions. The graph of each function would fail the horizontal line test. In fact, no periodic function can be one-to-one because each output in its range corresponds to at least one input in every period, and there are an infinite number of periods. As with other functions that are not one-to-one, we will need to restrict the domain of each function to yield a new function that is one-to-one. We choose a domain for each function that includes the number 0. (Figure) shows the graph of the sine function limited to ![]() and the graph of the cosine function limited to
and the graph of the cosine function limited to ![]()

![Rendered by QuickLaTeX.com \,\left[-\frac{\pi }{2},\frac{\pi }{2}\right];\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fdcdc3147d8c08150cf3c4a7b3bd8faa_l3.png) (b) Cosine function on a restricted domain of
(b) Cosine function on a restricted domain of ![Rendered by QuickLaTeX.com \,\left[0,\pi \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-188fbcd6333be8919f371865783783d6_l3.png)
(Figure) shows the graph of the tangent function limited to ![]()

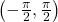
These conventional choices for the restricted domain are somewhat arbitrary, but they have important, helpful characteristics. Each domain includes the origin and some positive values, and most importantly, each results in a one-to-one function that is invertible. The conventional choice for the restricted domain of the tangent function also has the useful property that it extends from one vertical asymptote to the next instead of being divided into two parts by an asymptote.
On these restricted domains, we can define the inverse trigonometric functions.
- The inverse sine function
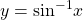 means
means 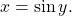 The inverse sine function is sometimes called the arcsine function, and notated
The inverse sine function is sometimes called the arcsine function, and notated 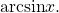
![Rendered by QuickLaTeX.com y={\mathrm{sin}}^{-1}x\,\text{has domain}\,\left[-1,1\right]\,\text{and range}\,\left[-\frac{\pi }{2},\frac{\pi }{2}\right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-396e9c87599f3ffbd96a7a590161c9cd_l3.png)
- The inverse cosine function
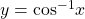 means
means 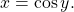 The inverse cosine function is sometimes called the arccosine function, and notated
The inverse cosine function is sometimes called the arccosine function, and notated 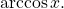
![Rendered by QuickLaTeX.com y={\mathrm{cos}}^{-1}x\,\text{has domain}\,\left[-1,1\right]\,\text{and range}\,\left[0,\pi \right]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-50df13525a79fdaeebbc544a33395ef5_l3.png)
- The inverse tangent function
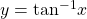 means
means 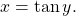 The inverse tangent function is sometimes called the arctangent function, and notated
The inverse tangent function is sometimes called the arctangent function, and notated 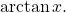
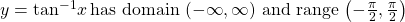
The graphs of the inverse functions are shown in (Figure), (Figure), and (Figure). Notice that the output of each of these inverse functions is a number, an angle in radian measure. We see that ![]() has domain
has domain ![]() and range
and range ![]()
![]() has domain
has domain ![]() and range
and range ![]() and
and ![]() has domain of all real numbers and range
has domain of all real numbers and range ![]() To find the domain and range of inverse trigonometric functions, switch the domain and range of the original functions. Each graph of the inverse trigonometric function is a reflection of the graph of the original function about the line
To find the domain and range of inverse trigonometric functions, switch the domain and range of the original functions. Each graph of the inverse trigonometric function is a reflection of the graph of the original function about the line ![]()



Relations for Inverse Sine, Cosine, and Tangent Functions
For angles in the interval ![]() if
if ![]() then
then ![]()
For angles in the interval ![]() if
if ![]() then
then ![]()
For angles in the interval ![]() if
if ![]() then
then ![]()
Writing a Relation for an Inverse Function
Given ![]() write a relation involving the inverse sine.
write a relation involving the inverse sine.
Show Solution
Use the relation for the inverse sine. If ![]() then
then ![]() .
.
In this problem, ![]() and
and ![]()
Try It
Given ![]() write a relation involving the inverse cosine.
write a relation involving the inverse cosine.
Show Solution
![]()
Finding the Exact Value of Expressions Involving the Inverse Sine, Cosine, and Tangent Functions
Now that we can identify inverse functions, we will learn to evaluate them. For most values in their domains, we must evaluate the inverse trigonometric functions by using a calculator, interpolating from a table, or using some other numerical technique. Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically ![]() (30°),
(30°), ![]() (45°), and
(45°), and ![]() (60°), and their reflections into other quadrants.
(60°), and their reflections into other quadrants.
How To
Given a “special” input value, evaluate an inverse trigonometric function.
- Find angle
 for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function.
for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function. - If
 is not in the defined range of the inverse, find another angle
is not in the defined range of the inverse, find another angle  that is in the defined range and has the same sine, cosine, or tangent as
that is in the defined range and has the same sine, cosine, or tangent as 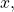 depending on which corresponds to the given inverse function.
depending on which corresponds to the given inverse function.
Evaluating Inverse Trigonometric Functions for Special Input Values
Evaluate each of the following.
Show Solution
- Evaluating
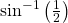 is the same as determining the angle that would have a sine value of
is the same as determining the angle that would have a sine value of 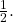 In other words, what angle
In other words, what angle 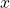 would satisfy
would satisfy 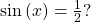 There are multiple values that would satisfy this relationship, such as
There are multiple values that would satisfy this relationship, such as 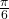 and
and 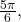 but we know we need the angle in the interval
but we know we need the angle in the interval ![Rendered by QuickLaTeX.com \,\left[-\frac{\pi }{2},\frac{\pi }{2}\right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-825cbbd3c7e6386f0af93e432c295956_l3.png) so the answer will be
so the answer will be 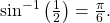 Remember that the inverse is a function, so for each input, we will get exactly one output.
Remember that the inverse is a function, so for each input, we will get exactly one output. - To evaluate
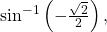 we know that
we know that 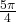 and
and 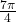 both have a sine value of
both have a sine value of 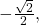 but neither is in the interval
but neither is in the interval ![Rendered by QuickLaTeX.com \,\left[-\frac{\pi }{2},\frac{\pi }{2}\right].\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-13dfda390d312ac043b18592e3039a4a_l3.png) For that, we need the negative angle coterminal with
For that, we need the negative angle coterminal with 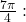
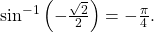
- To evaluate
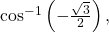 we are looking for an angle in the interval
we are looking for an angle in the interval ![Rendered by QuickLaTeX.com \,\left[0,\pi \right]\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-de56ce7251c5fd20eb24ef4b52ef6a13_l3.png) with a cosine value of
with a cosine value of 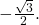 The angle that satisfies this is
The angle that satisfies this is 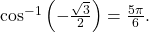
- Evaluating
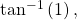 we are looking for an angle in the interval
we are looking for an angle in the interval 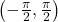 with a tangent value of 1. The correct angle is
with a tangent value of 1. The correct angle is 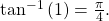
Try It
Evaluate each of the following.
Show Solution
a. ![]() b.
b. ![]() c.
c. ![]() d.
d. ![]()
Using a Calculator to Evaluate Inverse Trigonometric Functions
To evaluate inverse trigonometric functions that do not involve the special angles discussed previously, we will need to use a calculator or other type of technology. Most scientific calculators and calculator-emulating applications have specific keys or buttons for the inverse sine, cosine, and tangent functions. These may be labeled, for example, SIN
![]() , ARCSIN, or ASIN.
, ARCSIN, or ASIN.
In the previous chapter, we worked with trigonometry on a right triangle to solve for the sides of a triangle given one side and an additional angle. Using the inverse trigonometric functions, we can solve for the angles of a right triangle given two sides, and we can use a calculator to find the values to several decimal places.
In these examples and exercises, the answers will be interpreted as angles and we will use ![]() as the independent variable. The value displayed on the calculator may be in degrees or radians, so be sure to set the mode appropriate to the application.
as the independent variable. The value displayed on the calculator may be in degrees or radians, so be sure to set the mode appropriate to the application.
Evaluating the Inverse Sine on a Calculator
Evaluate ![]() using a calculator.
using a calculator.
Show Solution
Because the output of the inverse function is an angle, the calculator will give us a degree value if in degree mode and a radian value if in radian mode. Calculators also use the same domain restrictions on the angles as we are using.
In radian mode, ![]() In degree mode,
In degree mode, ![]() Note that in calculus and beyond we will use radians in almost all cases.
Note that in calculus and beyond we will use radians in almost all cases.
Try It
Evaluate ![]() using a calculator.
using a calculator.
Show Solution
1.9823 or 113.578°
How To
Given two sides of a right triangle like the one shown in (Figure), find an angle.

- If one given side is the hypotenuse of length
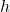 and the side of length
and the side of length  adjacent to the desired angle is given, use the equation
adjacent to the desired angle is given, use the equation 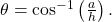
- If one given side is the hypotenuse of length
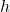 and the side of length
and the side of length 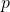 opposite to the desired angle is given, use the equation
opposite to the desired angle is given, use the equation 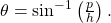
- If the two legs (the sides adjacent to the right angle) are given, then use the equation
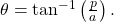
Applying the Inverse Cosine to a Right Triangle
Solve the triangle in (Figure) for the angle ![]()

Show Solution
Because we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.

Try It
Solve the triangle in (Figure) for the angle ![]()

Show Solution
![]() radians
radians
Finding Exact Values of Composite Functions with Inverse Trigonometric Functions
There are times when we need to compose a trigonometric function with an inverse trigonometric function. In these cases, we can usually find exact values for the resulting expressions without resorting to a calculator. Even when the input to the composite function is a variable or an expression, we can often find an expression for the output. To help sort out different cases, let ![]() and
and ![]() be two different trigonometric functions belonging to the set
be two different trigonometric functions belonging to the set ![]() and let
and let ![]() and
and ![]() be their inverses.
be their inverses.
Evaluating Compositions of the Form f(f−1(y)) and f−1(f(x))
For any trigonometric function, ![]() for all
for all ![]() in the proper domain for the given function. This follows from the definition of the inverse and from the fact that the range of
in the proper domain for the given function. This follows from the definition of the inverse and from the fact that the range of ![]() was defined to be identical to the domain of
was defined to be identical to the domain of ![]() However, we have to be a little more careful with expressions of the form
However, we have to be a little more careful with expressions of the form ![]()
Compositions of a trigonometric function and its inverse
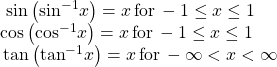
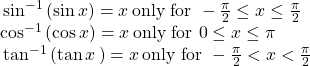
Is it correct that ![]()
No. This equation is correct if ![]() belongs to the restricted domain
belongs to the restricted domain ![]() but sine is defined for all real input values, and for
but sine is defined for all real input values, and for ![]() outside the restricted interval, the equation is not correct because its inverse always returns a value in
outside the restricted interval, the equation is not correct because its inverse always returns a value in ![]() The situation is similar for cosine and tangent and their inverses. For example,
The situation is similar for cosine and tangent and their inverses. For example, ![]()
Given an expression of the form f−1(f(θ)) where ![]() evaluate.
evaluate.
- If
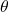 is in the restricted domain of
is in the restricted domain of 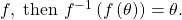
- If not, then find an angle
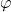 within the restricted domain of
within the restricted domain of 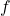 such that
such that 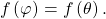 Then
Then 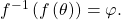
Using Inverse Trigonometric Functions
Evaluate the following:
Show Solution
![Rendered by QuickLaTeX.com \frac{\pi }{3}\text{ is in }\left[-\frac{\pi }{2},\frac{\pi }{2}\right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-282977869beec97ee3b8e50f6da6b17e_l3.png) so
so 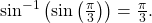
![Rendered by QuickLaTeX.com \frac{2\pi }{3}\text{ is not in }\left[-\frac{\pi }{2},\frac{\pi }{2}\right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-eebb071d05fcb878b616e628000d3530_l3.png) but
but 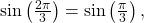 so
so 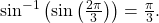
![Rendered by QuickLaTeX.com \frac{2\pi }{3}\text{ is in }\left[0,\pi \right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9406541a2e1533a1d069deee2d08e91f_l3.png) so
so 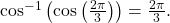
![Rendered by QuickLaTeX.com -\frac{\pi }{3}\text{ is not in }\left[0,\pi \right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3f26704711895f682e4fe62be628985b_l3.png) but
but 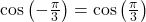 because cosine is an even function.
because cosine is an even function.![Rendered by QuickLaTeX.com \frac{\pi }{3}\text{ is in }\left[0,\pi \right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f567dfc06f405edd3106f627241efc1b_l3.png) so
so 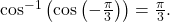
Try It
Evaluate ![]()
Show Solution
![]()
Evaluating Compositions of the Form f−1(g(x))
Now that we can compose a trigonometric function with its inverse, we can explore how to evaluate a composition of a trigonometric function and the inverse of another trigonometric function. We will begin with compositions of the form ![]() For special values of
For special values of ![]() we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is
we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is ![]() making the other
making the other ![]() Consider the sine and cosine of each angle of the right triangle in (Figure).
Consider the sine and cosine of each angle of the right triangle in (Figure).

Because ![]() we have
we have ![]() if
if ![]() If
If ![]() is not in this domain, then we need to find another angle that has the same cosine as
is not in this domain, then we need to find another angle that has the same cosine as ![]() and does belong to the restricted domain; we then subtract this angle from
and does belong to the restricted domain; we then subtract this angle from ![]() Similarly,
Similarly, ![]() so
so ![]() if
if ![]() These are just the function-cofunction relationships presented in another way.
These are just the function-cofunction relationships presented in another way.
Given functions of the form ![]() and
and ![]() evaluate them.
evaluate them.
- If
![Rendered by QuickLaTeX.com \,x\text{ is in }\left[0,\pi \right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e5263a6edc967fc9f516a2ecdd044810_l3.png) then
then 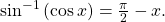
- If
![Rendered by QuickLaTeX.com \,x\text{ is not in }\left[0,\pi \right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e9fa82a1af8479f21f3b8984070285d7_l3.png) then find another angle
then find another angle ![Rendered by QuickLaTeX.com \,y\text{ in }\left[0,\pi \right]\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6abeb6c4442efe6728099fdddfb24624_l3.png) such that
such that 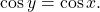
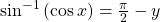
- If
![Rendered by QuickLaTeX.com \,x\text{ is in }\left[-\frac{\pi }{2},\frac{\pi }{2}\right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ca7700091fe9f5337cc4aa06f8760c5f_l3.png) then
then 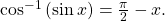
- If
![Rendered by QuickLaTeX.com \,x\text{ is not in}\,\left[-\frac{\pi }{2},\frac{\pi }{2}\right],\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0c467e44ca1bc92a3ad9380cd6806181_l3.png) then find another angle
then find another angle ![Rendered by QuickLaTeX.com \,y\text{ in }\left[-\frac{\pi }{2},\frac{\pi }{2}\right]\,](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f0c7b87126bbee6a6c861c95eec70f89_l3.png) such that
such that 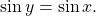
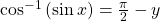
Evaluating the Composition of an Inverse Sine with a Cosine
Evaluate ![]()
- by direct evaluation.
- by the method described previously.
Show Solution
- Here, we can directly evaluate the inside of the composition.
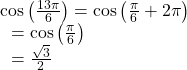
Now, we can evaluate the inverse function as we did earlier.
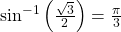
- We have
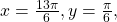 and
and
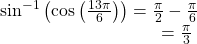
Try It
Evaluate ![]()
Show Solution
![]()
Evaluating Compositions of the Form f(g−1(x))
To evaluate compositions of the form ![]() where
where ![]() and
and ![]() are any two of the functions sine, cosine, or tangent and
are any two of the functions sine, cosine, or tangent and ![]() is any input in the domain of
is any input in the domain of ![]() we have exact formulas, such as
we have exact formulas, such as ![]() When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity,
When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity, ![]() to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.
to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.
Evaluating the Composition of a Sine with an Inverse Cosine
Find an exact value for ![]()
Show Solution
Beginning with the inside, we can say there is some angle such that ![]() which means
which means ![]() and we are looking for
and we are looking for ![]() We can use the Pythagorean identity to do this.
We can use the Pythagorean identity to do this.

Since ![]() is in quadrant I,
is in quadrant I, ![]() must be positive, so the solution is
must be positive, so the solution is ![]() See (Figure).
See (Figure).

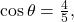 then
then 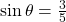
We know that the inverse cosine always gives an angle on the interval ![]() so we know that the sine of that angle must be positive; therefore
so we know that the sine of that angle must be positive; therefore ![]()
Try It
Evaluate ![]()
Show Solution
![]()
Evaluating the Composition of a Sine with an Inverse Tangent
Find an exact value for ![]()
Show Solution
While we could use a similar technique as in (Figure), we will demonstrate a different technique here. From the inside, we know there is an angle such that ![]() We can envision this as the opposite and adjacent sides on a right triangle, as shown in (Figure).
We can envision this as the opposite and adjacent sides on a right triangle, as shown in (Figure).

Using the Pythagorean Theorem, we can find the hypotenuse of this triangle.
Now, we can evaluate the sine of the angle as the opposite side divided by the hypotenuse.
This gives us our desired composition.
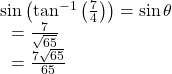
Try It
Evaluate ![]()
Show Solution
![]()
Finding the Cosine of the Inverse Sine of an Algebraic Expression
Find a simplified expression for ![]() for
for ![]()
Show Solution
We know there is an angle ![]() such that
such that ![]()
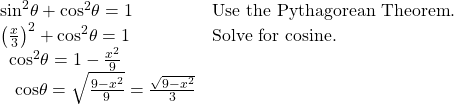
Because we know that the inverse sine must give an angle on the interval ![]() we can deduce that the cosine of that angle must be positive.
we can deduce that the cosine of that angle must be positive.
Try It
Find a simplified expression for ![]() for
for ![]()
Show Solution
![]()
Access this online resource for additional instruction and practice with inverse trigonometric functions.
Visit this website for additional practice questions from Learningpod.
Key Concepts
- An inverse function is one that “undoes” another function. The domain of an inverse function is the range of the original function and the range of an inverse function is the domain of the original function.
- Because the trigonometric functions are not one-to-one on their natural domains, inverse trigonometric functions are defined for restricted domains.
- For any trigonometric function
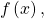 if
if 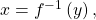 then
then 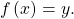 However,
However, 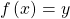 only implies
only implies 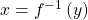 if
if 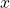 is in the restricted domain of
is in the restricted domain of 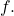 See (Figure).
See (Figure). - Special angles are the outputs of inverse trigonometric functions for special input values; for example,
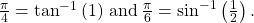 See (Figure).
See (Figure). - A calculator will return an angle within the restricted domain of the original trigonometric function. See (Figure).
- Inverse functions allow us to find an angle when given two sides of a right triangle. See (Figure).
- In function composition, if the inside function is an inverse trigonometric function, then there are exact expressions; for example,
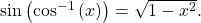 See (Figure).
See (Figure). - If the inside function is a trigonometric function, then the only possible combinations are
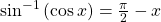 if
if 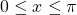 and
and 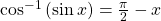 if
if 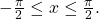 See (Figure) and (Figure).
See (Figure) and (Figure). - When evaluating the composition of a trigonometric function with an inverse trigonometric function, draw a reference triangle to assist in determining the ratio of sides that represents the output of the trigonometric function. See (Figure).
- When evaluating the composition of a trigonometric function with an inverse trigonometric function, you may use trig identities to assist in determining the ratio of sides. See (Figure).
Section Exercises
Verbal
1. Why do the functions ![]() and
and ![]() have different ranges?
have different ranges?
Show Solution
The function ![]() is one-to-one on
is one-to-one on ![]() thus, this interval is the range of the inverse function of
thus, this interval is the range of the inverse function of ![]()
![]() The function
The function ![]() is one-to-one on
is one-to-one on ![]() thus, this interval is the range of the inverse function of
thus, this interval is the range of the inverse function of ![]()
2. Since the functions ![]() and
and ![]() are inverse functions, why is
are inverse functions, why is ![]() not equal to
not equal to ![]()
3. Explain the meaning of ![]()
Show Solution
![]() is the radian measure of an angle between
is the radian measure of an angle between ![]() and
and ![]() whose sine is 0.5.
whose sine is 0.5.
4. Most calculators do not have a key to evaluate ![]() Explain how this can be done using the cosine function or the inverse cosine function.
Explain how this can be done using the cosine function or the inverse cosine function.
5. Why must the domain of the sine function, ![]() be restricted to
be restricted to ![]() for the inverse sine function to exist?
for the inverse sine function to exist?
Show Solution
In order for any function to have an inverse, the function must be one-to-one and must pass the horizontal line test. The regular sine function is not one-to-one unless its domain is restricted in some way. Mathematicians have agreed to restrict the sine function to the interval ![]() so that it is one-to-one and possesses an inverse.
so that it is one-to-one and possesses an inverse.
6. Discuss why this statement is incorrect: ![]() for all
for all ![]()
7. Determine whether the following statement is true or false and explain your answer: ![]()
Show Solution
True . The angle, ![]() that equals
that equals ![]() ,
, ![]() , will be a second quadrant angle with reference angle,
, will be a second quadrant angle with reference angle, ![]() , where
, where ![]() equals
equals ![]() ,
, ![]() . Since
. Since ![]() is the reference angle for
is the reference angle for ![]() ,
, ![]() and
and ![]() =
= ![]() –
–
Algebraic
For the following exercises, evaluate the expressions.
8. ![]()
9. ![]()
Show Solution
![]()
10. ![]()
11. ![]()
Show Solution
![]()
12. ![]()
13. ![]()
Show Solution
![]()
14. ![]()
Show Solution
![]()
16. ![]()
For the following exercises, use a calculator to evaluate each expression. Express answers to the nearest hundredth.
17. ![]()
Show Solution
1.98
18. ![]()
19. ![]()
Show Solution
0.93
20. ![]()
21. ![]()
Show Solution
1.41
For the following exercises, find the angle ![]() in the given right triangle. Round answers to the nearest hundredth.
in the given right triangle. Round answers to the nearest hundredth.
22. 

Show Solution
0.56 radians
For the following exercises, find the exact value, if possible, without a calculator. If it is not possible, explain why.
24. ![]()
25. ![]()
Show Solution
0
26. ![]()
27. ![]()
Show Solution
0.71
28. ![]()
29. ![]()
Show Solution
-0.71
30. ![]()
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
0.8
34. ![]()
35. ![]()
Show Solution
![]()
36. ![]()
For the following exercises, find the exact value of the expression in terms of ![]()
with the help of a reference triangle.
37. ![]()
Show Solution
![]()
38. ![]()
39. ![]()
Show Solution
![]()
40. ![]()
41. ![]()
Show Solution
![]()
Extensions
For the following exercises, evaluate the expression without using a calculator. Give the exact value.
42. ![]()
For the following exercises, find the function if ![]()
43. ![]()
Show Solution
![]()
44. ![]()
45. ![]()
Show Solution
![]()
46. ![]()
47. ![]()
Show Solution
![]()
Graphical
48. Graph ![]() and state the domain and range of the function.
and state the domain and range of the function.
49. Graph ![]() and state the domain and range of the function.
and state the domain and range of the function.
Show Solution

domain ![]() range
range ![]()
50. Graph one cycle of ![]() and state the domain and range of the function.
and state the domain and range of the function.
51. For what value of ![]() does
does ![]() Use a graphing calculator to approximate the answer.
Use a graphing calculator to approximate the answer.
Show Solution
approximately ![]()
52. For what value of ![]() does
does ![]() Use a graphing calculator to approximate the answer.
Use a graphing calculator to approximate the answer.
Real-World Applications
53. Suppose a 13-foot ladder is leaning against a building, reaching to the bottom of a second-floor window 12 feet above the ground. What angle, in radians, does the ladder make with the building?
Show Solution
0.395 radians
54. Suppose you drive 0.6 miles on a road so that the vertical distance changes from 0 to 150 feet. What is the angle of elevation of the road?
55. An isosceles triangle has two congruent sides of length 9 inches. The remaining side has a length of 8 inches. Find the angle that a side of 9 inches makes with the 8-inch side.
Show Solution
1.11 radians
56. Without using a calculator, approximate the value of ![]() Explain why your answer is reasonable.
Explain why your answer is reasonable.
57. A truss for the roof of a house is constructed from two identical right triangles. Each has a base of 12 feet and height of 4 feet. Find the measure of the acute angle adjacent to the 4-foot side.
Show Solution
1.25 radians
58. The line ![]() passes through the origin in the x,y-plane. What is the measure of the angle that the line makes with the positive x-axis?
passes through the origin in the x,y-plane. What is the measure of the angle that the line makes with the positive x-axis?
59. The line ![]() passes through the origin in the x,y-plane. What is the measure of the angle that the line makes with the negative x-axis?
passes through the origin in the x,y-plane. What is the measure of the angle that the line makes with the negative x-axis?
Show Solution
0.405 radians
60. What percentage grade should a road have if the angle of elevation of the road is 4 degrees? (The percentage grade is defined as the change in the altitude of the road over a 100-foot horizontal distance. For example a 5% grade means that the road rises 5 feet for every 100 feet of horizontal distance.)
61. A 20-foot ladder leans up against the side of a building so that the foot of the ladder is 10 feet from the base of the building. If specifications call for the ladder’s angle of elevation to be between 35 and 45 degrees, does the placement of this ladder satisfy safety specifications?
Show Solution
No. The angle the ladder makes with the horizontal is 60 degrees.
62. Suppose a 15-foot ladder leans against the side of a house so that the angle of elevation of the ladder is 42 degrees. How far is the foot of the ladder from the side of the house?
Chapter Review Exercises
Graphs of the Sine and Cosine Functions
For the following exercises, graph the functions for two periods and determine the amplitude or stretching factor, period, midline equation, and asymptotes.
1. ![]()
Show Solution
amplitude: 3; period: ![]() midline:
midline: ![]() no asymptotes
no asymptotes
![A graph of two periods of a function with a cosine parent function. The graph has a range of [0,6] graphed over -2pi to 2pi. Maximums as -pi and pi.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/3252/2018/07/19144218/CNX_Precalc_Figure_06_03_206.jpg)
2. ![]()
3. ![]()
Show Solution
amplitude: 3; period: ![]() midline:
midline: ![]() no asymptotes
no asymptotes
![A graph of four periods of a function with a cosine parent function. Graphed from -4pi to 4pi. Range is [-3,3].](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/3252/2018/07/19144228/CNX_Precalc_Figure_06_03_208.jpg)
4. ![]()
5. ![]()
Show Solution
amplitude: 3; period: ![]() midline:
midline: ![]() no asymptotes
no asymptotes
![A graph of two periods of a sinusoidal function. Range is [-7,-1]. Maximums at -5pi/4 and 3pi/4.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/3252/2018/07/19144234/CNX_Precalc_Figure_06_03_210.jpg)
6. ![]()
7. ![]()
Show Solution
amplitude: 6; period: ![]() midline:
midline: ![]() no asymptotes
no asymptotes
![A sinusoidal graph over two periods. Range is [-7,5], amplitude is 6, and period is 2pi/3.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/3252/2018/07/19144236/CNX_Precalc_Figure_06_03_212.jpg)
8. ![]()
Graphs of the Other Trigonometric Functions
For the following exercises, graph the functions for two periods and determine the amplitude or stretching factor, period,
midline equation, and asymptotes.
9. ![]()
Show Solution
stretching factor: none; period: ![]() midline:
midline: ![]() asymptotes:
asymptotes: ![]() where
where ![]() is an integer
is an integer

10. ![]()
11. ![]()
Show Solution
stretching factor: 3; period: ![]() midline:
midline: ![]() asymptotes:
asymptotes: ![]() where
where ![]() is an integer
is an integer

12. ![]()
For the following exercises, graph two full periods. Identify the period, the phase shift, the amplitude, and asymptotes.
13. ![]()
Show Solution
amplitude: none; period: ![]() no phase shift; asymptotes:
no phase shift; asymptotes: ![]() where
where ![]() is an odd integer
is an odd integer

14. ![]()
15. ![]()
Show Solution
amplitude: none; period: ![]() no phase shift; asymptotes:
no phase shift; asymptotes: ![]() where
where ![]() is an integer
is an integer

16. ![]()
17. ![]()
Show Solution
amplitude: none; period: ![]() no phase shift; asymptotes:
no phase shift; asymptotes: ![]() where
where ![]() is an integer
is an integer

18. ![]()
For the following exercises, use this scenario: The population of a city has risen and fallen over a 20-year interval. Its population may be modeled by the following function:
19. ![]() where the domain is the years since 1980 and the range is the population of the city.
where the domain is the years since 1980 and the range is the population of the city.
What is the largest and smallest population the city may have?
Show Solution
largest: 20,000; smallest: 4,000
20. Graph the function on the domain of ![]() .
.
21. What are the amplitude, period, and phase shift for the function?
Show Solution
amplitude: 8,000; period: 10; phase shift: 0
22. Over this domain, when does the population reach 18,000? 13,000?
23. What is the predicted population in 2007? 2010?
Show Solution
In 2007, the predicted population is 4,413. In 2010, the population will be 11,924.
For the following exercises, suppose a weight is attached to a spring and bobs up and down, exhibiting symmetry.
24. Suppose the graph of the displacement function is shown in (Figure), where the values on the x-axis represent the time in seconds and the y-axis represents the displacement in inches. Give the equation that models the vertical displacement of the weight on the spring.
![A graph of a consine function over one period. Graphed on the domain of [0,10]. Range is [-5,5].](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/3252/2018/07/19144302/CNX_Precalc_Figure_06_03_225.jpg)
25. At time = 0, what is the displacement of the weight?
Show Solution
5 in.
26. At what time does the displacement from the equilibrium point equal zero?
27. What is the time required for the weight to return to its initial height of 5 inches? In other words, what is the period for the displacement function?
Show Solution
10 seconds
Inverse Trigonometric Functions
For the following exercises, find the exact value without the aid of a calculator.
28. ![]()
29. ![]()
Show Solution
![]()
30. ![]()
31. ![]()
Show Solution
![]()
32. ![]()
33. ![]()
Show Solution
![]()
34. ![]()
35. ![]()
Show Solution
No solution
36. ![]()
37. ![]()
Show Solution
![]()
38. ![]()
39. Graph ![]() and
and ![]() on the interval
on the interval ![]() and explain any observations.
and explain any observations.
Show Solution
The graphs are not symmetrical with respect to the line ![]() They are symmetrical with respect to the
They are symmetrical with respect to the ![]() -axis.
-axis.

40. Graph ![]() and
and ![]() and explain any observations.
and explain any observations.
41. Graph the function ![]() on the interval
on the interval ![]() and compare the graph to the graph of
and compare the graph to the graph of ![]() on the same interval. Describe any observations.
on the same interval. Describe any observations.
Show Solution
The graphs appear to be identical.
![Two graphs of two identical functions on the interval [-1 to 1]. Both graphs appear sinusoidal.](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/3252/2018/07/19144312/CNX_Precalc_Figure_06_03_228.jpg)
Glossary
- arccosine
- another name for the inverse cosine;
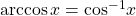
- arcsine
- another name for the inverse sine;
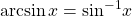
- arctangent
- another name for the inverse tangent;
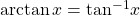
- inverse cosine function
- the function
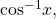 which is the inverse of the cosine function and the angle that has a cosine equal to a given number
which is the inverse of the cosine function and the angle that has a cosine equal to a given number
- inverse sine function
- the function
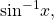 which is the inverse of the sine function and the angle that has a sine equal to a given number
which is the inverse of the sine function and the angle that has a sine equal to a given number
- inverse tangent function
- the function
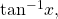 which is the inverse of the tangent function and the angle that has a tangent equal to a given number
which is the inverse of the tangent function and the angle that has a tangent equal to a given number

