Chapter 6.2: Multiplication and Division of Rational Expressions
Multiplying and dividing rational expressions is very similar to the process used to multiply and divide fractions.
Example 1
Reduce and multiply ![]() and
and ![]() .
.
![]()
(15 and 45 reduce to 1 and 3, and 14 and 49 reduce to 2 and 7)
This process of multiplication is identical to division, except the first step is to reciprocate any fraction that is being divided.
Example 2
Reduce and divide ![]() by
by ![]() .
.
![]()
(25 and 15 reduce to 5 and 3, and 6 and 18 reduce to 1 and 3)
When multiplying with rational expressions, follow the same process: first, divide out common factors, then multiply straight across.
Example 3
Reduce and multiply ![]() and
and ![]() .
.
![]()
(25 and 55 reduce to 5 and 11, 24 and 9 reduce to 8 and 3, x2 and x7 reduce to x5, y4 and y8 reduce to y4)
Remember: when dividing fractions, reciprocate the dividing fraction.
Example 4
Reduce and divide ![]() by
by ![]() .
.
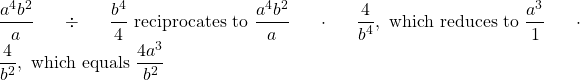
(After reciprocating, 4a4b2 and b4 reduce to 4a3 and b2)
In dividing or multiplying some fractions, the polynomials in the fractions must be factored first.
Example 5
Reduce, factor and multiply ![]() and
and ![]() .
.
![]()
Dividing or cancelling out the common factors ![]() and
and ![]() leaves us with
leaves us with ![]() , which results in
, which results in ![]() .
.
Example 6
Reduce, factor and multiply or divide the following fractions:
![]()
Factoring each fraction and reciprocating the last one yields:
![]()
Dividing or cancelling out the common polynomials leaves us with:
![]()
Questions
Simplify each expression.
Answers to odd questions
1. ![]()
3. ![]()
5. ![]()
7. 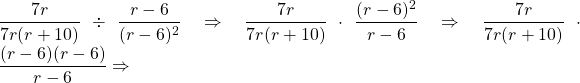
![]()
9. ![]()
11. ![]()
13. ![]()
15. ![]()
![]()
17. ![]()
19. ![]()
21. ![]()
![]()
23. ![]()
![]()

