Chapter 5.5: Factoring Special Products

Now transition from multiplying special products to factoring special products. If you can recognize them, you can save a lot of time. The following is a list of these special products (note that a²+ b² cannot be factored):

$\begin{array}{lll} a^2-b^2&=&(a+b)(a-b) \\ (a+b)^2&=&a^2+2ab+b^2 \\ (a-b)^2&=&a^2-2ab+b^2 \\ a^3-b^3&=&(a-b)(a^2+ab+b^2) \\ a^3+b^3&=&(a+b)(a^2-ab+b^2) \\ \end{array}$

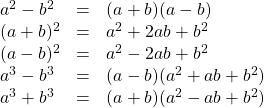
The challenge is therefore in recognizing the special product.

Example 1

Factor $x^2 - 36$ .

This is a difference of squares. $(x - 6)(x + 6)$ is the solution.

Example 2

Factor $x^2 - 6x + 9$ .

This is a perfect square. $(x - 3)(x - 3)$ or $(x - 3)^2$ is the solution.

Example 3

Factor $x^2 + 6x + 9$ .

This is a perfect square. $(x + 3)(x + 3)$ or $(x + 3)^2$ is the solution.

Example 4

Factor $4x^2 + 20xy + 25y^2$ .

This is a perfect square. $(2x + 5y)(2x + 5y)$ or $(2x + 5y)^2$ is the solution.

Example 5

Factor $m^3 - 27$ .

This is a difference of cubes. $(m - 3)(m^2 + 3m + 9)$ is the solution.

Example 6

Factor $125p^3 + 8r^3$ .

This is a difference of cubes. $(5p + 2r)(25p^2 - 10pr + 4r^2)$ is the solution.

Questions

Factor each of the following polynomials.

$r^2-16$
$x^2-9$
$v^2-25$
$x^2-1$
$p^2-4$
$4v^2-1$
$3x^2-27$
$5n^2-20$
$16x^2-36$
$125x^2+45y^2$
$a^2-2a+1$
$k^2+4k+4$
$x^2+6x+9$
$n^2-8n+16$
$25p^2-10p+1$
$x^2+2x+1$
$25a^2+30ab+9b^2$
$x^2+8xy+16y^2$
$8x^2-24xy+18y^2$
$20x^2+20xy+5y^2$
$8-m^3$
$x^3+64$
$x^3-64$
$x^3+8$
$216-u^3$
$125x^3-216$
$125a^3-64$
$64x^3-27$
$64x^3+27y^3$
$32m^3-108n^3$

Answers to odd questions

1. $(r-4)(r+4)$

3. $(v-5)(v+5)$

5. $(p-2)(p+2)$

7. $3(x^2-9)$
$3(x-3)(x+3)$

9. $4(4x^2-9)$
$4(2x-3)(2x+3)$

11. $(a-1)^2$

13. $(x+3)^2$

15. $(5p-1)^2$

17. $(5a+3b)^2$

19. $2(4x^2-12xy+9y^2)$
$2(2x-3y)^2$

21. $(2-m)(4+2m+m^2)$

23. $(x-4)(x^2+4x+16)$

25. $(6-u)(36+6u+u^2)$

27. $(5a-4)(25a^2+20a+16)$

29. $(4x+3y)(16x^2-12xy+9y^2)$

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Pre-Calculus Copyright © 2022 by St. Clair College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book