Chapter 5.1: Greatest Common Factor
The opposite of multiplying polynomials together is factoring polynomials. Factored polynomials help to solve equations, learn behaviours of graphs, work with fractions and more. Because so many concepts in algebra depend on us being able to factor polynomials, it is important to have very strong factoring skills.
In this section, the focus is on factoring using the greatest common factor or GCF of a polynomial. When you previously multiplied polynomials, you multiplied monomials by polynomials by distributing, solving problems such as ![]() to yield
to yield ![]() . For factoring, you will work the same problem backwards. For instance, you could start with the polynomial
. For factoring, you will work the same problem backwards. For instance, you could start with the polynomial ![]() and work backwards to
and work backwards to ![]() .
.
To do this, first identify the GCF of a polynomial. Look at finding the GCF of several numbers. To find the GCF of several numbers, look for the largest number that each of the numbers can be divided by.
Example 1
Find the GCF of 15, 24, 27.
First, break all these numbers into their primes.
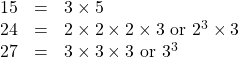
By observation, the only number that each can be divided by is 3. Therefore, the GCF = 3.
Example 2
Find the GCF of ![]() ,
, ![]() , and
, and ![]() .
.
First, break all these numbers into their primes. (Use • to designate multiplication instead of ×.)
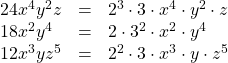
By observation, what is shared between all three monomials is ![]() or
or ![]() .
.
Questions
Factor out the common factor in each of the following polynomials.
Answers to odd questions
1. ![]()
3. ![]()
5. ![]()
7. ![]()
9. ![]()
11. ![]()
13. ![]()
15. ![]()
17. ![]()
19. ![]()
21. ![]()
23. ![]()
25. ![]()

