Chapter 8: Solutions to Exercises

8.1 Principal, Rate, Time

1. If you want to earn $1,000 of simple interest at a rate of 7% in a span of five months, how much money must you invest?

Solution:

Step 1: Given information:

$I=\mathrm{\$}1,000$; $r=7\mathrm{\%}\text{annually}$; $t=5\text{months}$

Step 2: Convert monthly $t$ to match annual $r$; $t=\frac{5}{12}$

Step 3: Solve for $P$.

$\begin{array}{}\text{(1)}& P& =\frac{I}{rt}\text{(2)}& & =\frac{\mathrm{\$}1,000}{0.07\left(\frac{5}{12}\right)}\text{(3)}& & =\mathrm{\$}34,285.71\end{array}$

I must invest $34,285.71.

2. If you placed $2,000 into an investment account earning 3% simple interest, how many months does it take for you to have $2,025 in your account?

Solution:

Step 1: Given information:

$I=\mathrm{\$}2,025-\mathrm{\$}2,000=\mathrm{\$}25$; $P=\mathrm{\$}2,000$; $r=3\mathrm{\%}\text{annually}$

Step 2: Convert annual $r$ to match monthly $t$; $r=\frac{3\mathrm{\%}}{12}$

Step 3: Solve for $t$.

$\begin{array}{}\text{(4)}& t& =\frac{I}{Pr}\text{(5)}& & =\frac{\mathrm{\$}25}{\mathrm{\$}2,000\left(\frac{0.03}{12}\right)}\text{(6)}& & =5\text{months}\end{array}$

It takes 5 months to have $2,025 in the account.

3. A $3,500 investment earned $70 of interest over the course of six months. What annual rate of simple interest did the investment earn?

Solution:

Step 1: Given information:

$P=\mathrm{\$}3,500$; $I=\mathrm{\$}70$; $t=6\text{months}$

Step 2: Convert the time period from months to years; $t=\frac{6}{12}$

Step 3: Solve for $r$.

$\begin{array}{}\text{(7)}& r& =\frac{I}{Pt}\text{(8)}& & =\frac{\mathrm{\$}70}{\mathrm{\$}3,500\left(\frac{6}{12}\right)}\text{(9)}& & =0.04\text{or}4\mathrm{\%}\end{array}$

The investment earned 4% simple interest.

Time and Dates

1. Brynn borrowed $25,000 at 1% per month from a family friend to start her entrepreneurial venture on December 2, 2011. If she paid back the loan on June 16, 2012, how much simple interest did she pay? 

Solution:

Step 1: Given information:

$P=\mathrm{\$}25,000$; $r=1\mathrm{\%}\text{monthly}$; $t=\text{December}2,2011\text{to June}16,2012$

Use DATE function on calculator to get the number of days. Total days for $t=197$

Step 2: Convert both the monthly $r$ and the daily $t$ to annual numbers;

$r=1\mathrm{\%}\times 12=12\mathrm{\%}\text{annually};$ $t=\frac{197}{365}$

Step 3: Solve for $I$.

$\begin{array}{}\text{(10)}& I& =Prt\text{(11)}& & =\mathrm{\$}25,000(0.12)\left(\frac{197}{365}\right)\text{(12)}& & =\mathrm{\$}1,619.18\end{array}$

She payed $1,619.18 simple interest. 

2. If $6,000 principal plus $132.90 of simple interest was withdrawn on August 14, 2011, from an investment earning 5.5% interest, on what day was the money invested? 

Solution:

Need to calculate $t$ in days first.

Step 1: Given information:

$I=\mathrm{\$}132.90$; $P=\mathrm{\$}6,000$; $r=5.5\mathrm{\%}\text{annually}$

Step 2: Convert annual $r$ to match daily $t$; $r=\frac{5.5\mathrm{\%}}{365}$

Step 3: Solve for $t$.

$\begin{array}{}\text{(13)}& t& =\frac{I}{Pr}\text{(14)}& & =\frac{\mathrm{\$}132.90}{\mathrm{\$}6,000\left(\frac{0.055}{365}\right)}\text{(15)}& & =146.995454\text{days}\to 147\text{days}\end{array}$

Use the DATE function on the calculator to find the date when the money was invested.

The money was invested on March 20, 2011.

8.2 Moving Money Involving Simple Interest

1. An accountant needs to allocate the principal and simple interest on a loan payment into the appropriate ledgers. If the amount received was $10,267.21 for a loan that spanned April 14 to July 31 at 9.1%, how much was the principal and how much was the interest?

Solution:

Step 1: Given information:

$S=\mathrm{\$}10,267.21$; $r=9.1\mathrm{\%}\text{annually}$; $t=\text{April}14\text{to July}31=108\text{days}$

Step 2: Convert daily $t$ to match annual $r$; $t=\frac{108}{365}$

Step 3: Solve for $P$.

$\begin{array}{}\text{(16)}& P& =\frac{S}{1+rt}\text{(17)}& & =\frac{\mathrm{\$}10,267.21}{1+0.091\times \frac{108}{365}}\text{(18)}& & =\mathrm{\$}9,998\end{array}$

Step 4: Solve for $I$.

$\begin{array}{}\text{(19)}& I& =S-P\text{(20)}& & =\mathrm{\$}10,267.21-\mathrm{\$}9,998\text{(21)}& & =\mathrm{\$}269.21\end{array}$

The principal was $9,998 and the simple interest on the loan was $269.21.

2. Suppose Robin borrowed $3,600 on October 21 and repaid the loan on February 21 of the following year. What simple interest rate was charged if Robin repaid $3,694.63? 

Solution:

Step 1: Given information:

$P=\mathrm{\$}3,600$; $S=\mathrm{\$}3,694.63$; $t=\text{October}21\text{to February}21=123\text{days}$

Step 2: Compute $I$.

$\begin{array}{}\text{(22)}& I& =S-P\text{(23)}& & =\mathrm{\$}3,694.63-\mathrm{\$}3,600\text{(24)}& & =\mathrm{\$}94.63\end{array}$

Step 3: Convert daily $t$ to match annual $r$; $t=\frac{123}{365}$

Step 4: Solve for $r$.

$\begin{array}{}\text{(25)}& r& =\frac{I}{Pt}\text{(26)}& & =\frac{\mathrm{\$}94.63}{\mathrm{\$}3,600\left(\frac{123}{365}\right)}\text{(27)}& & =0.078004\text{or}7.8004\mathrm{\%}\end{array}$

The simple interest charged was 7.80%.

3. Jayne needs to make three payments to Jade requiring $2,000 each 5 months, 10 months, and 15 months from to day. She proposes instead making a single payment eight months from today. If Jade agrees to a simple interest rate of 9.5%, what amount should Jayne pay? 

Solution:

Step 1: Given information:

$r=9.5\mathrm{\%}\text{annually}$

Payment #1: $P=\mathrm{\$}2,000$; $t=8\text{months}-5\text{months}=3\text{months}$
Payment #2: $S=\mathrm{\$}2,000$; $t=10\text{months}-8\text{months}=2\text{months}$
Payment #3: $S=\mathrm{\$}2,000$; $t=15\text{months}-8\text{months}=7\text{months}$

Replacement payment is eight months from today.

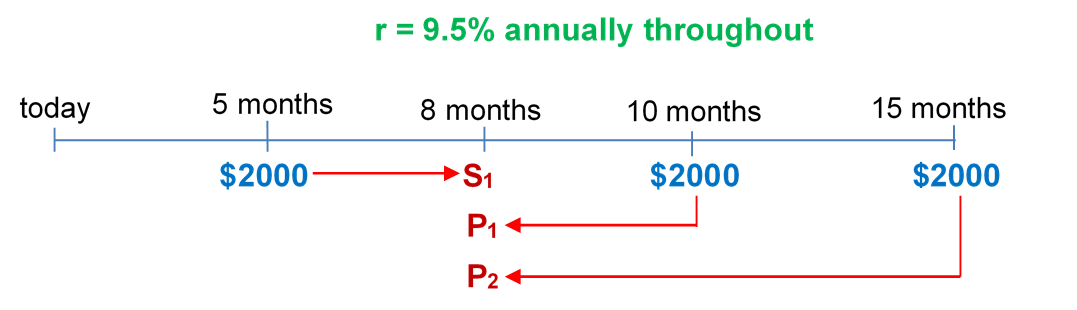
Payment #1:

Step 2: Convert monthly $t$ to match annual $r$; $t=\frac{3}{12}$

Step 3: Solve for $S_1$.

$\begin{array}{}\text{(28)}& S_1& =P(1+rt)\text{(29)}& & =\mathrm{\$}2,000\times (1+0.095\times \frac{3}{12})\text{(30)}& & =\mathrm{\$}2,000\times 1.02375\text{(31)}& & =\mathrm{\$}2,047.50\end{array}$

Payment #2:

Step 2: Convert monthly $t$ to match annual $r$; $t=\frac{2}{12}$

Step 3: Solve for $P_1$.

$\begin{array}{}\text{(32)}& P_1& =\frac{S}{1+rt}\text{(33)}& & =\frac{\mathrm{\$}2,000}{1+0.095\times \frac{2}{12}}\text{(34)}& & =\frac{\mathrm{\$}2,000}{1.0158\bar{3}}\text{(35)}& & =\mathrm{\$}1,968.83\end{array}$

Payment #3:

Step 2: Convert monthly $t$ to match annual $r$; $t=\frac{7}{12}$

Step 3: Solve for $P_2$.

$\begin{array}{}\text{(36)}& P_2& =\frac{S}{1+rt}\text{(37)}& & =\frac{\mathrm{\$}2,000}{1+0.095\times \frac{7}{12}}\text{(38)}& & =\frac{\mathrm{\$}2,000}{1.05541\bar{6}}\text{(39)}& & =\mathrm{\$}1,894.99\end{array}$

$\begin{array}{}\text{(40)}& \text{Replacement payment eight months from today}& =\mathrm{\$}2,047.50+\mathrm{\$}1,968.83+\mathrm{\$}1,894.99\text{(41)}& & =\$5,911.32\end{array}$

Jayne should pay $5,911.32.

4. Merina is scheduled to make two loan payments to Bradford in the amount of $1,000 each, two months and nine months from now. Merina doesn’t think she can make those payments and offers Bradford an alternative plan where she will pay $775 seven months from now and another payment seven months later. Bradford determines that 8.5% is a fair interest rate. What is the amount of the second payment? 

Solution:

The unknown payment is 14 months from today.

On the original loan payments, both payments are late and should be charged interest.

Under the proposed payments, need to calculate the equivalent payment for the seven month payment on the 14 month day so that the amount remaining for the second payment can be determined.  These payments should be equivalent to the original loan payments.

Step 1: Given information:

$r=8.5\mathrm{\%}\text{annually}$

Original Agreement:

Payment #1: $P=\mathrm{\$}1,000$; $t=14\text{months}-2\text{months}=12\text{months late}$
Payment #2: $P=\mathrm{\$}1,000$; $t=14\text{months}-9\text{months}=5\text{months late}$

Proposed Agreement:

Payment #1: $P=\mathrm{\$}775$; $t=14\text{months}-7\text{months}=7\text{months}$
Payment #2: Unknown (x), but 14 months from today.

Original Agreement Payment #1:

Step 2: Convert monthly $t$ to match annual $r$ ; $t=\frac{12}{12}=1\text{year}$

Step 3: Solve for $S_1$.

$\begin{array}{}\text{(42)}& S_1& =P(1+rt)\text{(43)}& & =\mathrm{\$}1,000\times (1+0.085\times 1)\text{(44)}& & =\mathrm{\$}1,085\end{array}$

Original Agreement Payment #2:

Step 2: Convert monthly $t$ to match annual $r$; $t=\frac{5}{12}$

Step 3: Solve for $S_2$.

$\begin{array}{}\text{(45)}& S_2& =P(1+rt)\text{(46)}& & =\mathrm{\$}1,000\times (1+0.085\times \frac{5}{12})\text{(47)}& & =\mathrm{\$}1,035.42\end{array}$

Proposed Agreement Payment #1:

Step 2: Convert monthly $t$ to match annual $r$ ; $t=\frac{7}{12}$

Step 3: Solve for $S_3$.

$\begin{array}{}\text{(48)}& S_3& =P(1+rt)\text{(49)}& & =\mathrm{\$}775\times (1+0.085\times \frac{7}{12})\text{(50)}& & =\mathrm{\$}813.43\end{array}$

Now make the two agreements equivalent to each other.

$\begin{array}{}\text{(51)}& \text{Total owing under original agreement}& =\text{Total owing under proposed agreement}\text{(52)}& \mathrm{\$}1,085+\mathrm{\$}1,035.42& =\mathrm{\$}813.43+x\text{(53)}& x& =\mathrm{\$}1,306.99\end{array}$

To make the alternate loan payments equivalent to the original payments, Merina must pay $1,306.99  14 months from today.

8.3 Savings Accounts and Short-Term GICs

1. Canadian Western Bank offers a Summit Savings Account with posted interest rates as indicated in the table below. Only each tier is subject to the posted rate, and interest is calculated daily based on the closing balance.

December’s opening balance was $550,000. Two deposits in the amount of $600,000 each were made on December 3 and December 21. Two withdrawals in the amount of $400,000 and $300,000 were made on December 13 and December 24, respectively. What interest for the month of December will be deposited to the account on January 1?

Solution:

Step 1: Interest rates as per table in question.

December opening balance = $550,000
December 3 Deposit = $600,000
December 13 Withdrawal = $400,000
December 21 Deposit = $600,000
December 24 Withdrawal = $300,000

Step 2: Set up Table.

Step 3: Total Monthly Interest Earned, $I$.

$\begin{array}{}\text{(70)}& I& =\mathrm{\$}31.356164+\mathrm{\$}286.232876+\mathrm{\$}32.876712+\mathrm{\$}171.452054+\mathrm{\$}85.869863+\mathrm{\$}23.013698+\mathrm{\$}228.986301+\mathrm{\$}8.767123\text{(71)}& I& =\$868.55\end{array}$

The total monthly interest earned is $868.55.

2. If you place $25,500 into an 80-day short-term GIC at TD Canada Trust earning 0.55% simple interest, how much will you receive when the investment matures?

Solution:

Step 1: Given information:

$P=\mathrm{\$}25,500$; $t=80\text{days}$; $r=0.55\mathrm{\%};\text{annually}$

Step 2: Convert daily $t$ to match annual $r$; $t=\frac{80}{365}$

Step 3: Solve for $S$.

$\begin{array}{}\text{(72)}& S& =P(1+rt)\text{(73)}& & =\mathrm{\$}25,500\times (1+0.0055\times \frac{80}{365})\text{(74)}& & =\mathrm{\$}25,530.74\end{array}$

When the investment matures I will receive $25,530.74.

3. Interest rates in the GIC markets are always fluctuating be cause of changes in the short-term financial markets. If you have $50,000 to invest today, you could place the money  into a 180-day GIC at Canada Life earning a fixed rate of 0.4%, or you could take two consecutive 90-day GICs. The current posted fixed rate on 90-day GICs at Canada Life is 0.3%. Trends in the short-term financial markets suggest that within the next 90 days short-term GIC rates will be rising. What does the short-term 90-day rate need to be 90 days from now to arrive at the same maturity value as the 180-day GIC? Assume that the entire maturity value of the first 90-day GIC would be reinvested. 

Solution:

Step 1: Given information:

For the first GIC investment option:

$P=\mathrm{\$}50,000$; $r=0.4\mathrm{\%}\text{per year}$; $t=180\text{days}$

For the second GIC investment option:

Initial $P=\mathrm{\$}50,000$; $r=0.3\mathrm{\%}\text{per year}$; $t=90\text{days}$

then,

$P=S\text{of first 90-day GIC}$; $S=\text{maturity value of}180-\text{day GIC}$;
$t=90\text{days}$

Step 2: Transforming both time variables; $t=\frac{180}{365}$ and $t=\frac{90}{365}$

Step 3: (1st GIC option):

$\begin{array}{}\text{(75)}& S_1& =\mathrm{\$}50,000(1+0.004\times \frac{180}{365})\text{(76)}& & =\mathrm{\$}50,098.63\end{array}$

Step 3: (2nd GIC option, 1st GIC):

$\begin{array}{}\text{(77)}& S_2& =\mathrm{\$}50,000(1+0.003\times \frac{90}{365})\text{(78)}& & =\mathrm{\$}50,036.99\end{array}$

Step 3: (2nd GIC option, 2nd GIC):

$I=(\text{S of}180-\text{day GIC})–(\text{S of}90-\text{day GIC})$

$\begin{array}{}\text{(79)}& I& =\mathrm{\$}50,098.63-\mathrm{\$}50,036.99\text{(80)}& & =\mathrm{\$}61.64(\text{what the second 90-day GIC must earn in interest})\end{array}$

$\begin{array}{}\text{(81)}& r& =\frac{I}{Pt}\text{(82)}& & =\frac{\mathrm{\$}61.64}{\mathrm{\$}50,036.99\left(\frac{90}{365}\right)}\text{(83)}& & =0.004995\text{or}0.4995\mathrm{\%}\end{array}$

The short-term 90-day rate needs to be 0.50% 90 days from now to arrive at the same maturity value as the 180-day GIC.

8.6: Application: Treasury Bills & Commercial Papers

1. A 60-day, $90,000 face value commercial paper was issued when yields were 2.09%. What was its purchase price? 

Solution:

Step 1: Given information:

$t=\frac{60}{365}$; $r=2.09\mathrm{\%}$; $S=\mathrm{\$}90,000$

Step 2: Solve for $P$.

$\begin{array}{}\text{(84)}& P& =\frac{S}{1+rt}\text{(85)}& & =\frac{\mathrm{\$}90,000}{1+0.0209\times \frac{60}{365}}\text{(86)}& & =\mathrm{\$}89,691.85\end{array}$

Its purchase price was $89,691.85.

2. A 90-day Province of Ontario T-bill with a $35,000 face value matures on December 11. Farrah works for Hearthplace Industries and notices that the company temporarily has some extra cash available. If she invests the money on October 28, when the yield is 4.94%, and sells the T-bill on November 25, when the yield is 4.83%, calculate how much money Farrah earned and the rate of return she realized. 

Solution:

Calculate the purchase price for the T-bill:

Step 1: Given information:

$r=4.94\mathrm{\%}(\text{only the rate on the day of purchase matters})$; $S=\mathrm{\$}35,000$

$\begin{array}{}\text{(87)}& t& =\text{October}28\text{to December}11\text{(88)}& & =3+30+11\text{(89)}& & =44\text{days left on T-bill or}44/365\end{array}$

(Only the time remaining on the T-bill is important.)

Step 2: Solve for $P$.

$\begin{array}{}\text{(90)}& P& =\frac{S}{1+rt}\text{(91)}& & =\frac{\mathrm{\$}35,000}{1+0.0494\times \frac{44}{365}}\text{(92)}& & =\mathrm{\$}34,792.81\end{array}$

Calculate the price when sold for the T-bill:

Step 1: Given information:

$r=4.83\mathrm{\%}(\text{only the rate on the day of sale matters})$; $S=\mathrm{\$}35,000$

$\begin{array}{}\text{(93)}& t& =\text{November}25\text{to December}11\text{(94)}& & =5+11\text{(95)}& & =16\text{days left on T-bill or}16/365\end{array}$

(Only the time remaining on the T-bill is important.)

Step 2: Solve for $P$.

$\begin{array}{}\text{(96)}& P& =\frac{S}{1+rt}\text{(97)}& & =\frac{\mathrm{\$}35,000}{1+0.0483\times \frac{16}{365}}\text{(98)}& & =\mathrm{\$}34,926.05\end{array}$

Calculate the amount of interest:

$\begin{array}{}\text{(99)}& \text{Amount earned}& =\text{Sold price}-\text{Purchase price}\text{(100)}& & =\mathrm{\$}34,926.05-\mathrm{\$}34,792.81\text{(101)}& & =\mathrm{\$}133.24\end{array}$

Calculate Farrah’s rate of return:

Step 1: Given information:

$I=\mathrm{\$}133.24$; $P=\mathrm{\$}34,792.81$

$\begin{array}{}\text{(102)}& t& =\text{October}28\text{to November}25(\text{the time held})\text{(103)}& & =3+25\text{(104)}& & =28\text{days or}28/365\end{array}$

Step 2: Solve for $r$.

$\begin{array}{}\text{(105)}& r& =\frac{I}{Pt}\text{(106)}& & =\frac{\mathrm{\$}133.24}{\mathrm{\$}34,792.81\times \frac{28}{365}}\text{(107)}& & =0.049920\text{or}4.99\mathrm{\%}\end{array}$

Farrah earned $133.24 and the rate of return she realized was 4.99%.

3. Philippe purchased a $100,000 Citicorp Financial 220-day commercial paper for $96,453.93. He sold it 110 days later to Damien for $98,414.58, who then held onto the commercial paper until its maturity date.
   a) What is Philippe’s actual rate of return?
   b) What is Damien’s actual rate of return?
   c) What is the rate of return Philippe would have realized if he had held onto the note instead of selling it to Damien?

Solution:

a)

Step 1: Given information:

$P=\mathrm{\$}96,453.93$; $t=\frac{110}{365}$; $S=\mathrm{\$}98,414.58$

Step 2: Calculate $I$.

$\begin{array}{}\text{(108)}& I& =S-P\text{(109)}& & =\mathrm{\$}98,414.58-\mathrm{\$}96,453.93\text{(110)}& & =\mathrm{\$}1,960.65\end{array}$

Step 3: Solve for $r$.

$\begin{array}{}\text{(111)}& r& =\frac{I}{Pt}\text{(112)}& & =\frac{\mathrm{\$}1,960.65}{\mathrm{\$}96,453.93\times \frac{110}{365}}\text{(113)}& & =0.067449\text{or}6.74\mathrm{\%}\end{array}$

Philippe’s actual rate of return is 6.74%.

b)

Step 1: Given information:

$S=\mathrm{\$}100,000$; $t=\frac{110}{365}$; $P=\mathrm{\$}98,414.58$

Step 2: Calculate $I$.

$\begin{array}{}\text{(114)}& I& =S-P\text{(115)}& & =\mathrm{\$}100,000-\mathrm{\$}98,414.58\text{(116)}& & =\mathrm{\$}1,585.42\end{array}$

Step 3: Solve for $r$.

$\begin{array}{}\text{(117)}& r& =\frac{I}{Pt}\text{(118)}& & =\frac{\mathrm{\$}1,585.42}{\mathrm{\$}98,414.58\times \frac{110}{365}}\text{(119)}& & =0.053454\text{or}5.35\mathrm{\%}\end{array}$

Damien’s actual rate of return is 5.35%.

c)

Step 1: Given information:

$S=\mathrm{\$}100,000$; $t=\frac{220}{365}$; $P=\mathrm{\$}96,453.93$

Step 2: Solve for $I$.

$\begin{array}{}\text{(120)}& I& =S-P\text{(121)}& & =\mathrm{\$}100,000-\mathrm{\$}96,453.93\text{(122)}& & =\mathrm{\$}3,546.07\end{array}$

Step 3: Solve for $r$.

$\begin{array}{}\text{(123)}& r& =\frac{I}{Pt}\text{(124)}& & =\frac{\mathrm{\$}3,546.07}{\mathrm{\$}96,453.93\times \frac{220}{365}}\text{(125)}& & =0.060995\text{or}6.10\mathrm{\%}\end{array}$

Philippe would have realized 6.10% rate of return if he had held onto the note instead of selling it to Damien.

Image Descriptions

Figure 8.2.2:  Timeline showing $2000 at 5 months from today moving to 8 months from today as S₁. $2000 at 10 months from today moving back to 8 months from today as P₁. $2000 at 15 months from today moving back to 8 months from today as P₂. Interest rate r = 9.5% annually throughout. [Back to Figure 8.2.2]

Figure 8.2.4: Timeline showing the Original Agreement of $1000 at 2 months from today moving to 14 months from today as S₁ and $1000 at 9 months from today moving to 14 months from today as S₂. The Proposed Agreement shows $750 at 7 months from today moving to 14 months from today as S₃ and X at 14 months from today. [Back to Figure 8.2.4]