Chapter 11: Solution to Exercises

11.1: Fundamentals of Annuities

1. Each year, Buhler Industries saves up $1 million to distribute in Christmas bonuses to its employees. To do so, at the end of every month the company invests $81,253.45 into an account earning 5.5% compounded monthly. Calculate the number of the payments (investments).

Solution:

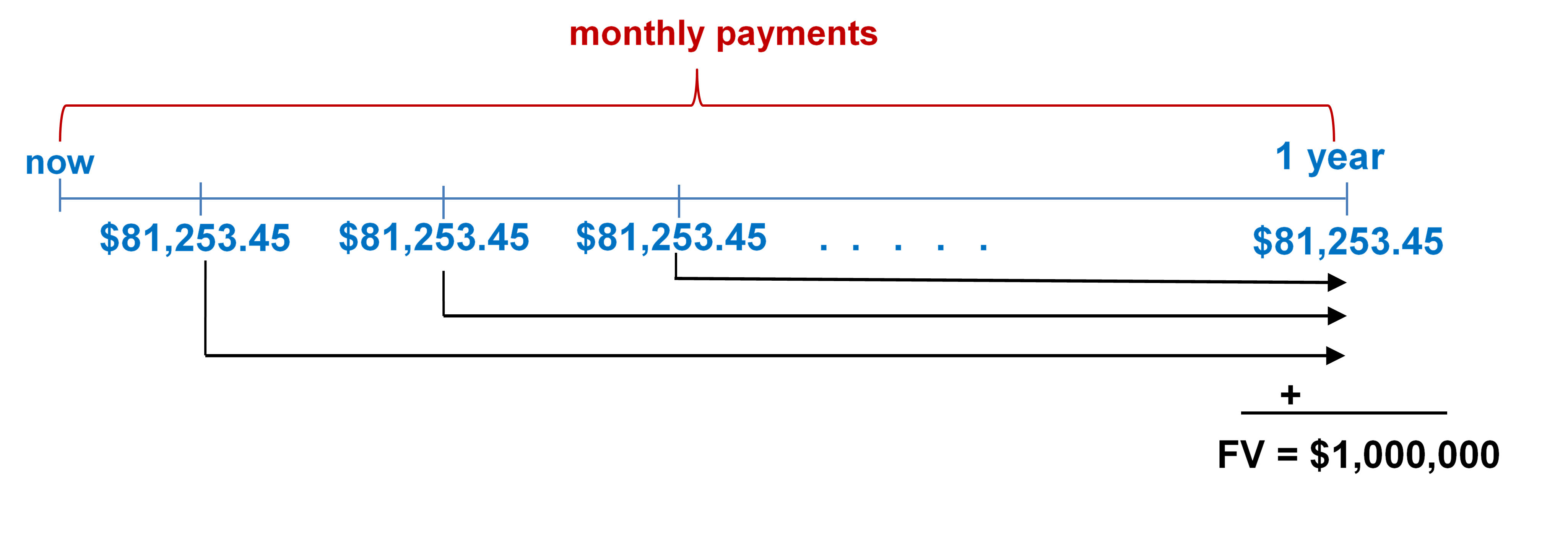
Annuity type is Ordinary Simple Annuity (payment and compounding frequencies coincide and payments at end of the interval).

Step 1: Given information:

[latex]\text{Years} = 1[/latex]; [latex]P/Y = \text{monthly} = 12[/latex]

Step 2: Calculate [latex]N[/latex].

[latex]N= (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 1 \times 12= 12 \;\text{payments}[/latex]

2. Marie has decided to start saving for a down payment on her home. If she puts $1,000 every quarter for five years into a GIC earning 6% compounded monthly she will have $20,979.12. She will make her first deposit three months from now. Draw an annuity timeline and determine the annuity type. Calculate the number of the payments (deposits).

Solution:

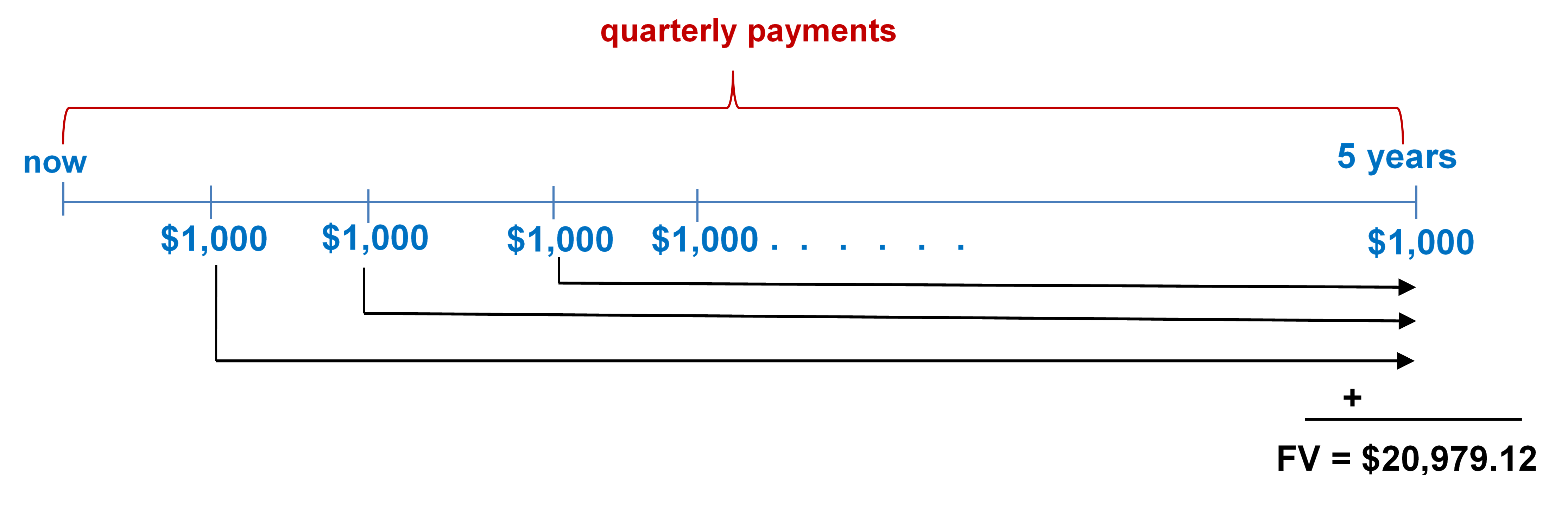
Annuity type is Ordinary General Annuity (payment and compounding frequencies do not coincide and payments at end of the interval).

Step 1: Given information.

[latex]\text{Years} = 5[/latex]; [latex]P/Y = \text{quarterly} = 4[/latex]

Step 2: Calculate [latex]N[/latex].

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 5 \times 4= 20 \;\text{payments}[/latex]

3. Steve takes out a two-year gym membership worth $500. The first of his monthly $22.41 payments is due at signing and includes interest at 8% compounded annually. Calculate the number of the payments.

Solution:

Annuity type is General Annuity Due (payment and compounding frequencies do not coincide and payments at beginning of the interval).

Step 1: Given information.

[latex]\text{Years} = 2[/latex]; [latex]P/Y = \text{monthly} = 12[/latex]

Step 2: Calculate [latex]N[/latex]

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 2 \times 12= 24 \;\text{payments}[/latex]

11.2: Future Value of Annuities

1. You are a financial adviser. Your client is thinking of investing $600 at the end of every six months for the next six years with the invested funds earning 6.4% compounded semi-annually. Your client wants to know how much money she will have after six years. What do you tell your client?

Solution:

Using BA2+ calculator:

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 6 \times 2 = 12 \;\text{payments}[/latex]
[latex]I/Y = 6.4[/latex]
[latex]P/Y = 2[/latex]
[latex]PV = 0[/latex]
[latex]C/Y = 2[/latex]
[latex]PMT = -600[/latex]
[latex]CPT\; FV = \$8,\!612.62[/latex]

The client will have $8,612.62 after six years.

2. McDonald’s major distribution partner, The Martin-Brower Company, needs at least $1 million to build a new warehouse in Medicine Hat two years from today. To date, it has invested $500,000. If it continues to invest $50,000 at the end of every quarter into a fund earning 6% quarterly, will it have enough money to build the warehouse two years from now? Show calculations to support your answer.

Solution:

Using BA2+ calculator:

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 2 \times 4 = 8\;\text{payments}[/latex]
[latex]I/Y = 6[/latex]
[latex]P/Y = 4[/latex]
[latex]C/Y = 4[/latex]
[latex]PV = -500,\!000[/latex]
[latex]PMT = -50,\!000[/latex]
[latex]CPT \;FV = \$984,\!1888.25[/latex]

No, the fund is $15,111.75 ($1,000,000 ‒ $984,888.25) short of the money required.

3. The Saskatchewan Roughriders started a rainy-day savings fund three-and-a-half years ago to help pay for stadium improvements. At the beginning of every quarter the team has deposited $20,000 into the fund, which has been earning 4.85% compounded semi-annually. How much money is in the fund today?

Solution:

Using BA2+ calculator:

Mode = BGN

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 3.5 \times 4 = 14\;\text{payments}[/latex]
[latex]I/Y = 4.85[/latex]
[latex]P/Y = 4[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 0[/latex]
[latex]PMT = -20,\!000[/latex]
[latex]CPT \;FV_\text{due} = \$306,\!680.93[/latex]

$306,680.93 is in the fund today.

4. Carlyle plans to make month-end contributions of $400 to his RRSP from age 20 to age 40. From age 40 to age 65, he plans to make no further contributions to his RRSP. The RRSP can earn 9% compounded annually from age 20 to age 60, and then 5% compounded annually from age 60 to age 65. Under this plan, what is the maturity value of his RRSP when he turns 65?

Solution:

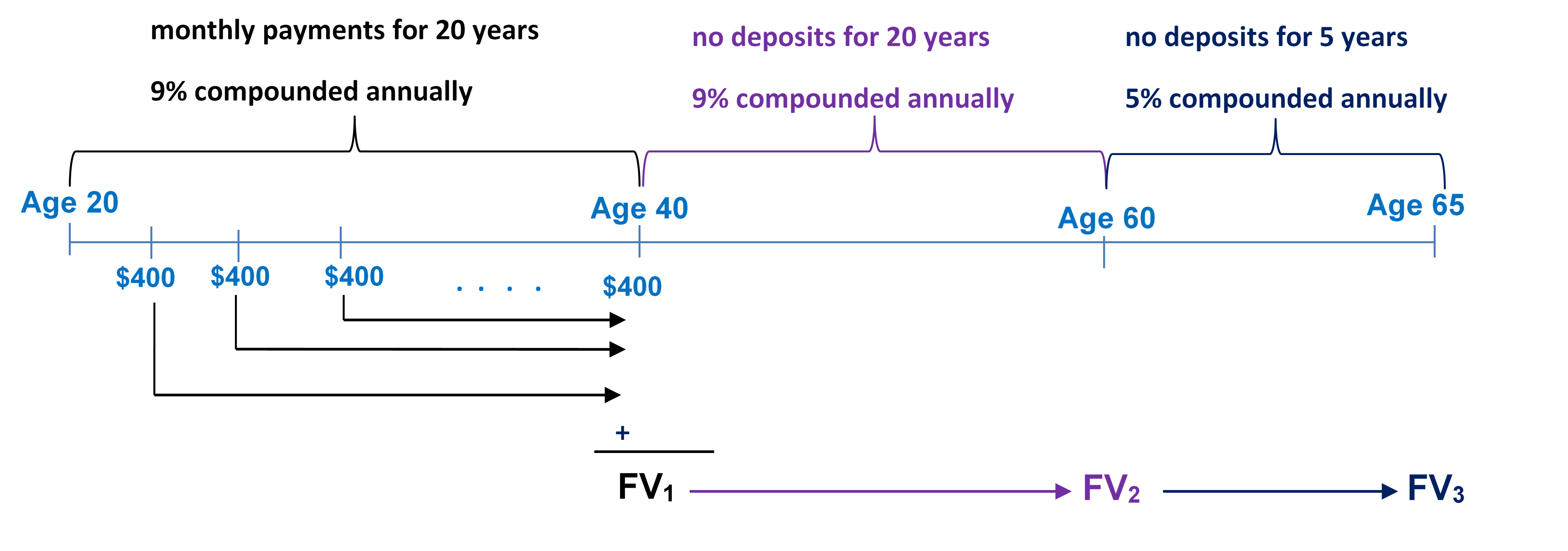
Using BA2+ calculator:

Mode = END

Step 1: Find [latex]FV_1[/latex].

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 20 \times 12 = 240\;\text{payments}[/latex]
[latex]I/Y = 9[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 1[/latex]
[latex]PV = 0[/latex]
[latex]PMT = -400[/latex]
[latex]CPT \;FV_\text{1} = \$255,540.6808\; \text{(This becomes PV in Step 2)}[/latex]

Step 2: Find [latex]FV_2[/latex].

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 20 \times 1 = 20\;\text{payments}[/latex]
[latex]I/Y = 9[/latex]
[latex]P/Y = 1[/latex]
[latex]C/Y = 1[/latex]
[latex]PMT = 0[/latex]
[latex]PV = \$255,\!540.6808[/latex]
[latex]CPT \;FV_\text{2} = \$1,\!432,\!154.943\; \text{(This becomes PV in Step 3)}[/latex]

Step 3: Find [latex]FV_3[/latex]

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 5 \times 1 = 5\;\text{payments}[/latex]
[latex]I/Y = 5[/latex]
[latex]P/Y = 1[/latex]
[latex]C/Y = 1[/latex]
[latex]PMT = 0[/latex]
[latex]PV = \$1,\!432,\!154.943[/latex]
[latex]CPT \;FV_\text{3} = \$1,\!827,\!832.95[/latex]

The maturity value of his RRSP is $1,827,832.95 when he turns 65.

11.3: Present Value of Annuities

1. When Sinbad retires, he expects his RRSP to pay him $2,000 at the end of every month for 25 years. If his retirement annuity earns 3.8% compounded quarterly, how much money does he need to have in his RRSP when he retires?

Solution:

Using BA2+ calculator:

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 25 \times 12 = 300\;\text{payments}[/latex]
[latex]I/Y = 3.8[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 4[/latex]
[latex]FV = 0[/latex]
[latex]PMT = -2,\!000[/latex]
[latex]CPT \;PV = \$387,\!444.19[/latex]

He needs to have $387,444.19 in the RRSP when he retires.

2. Sandy’s parents would like to have an annuity pay her $500 at the beginning of every month from September 1, 2012, to April 1, 2017, to help with her university tuition and living expenses. On May 1, 2017, they would like to give her a graduation gift of $5,000. If the annuity can earn 6.15% compounded quarterly, how much money must be in the account on September 1, 2012? (Use years and months in the calculations).

Solution:

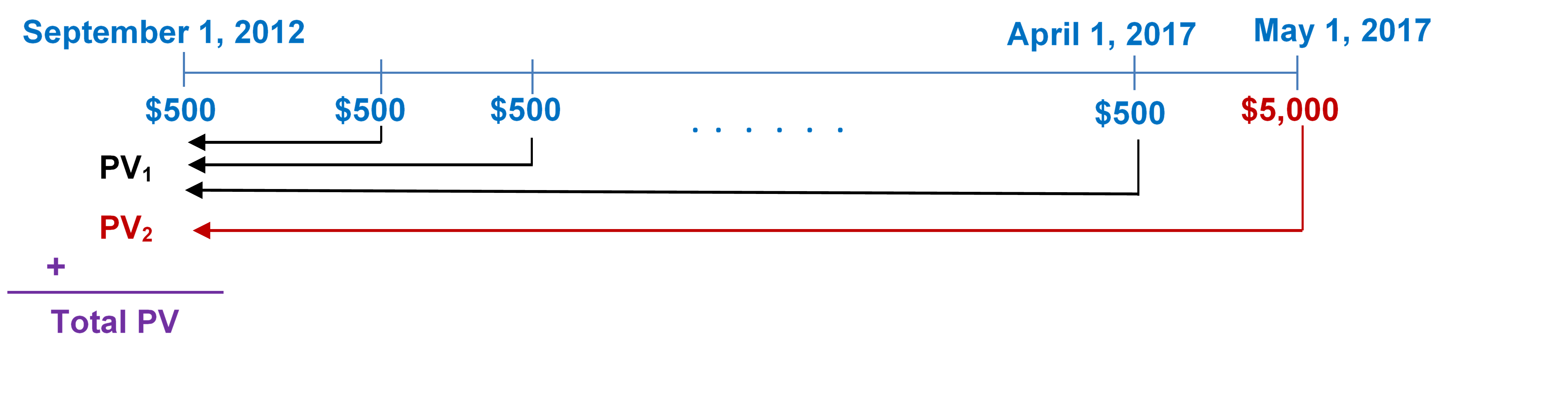
[latex]\text{Number of Years} = (\text{May}\; 1, 2017) – (\text{September}\; 1, 2012) = 4\frac{8}{12}[/latex]

Compute Total PV:

Using BA2+ calculator:

Mode = BGN

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 4\frac{8}{12} \times 12 = 56\;\text{payments}[/latex]
[latex]I/Y = 6.5[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 4[/latex]
[latex]PMT = -500[/latex]
[latex]FV = -5,\!000[/latex]
[latex]CPT \;PV = \$28,\!188.43[/latex]

 $28,188.43 must be in the account on September 1, 2012.

11.4: Annuity Payment Amounts

1. To save approximately $30,000 for a down payment on a home four years from today, what amount needs to be invested at the end of every month at 4.5% compounded semi-annually?

Solution:

Using BA2+ calculator:

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 4 \times 12 = 48\;\text{payments}[/latex]
[latex]I/Y = 4.5[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 0[/latex]
[latex]FV = 30,\!000[/latex]
[latex]CPT \;PMT = \$572.08[/latex]

The required end of month deposit is $572.08

2. Sinclair does not believe in debt and will only pay cash for all purchases. He has already saved up $140,000 toward the purchase of a new home with an estimated cost of $300,000. Suppose his investments earn 7.5% compounded monthly. How much does he need to contribute at the beginning of each quarter if he wants to purchase his home in five years?

Solution:

Using BA2+ calculator:

Mode = BGN

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 5 \times 4 = 20\;\text{payments}[/latex]
[latex]I/Y = 7.5[/latex]
[latex]P/Y = 4[/latex]
[latex]C/Y = 12[/latex]
[latex]PV = -140,\!000[/latex]
[latex]FV = 300,\!000\;\text{(Opposite sign to PV)}[/latex]
[latex]CPT \;PMT = -\$3,\!943.82[/latex]

The required beginning of quarter deposit is $3,943.82.

3. The Kowalskis’ only child is eight years old. They want to start saving into an RESP such that their son will be able to receive $5,000 at the end of every quarter for four years once he turns 18 and starts attending postsecondary school. When the annuity is paying out, it is forecast to earn 4% compounded monthly. While they make contributions at the end of every month to the RESP, it will earn 8% compounded semi-annually. Additionally, at the end of every year of contributions the government places a $500 grant into the RESP. What is the monthly contribution payment by the Kowalskis?

Solution:

Step 1: Calculate the present value of the payments to the child to determine the money needed in the RESP when he turns 18.

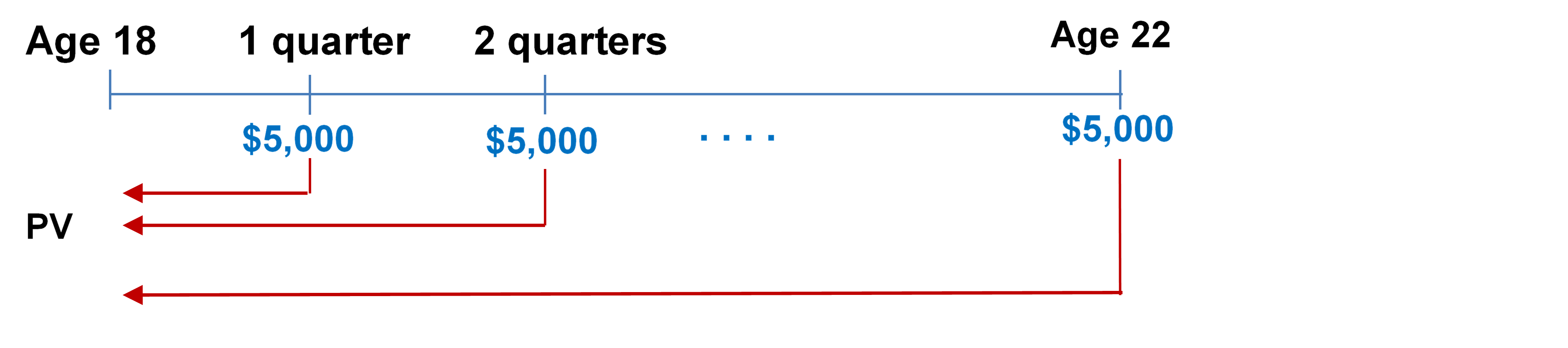
Using BA2+ calculator:

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 4 \times 4 = 16\;\text{payments}[/latex]
[latex]I/Y = 4[/latex]
[latex]P/Y = 4[/latex]
[latex]C/Y = 12[/latex]
[latex]PMT = -5,\!000[/latex]
[latex]FV = 0[/latex]
[latex]CPT \;PV = \$73,\!569.21991[/latex]

Step 2: Calculate the future value of the RESP grant at age 18.

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 10\times 1 = 10\;\text{payments}[/latex]
[latex]I/Y = 8[/latex]
[latex]P/Y = 1[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 0[/latex]
[latex]PMT = -500[/latex]
[latex]CPT \;FV = \$7,\!298.548671[/latex]

Step 3: Calculate the payments required from 8 years old to 18 years old.

Required FV = $73,569.21991 − $7,298.548671 = $66,270.67124

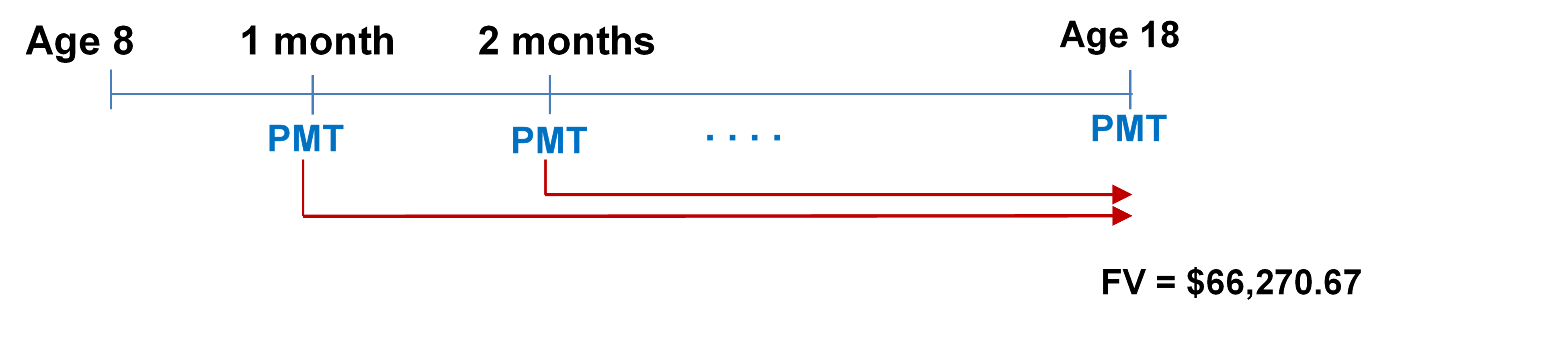
Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 10\times 12= 120\;\text{payments}[/latex]
[latex]I/Y = 8[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 0[/latex]
[latex]FV = -66,\!270.67[/latex]
[latex]CPT \;PMT = -\$364.88[/latex]

Therefore, a monthly deposit of $364.88 is required from age 8 to 18.

11.5: Number of Annuity Payments

1. Amarjit wants to save up for a down payment on his first home. A typical starter home in his area sells for $250,000 and the bank requires a 10% down payment. If he starts making $300 month-end contributions to an investment earning 4.75% compounded monthly, how long will it take for Amarjit to have the necessary down payment?

Solution:

Required future down payment = 10% × $250,000 = $25,000.

Using BA2+ calculator:

Mode = END

[latex]I/Y =4.75[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 12[/latex]
[latex]PMT = -300[/latex]
[latex]PV = 0[/latex]
[latex]FV = 25,\!000[/latex]
[latex]CPT \;N =72.161266\; \text{rounded up to}\; 73\; \text{monthly payments}[/latex]

[latex]\begin{align} \text{Number of years} &= \frac{73}{12}\\ &= 6.08\overline{3}\\ &= 6\;\text{years and}\; 0.08\overline{3}\times 12 = 1\;\text{month} \end{align}[/latex]

6 years, 1 month

2. Hi-Tec Electronics is selling a 52″ LG HDTV during a special “no sales tax” event for $1,995 with end of month payments of $100 including interest at 15% compounded semi-annually. How long will it take a consumer to pay off her new television?

 Solution:

Mode = END

[latex]I/Y =15[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 1,\!995[/latex]
[latex]PMT = -100[/latex]
[latex]FV = 0[/latex]
[latex]CPT \;N =22.9783316\; \text{rounded up to}\; 23\; \text{monthly payments}[/latex]

[latex]\begin{align} \text{Number of years} &= \frac{23}{12}\\ &= 1.91\overline{6}\\ &= 1\;\text{year and}\; 0.91\overline{6}\times 12 = 11\;\text{month} \end{align}[/latex]

1 year, 11 months

3. Most financial institutions tout the benefits of “topping up” your mortgage payments—that is, increasing from the required amount to any higher amount. Assume a 25-year mortgage for $200,000 at a fixed rate of 5% compounded semi-annually.
   a) How many fewer payments does it take to pay off your mortgage if you increased your monthly payments by 10%?
   b) How much money is saved by “topping up” the payments? Assume that all payments are equal amounts in your calculations.

Solution:

a)

Step 1: Find the original PMT.

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 25\times 12= 300\;\text{payments}[/latex]
[latex]I/Y = 5[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 200,\!000[/latex]
[latex]FV = 0[/latex]
[latex]CPT \;PMT = -\$1,\!163.21[/latex]

Therefore, the original PMT is $1,163.21. 

Step 2: Find the “Topped up” PMT.

“Topped up” PMT = $1,163.21(1.10) = $1,279.53

Step 3: Find the new term with the “Topped up” PMT.

Mode = END

[latex]I/Y =5[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 200,\!000[/latex]
[latex]PMT = -1,\!279.53[/latex]
[latex]CPT \;N =251.3724\; \text{rounded up to}\; 252\;\text{monthly payments}[/latex]

Step 4: How many fewer payments = 300 − 252 = 48

There are 48 fewer monthly payments. The mortgage is paid off four years earlier (after 21 years rather than 25 years).

b) 

Regular payments = 300 × $1,163.21 = $348,963
Topped up payments = 252 × $1,279.53 = $322,441.56
Savings = $348,963 − $322,441.56
Savings = $26,521.44

11.6: Annuity Interest Rates

1. Francisco just changed occupations. Unfortunately, he is not able to transfer his company pension with him to his new company. The administrators of the pension plan offer him the choice of a lump-sum payout of $103,075 today or beginning-of-month payments of $535 for the next 25 years. What semi-annually compounded rate of return are the pension administrators using in their calculations?

Solution:

Mode = BGN

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 25\times 12= 300\;\text{payments}[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 103,\!075[/latex]
[latex]FV = 0[/latex]
[latex]PMT = -535[/latex]
[latex]CPT \;I/Y = 3.9019[/latex]

3.9019% compounded semi-annually.

2. An investment today requires $1,125.51 to purchase. In return, the investment pays out $30 after every six months for the next 20 years, along with an additional final lump-sum payout of $1,000. What semi-annually compounded interest rate is being earned on the investment?

Solution:

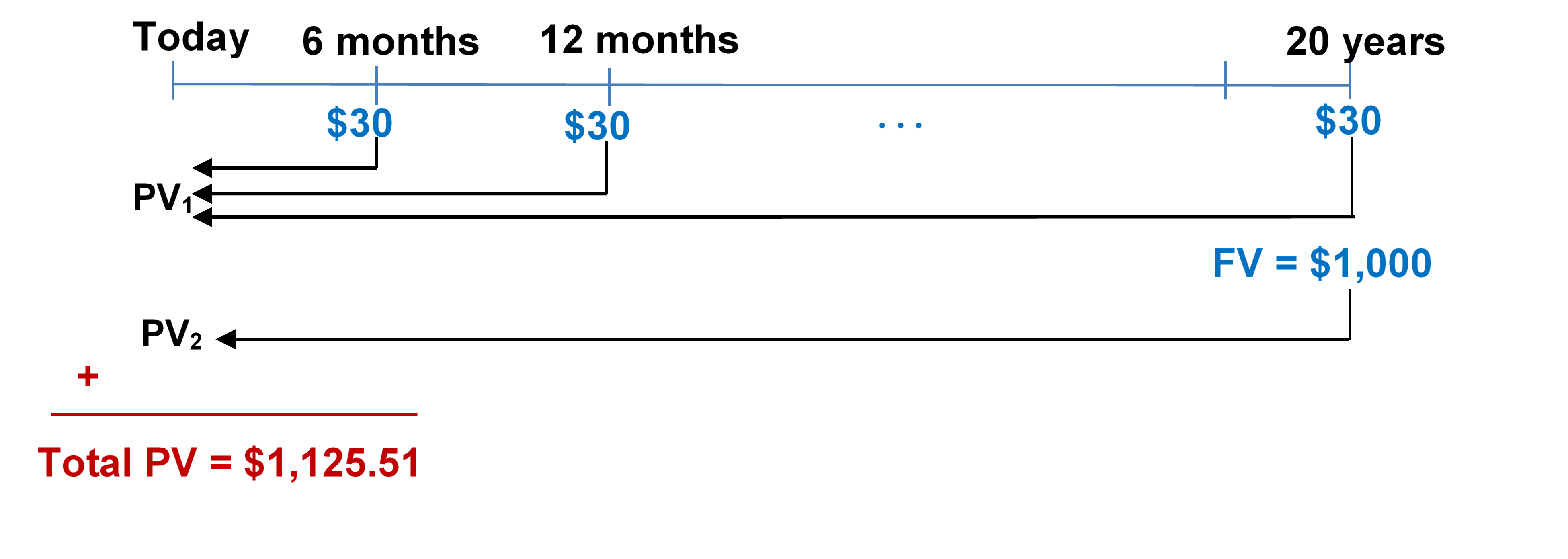
Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 20\times 2= 40\;\text{payments}[/latex]
[latex]P/Y = 2[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 1,\!125.51[/latex]
[latex]PMT = -30\;\text{(Opposite sign to PV)}[/latex]
[latex]FV = -1,\!000\;\text{(Opposite sign to PV)}[/latex]
[latex]CPT \;I/Y = 5.0000[/latex]

5% compounded semi-annually.

3. When you buy a car, a cash rebate is usually available if you finance the vehicle through your bank instead of the dealership; if you finance the vehicle through the dealership, you are not eligible for the cash rebate. Assume you can purchase a vehicle for $24,960 and finance it for four years with month-end payments at 0% through the dealership. Alternatively, you could get a loan from a bank and pay cash for your vehicle, which would entitle you to receive a $3,500 cash rebate. What monthly compounded interest rate would the bank have to charge to arrive at the same monthly payment as the dealership alternative? What decision rule can you create from this calculation?

Solution:

Finance Though Dealership:

Determine dealership payment:
If I/Y = 0%, then PMT = PV ÷ N  = $24,960 ÷ (12 × 4) = $520

Finance Though Bank:

The PV is reduced by the rebate:
PV = $24,960 − $3,500 = $21,460

Find the monthly compounded interest rate that allows the same end of month payments of $520.

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 4\times 12= 48\;\text{payments}[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 12[/latex]
[latex]PV = 21,\!460[/latex]
[latex]PMT = -520\;\text{(Opposite sign to PV)}[/latex]
[latex]FV = 0[/latex]
[latex]CPT \;I/Y = 7.6118[/latex]

7.6118% compounded monthly

Decision rule:

If you can obtain a loan from the bank for less than 7.6118% compounded monthly, your payments would be lower, and you should borrow from the bank.  If unable to obtain a rate lower than 7.6118% from the bank, forego the cash rebate and use the dealership financing.

Image Descriptions

Figure 11.1.1: Timeline showing monthly payments of $81,253.45 at the end of every month from now until 1 year. The FV of sum of all the payments at 1 year is $1,000,000  [Back to Figure 11.1.1]

Figure 11.1.2: Timeline showing quarterly payments of $1000 at the end of every quarter from now until 5 years. The FV of sum of all the payments at 5 years is $20,979.12 [Back to Figure 11.1.2]

Figure 11.1.3: Timeline showing monthly payments of $22.41 at the beginning of every month from now until 2 years. The PV of sum of all the payments at now is $500 [Back to Figure 11.1.3]

Figure 11.2.4: Timeline showing end of month payments of $400 from age 20 to age 40 at 9% compounded annually moved to age 40 to give FV₁. No deposits from age 40 to age 60 with FV₁ at age 40 moving to FV₂ at age 60 at 9% compounded annually. No deposits from age 60 to age 65 with FV₂ at age 60 moving to FV₃ at age 65 at 5% compounded annually. [Back to Figure 11.2.4]

Figure 11.3.1: Timeline showing $2000 at the end of every month for 25 years. The first $2000 occurs one month after retirement. The stream of $2000 monthly payments are brought back to the retirement date. [Back to Figure 11.3.1]

Figure 11.3.2: Timeline showing Payments of $500 at the beginning of every month from September 1, 2012 to April 1, 2017, all bought back to September 1, 2012 as PV₁. $5000 at May 1, 2017 brought back to September 1, 2012 as PV₂. At September 1, 2012, PV₁ + PV₂ equals Total PV. [Back to Figure 11.3.2]

Figure 11.4.1: Timeline showing PMT at the end of every month from today until 4 years. All PMTs moved to 4 years as FV. FV at 4 years equals $30,000. [Back to Figure 11.4.1]

Figure 11.4.2: Timeline showing PMT at the beginning of every quarter from today until 5 years. All PMTs moved to 5 years as FV₁. PV = $140,000 at today moved to 5 years as FV₂. FV₁ plus FV₂ at 5 years equals Total FV =$300,000. [Back to Figure 11.4.2]

Figure 11.4.3-1: Timeline showing $5000 at the end of every quarter from age 18 to age 22. All the $5000’s brought back to age 18 as PV. [Back to Figure 11.4.3-1]

Figure 11.4.3-2: Timeline showing $500 at the end of every year from age 8 to age 18. All the $500’s brought to age 18 as FV. [Back to Figure 11.4.3-2]

Figure 11.4.3-3: Timeline showing PMT at the end of every month from age 8 to age 18. All the PMT’s brought to age 18 as FV = $66,270.67. [Back to Figure 11.4.3-3]

Figure 11.6.2: Timeline showing $30 at the end of every 6 months from today until 20 years. All $30s moved back to today as PV₁. FV = $1,000 at 20 years moved back to today as PV₂. PV₁ plus PV₂ at today equals Total PV =$1,125.51. [Back to Figure 11.6.2]