10.2: Application: Long Term Promissory Notes
Application: Long Term Promissory Notes
This section introduces the mathematics behind the sale of promissory notes between companies. A promissory note, more commonly called a note, is a written debt instrument that details a promise made by a buyer to pay a specified amount to a seller at a predetermined and specified time. If the debt allows for interest to accumulate, then it is called an interest-bearing promissory note. If there is no allowance for interest, then it is called a non-interest-bearing promissory note. When promissory notes extend more than one year, they involve compound interest instead of simple interest.
How It Works
Recall that in simple interest the sale of short-term promissory notes involved three steps. You use the same three step sequence for long-term compound interest promissory notes. On long-term promissory notes, a three-day grace period is not required, so the due date of the note is the same as the legal due date of the note.
Step 1: Draw a timeline, similar to the one on the next page, detailing the original promissory note and the sale of the note.
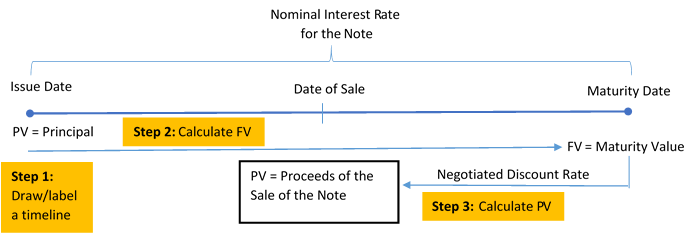
Step 2: At the stated nominal interest rate, take the initial principal on the date of issue and determine the note’s future value using the formula
[latex]FV=PV(1+i)^n[/latex]
Step 3: Using the date of sale, discount the maturity value of the note using a new negotiated discount rate of interest to determine the proceeds of the sale. This involves calculating the present value using the formula
[latex]\begin{align} PV&=\frac{FV}{(1+i)^n} \end{align}[/latex]
Important Notes
Two Interest Rates
The sale involves two interest rates: an interest rate tied to the note itself and an interest rate (the discount rate) used by the purchasing company to acquire the note. Do not confuse these two rates.
Example 10.2.1: Proceeds on an Interest Bearing Note
Assume that a three-year $5,000 promissory note with 9% compounded monthly interest is sold to a finance company 18 months before the due date at a discount rate of 16% compounded quarterly. What are the proceeds of the sale?
Solution:
Step 1: The timeline below illustrates the situation.
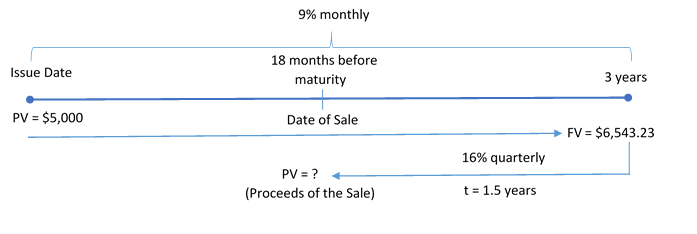
Step 2: Calculate the maturity value of the note at the end of the three-year term.
For the three-year term:
I/Y = 9%; C/Y = monthly = 12
[latex]i=\frac{I/Y}{C/Y}=\frac{9\%}{12}=0.75\%=0.0075[/latex]
[latex]n=C/Y \times \text{(Number of Years)}=12 \times 3 =36[/latex]
[latex]FV=\$5,\!000(1+0.0075)^{36}=\$6,\!543.23[/latex]
Step 3: Calculate the proceeds (PV) of the sale at 18 months before maturity. Discount the note back for 1.5 years.
I/Y = 16%; C/Y = quarterly = 4
[latex]i=\frac{I/Y}{C/Y}=\frac{16\%}{4}=4\%=0.04[/latex]
[latex]n=C/Y \times \text{(Number of Years)}=4 \times 1.5 =36[/latex]
[latex]\begin{align} PV&=\frac{FV}{(1+i)^n}\\ &=\frac{\$6,\!543.23}{(1+0.04)^6}\\ &=\$5,\!171.21 \end{align}[/latex]
The finance company purchases the note (invests in the note) for $5,171.21. Eighteen months later, when the note is paid, it receives $6,543.23.
Calculator instructions:
| Part | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Maturity | 36 | 9 | -5,000 | 0 | Answer: 6,543.226855 | 12 | 12 |
| Sale | 6 | 16 | Answer: -5,171.21 | 0 | 6,543.23 | 4 | 4 |
Important Notes
The assumption behind the three-step procedure for selling a long-term promissory note is that the process starts with the issuance of the note and ends with the proceeds of the sale. However, mathematically you may deal with any part of the transaction as an unknown. For example, perhaps the details of the original note are known, the finance company’s offer on the date of sale is known, but the quarterly discounted rate used by the finance company needs to be calculated.
The best strategy in any of these scenarios is always to execute step 1 and create a timeline. Identify the known variables to visualize the process, then solve for any variable(s) remaining unknown.
Example 10.2.2: Finding an Unknown Discount Rate
A $6,825 two-year promissory note bearing interest of 12% compounded monthly is sold six months before maturity to a finance company for proceeds of $7,950.40. What semi-annually compounded discount rate was used by the finance company?
Solution:
Step 1: The term, principal, promissory note interest rate, date of sale, and proceeds amount are known, as shown in the timeline.

Step 2: Calculate the maturity value of the note at the end of the two-year term.
For the two-year term:
I/Y = 12%; C/Y = monthly = 12
[latex]i=\frac{I/Y}{C/Y}=\frac{12\%}{12}=1\%=0.01[/latex]
[latex]n=C/Y \times \text{Number of Years}=12 \times 2 =24[/latex]
[latex]FV=\$6,\!825(1+0.01)^{24}=\$8,\!665.94[/latex]
Step 3: Using the future value formula, rearrange and solve for i.
Proceeds of the sale (PV) = $6,825; C/Y = semi-annually = 2
[latex]n=C/Y \times \text{(Number of Years)}=2 \times 0.5 =1[/latex]
[latex]\begin{align} FV&=PV(1+i)^n\\ \$8,\!665.94&=\$7,\!950.40{(1+i)^1}\\ 1.090000&=1+i\\ i&=0.090000 \end{align}[/latex]
Step 4: Using the formula for the periodic interest rate i rearrange and solve for I/Y.
[latex]\begin{align} i&=\frac{I/Y}{C/Y}\\ 0.09&=\frac{I/Y}{2}\\ I/Y&=0.090000 \times 2\\ &=0.18\; \text{or}\; 18\%\;\text{compounded semi-annually} \end{align}[/latex]
Calculator instructions:
| Part | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Maturity | 24 | 12 | -6,825 | 0 | Answer: 8,665.938976 | 12 | 12 |
| Discount Rate | 1 | Answer: 18.0001 | -7,950.40 | 0 | 8,665.94 | 2 | 2 |
The sale of the promissory note is based on a maturity value of $8,665.94. The finance company used a discount rate of 18% compounded semi-annually to arrive at proceeds of $7,950.40.
Non-Interest-Bearing Promissory Notes
A non-interest-bearing promissory note involves either truly having 0% interest or else already including a flat fee or rate within the note’s face value. Therefore, the principal amount and maturity amount of the promissory note are the same. Since the maturity value is known you can just use step 1 and step 3 to calculate the proceeds of the sale.
Concept Check:
Exercises
In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.
- Determine the proceeds of the sale on a six-year interest-bearing promissory note for $5,750 at 6.9% compounded monthly, discounted two years and three months before its due date at a discount rate of 9.9% compounded quarterly. (Answers: $6,972.52)
- A $36,555 interest-bearing note at 5% compounded monthly is issued on October 15, 2011, for a term of 87 months. Fifty-seven months later, the note is sold to yield a discount amount of $11,733.41. What quarterly compounded discount rate is being used? (Answer: 10.25% compounded quarterly)
- A seven-year interest-bearing note for $19,950 at 8.1% compounded quarterly is issued on January 19, 2006. Four years and 11 months later, the note is discounted at 14.55% compounded monthly. Determine the proceeds on the note and how much interest the original owner of the note realized.
(Answer: Proceeds are $25,874.62 and the interest realized is $5,924.62)
Timelines for the exercises are included in Solution to Exercises.
Image Descriptions
Figure 10.2.0: Timeline showing PV = Principal on the Issue Date. PV is brought (at the Nominal Interest Rate of the Note) to the Maturity Date as FV = Maturity Value. The FV at the Maturity Date is then brought back to the Date of Sale as PV = Proceeds of the Sale of the Note (at the Negotiated Discount Rate). Step 1: Draw/label a timeline. Step 2: Calculate FV. Step 3: Caculate PV. [Back to Figure 10.2.0]
Figure 10.2.1: Timeline showing PV = $5,000 on the Issue Date. PV is brought (at 9% monthly) to the 3 years as FV = $6,543.23. The FV at 3 years is then brought back to the Date of Sale (18 months before the maturity date) as PV = ? (Proceeds of the Sale) at 16% quarterly with t=1.5 years. [Back to Figure 10.2.1]
Figure 10.2.2: Timeline showing PV = $6,825 on the Issue Date. PV is brought (at 12% monthly) to 2 years as FV = ?. The FV at 2 years is then brought back to the Date of Sale (6 months before the maturity date) as PV = $7,950.40 (Proceeds of the Sale) at ?% semi-annually with t=0.5 years. [Back to Figure 10.2.2]

