9.4: Equivalent Payments
Equivalent Payments
This section explores the concept of equivalent payment streams. This involves equating two or more alternative financial streams to ensure that neither party is penalized by any choice. You then apply the concept of present value to loans and loan payments.
The Fundamental Concept of Equivalency
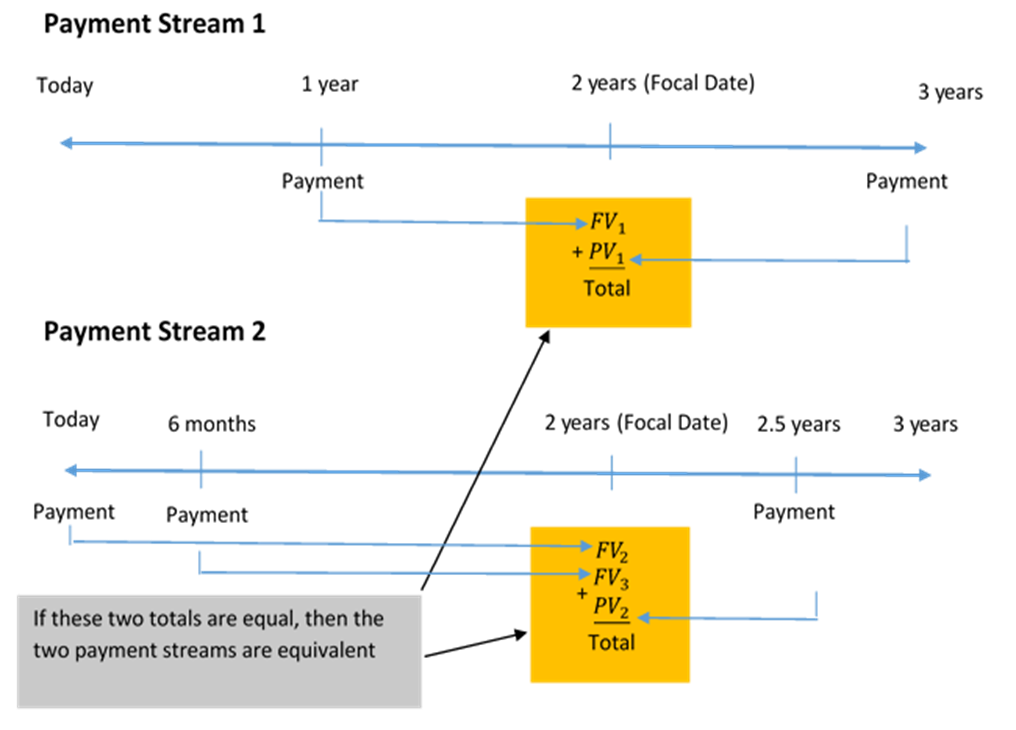
The fundamental concept of equivalency states that two or more payment streams are equal to each other if they have the same economic value on the same focal date. As illustrated in the figure, the two alternative financial streams are equivalent if the total of Payment Stream 1 is equal to the total of Payment Stream 2 on the same focal date. Note that the monies involved in each payment stream can be summed on the focal date because of the fundamental concept of time value of money.
How It Works
Follow these steps to solve an equivalent payment question:
Step 1: Draw as many timelines as needed to illustrate each of the original and proposed agreements. Clearly indicate dates, payment amounts, and the interest rate(s).
If you draw two or more timelines, align them vertically, ensuring that all corresponding dates are in the same columns. This allows you to see which payments need to be future valued and which need to be present valued to express them in terms of the chosen focal date.
Step 2: Choose a focal date to which all money will be moved. You should simplify your calculations by selecting a focal date corresponding to the date of an unknown variable.
Step 3: Calculate all needed periodic interest rates (i) using the formula
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compound per Year (C/Y)}}[/latex]
Step 4: Calculate the total number of compounds,(n) for each payment using the formula
[latex]n=(C/Y) \times (\text{Number of Years})[/latex]
Step 5: Perform the appropriate time value calculation for each payment using either the formula for FV or PV.
Step 6: Equate the values of the original and proposed agreements on the focal date and solve for any unknowns.
Example 9.4.1: Replacing a Payment Stream with a Single Payment
Assume you owe $1,000 today and $1,000 one year from now. You find yourself unable to make that payment today, so you indicate to your creditor that you want to make both payments six months from now instead. Prevailing interest rates are at 6% compounded semi-annually. What single payment six months from now (the proposed payment stream) is equivalent to the two payments (the original payment stream)?
Solution:
Step 1: The timeline illustrates the scenario.

I/Y = 6%; C/Y = semi-annually = 2
Step 2: Apply the fundamental concept of time value of money, moving all of the money to the same date. Since the proposed payment is for six months from now, you choose a focal date of six months.
Step 3: Calculate the periodic interest rate, i.
[latex]i=\frac{I/Y}{C/Y}=\frac{6\%}{2}=3\%[/latex].
Step 4: Calculate the total number of compounds, n.
[latex]n=C/Y \times (\text{Number of Years})=2\times\frac{1}{2}=1[/latex].
Step 5: Perform the appropriate time value calculations.
Moving today’s payment of $1,000 six months into the future, you have
[latex]FV=\$1,\!000(1+0.03)^1=\$1,\!030[/latex].
Moving the future payment of $1,000 six months earlier, you have
[latex]\begin{align} PV=\frac{\$1,\!000}{(1+0.03)^1}=\$970.87\end{align}[/latex].
| Payment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 6 | 1,000 | 0 | Answer: -$ 1,030 | 2 | 2 |
| 2 | 1 | 6 | Answer:-$970.87 | 0 | 1,000 | 2 | 2 |
Step 6: Now that money has been moved to the same focal date you can sum the two totals to determine the equivalent payment, which is $1,030 + $970.87 = $2,000.87. Note that this is financially fair to both parties. For making your $1,000 payment six months late, the creditor is charging you $30 of interest. Also, for making your second $1,000 payment six months early, you are receiving a benefit of $29.13. This leaves both parties compensated equitably: Neither party is financially better or worse off because of the change in the deal.
Example 9.4.2: Replacing a Payment Stream with a Single Payment
Johnson’s Garden Centre has recently been unprofitable and concludes that it cannot make two debt payments of $4,500 due today and another $6,300 due in three months. After discussions between Johnson’s Garden Centre and its creditor, the two parties agree that both payments could be made nine months from today, with interest at 8.5% compounded monthly. What total payment does Johnson’s Garden Centre need nine months from now to clear its debt?
Solution:
Step 1: The timeline illustrates the scenario.
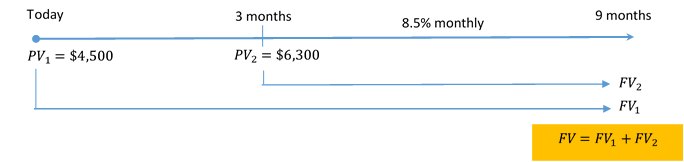
PV1 (today) = $4,500; PV2 (3 months from now) = $6,300; I/Y = 8.5%; C/Y = monthly = 12
Step 2: Due date for all payments = 9 months from today. This is your focal date.
Step 3: Calculate the periodic interest rate, i.
[latex]i=\frac{I/Y}{C/Y}=\frac{8.5\%}{12}=0.708\overline{3}\%=0.00708\overline{3}[/latex].
Step 4: Calculate the total number of compounds, n.
The first payment moves nine months into the future, or 9/12 of a year.
[latex]n=C/Y \times (\text{Number of Years})=12\times\frac{9}{12}=9[/latex].
The second payment moves six months into the future, or 6/12 of a year.
[latex]n=C/Y \times (\text{Number of Years})=12\times\frac{6}{12}=6[/latex].
Step 5: Perform the appropriate time value calculations.
Moving the first payment of $4,500 nine months into the future, you have
[latex]FV_1=\$4,\!500(1+0.00708\overline{3})^9=\$4,\!795.138902[/latex].
Moving the second payment of $6,300 six months into the future, you have
[latex]FV_2=\$6,\!300(1+0.007083\overline{3})^6=\$6,\!572.536425[/latex].
| Payment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 9 | 8.5 | 4,500 | 0 | Answer: -$ 4,795.138902 | 12 | 12 |
| 2 | 6 | 8.5 | 6,300 | 0 | Answer: -$ 6,572.526425 | 12 | 12 |
With interest, the two payments total $11,367.68. This is the $10,800 of the original principal plus $567.68 in interest for making the late payments.
Example 9.4.3: Replacing a Payment Stream with Multiple Payments
You have three debts to the same creditor: $3,000 due today, $2,500 due in 2¼ years, and $4,250 due in 3 years 11 months. Unable to fulfill this obligation, you arrange with your creditor to make two alternative payments: $3,500 in nine months and a second payment due in two years. You agree upon an interest rate of 9.84% compounded monthly. What is the amount of the second payment?
Solution:
Determine the amount of the second payment that is due two years from today. Apply the fundamental concept of time value of money, moving all money from the original and proposed payment streams to a focal date positioned at the unknown payment. Once all money is moved to this focal date, apply the fundamental concept of equivalence, solving for the unknown payment, or x.
With two payment streams and multiple amounts all on different dates, visualize two timelines. The payment amounts, interest rate, and due dates for both payment streams are known.
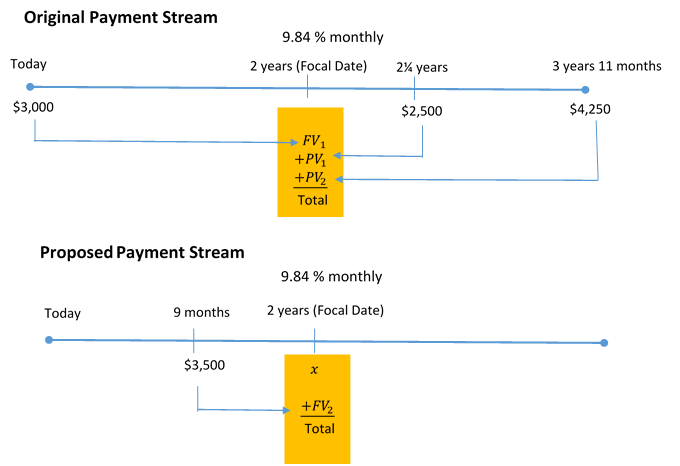
I/Y = 9.84%; C/Y = monthly = 12
Step 2: Focal Date = 2 years.
Step 3: Calculate the periodic interest rate, i.
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{9.84\%}{12}=0.82\%\;\text{or}\;0.0082[/latex]
Step 4: For each payment, calculate the number of compoundings per year by applying the formula
[latex]n=C/Y \times (\text{Number of Years})[/latex].
Step 5: For each payment, calculate the appropriate time value calculation. Note that all payments before the two year focal date require you to calculate future values, while all payments after the two-year focal date require you to calculate present values.
Steps 4 and 5: Using the circled number references from the timelines:
① [latex]n=12 \times 2 =24[/latex]; [latex]FV_1=\$3,\!000(1+0.0082)^{24}=\$3,\!649.571607[/latex]
② [latex]n=12 \times \frac{1}{4} =3[/latex]; [latex]\begin{align}PV_1=\frac{\$2,\!500}{1.0082^3}=\$2,\!439.494983\end{align}[/latex]
③ [latex]n=12 \times 1\frac{11}{12} =23[/latex]; [latex]\begin{align}PV_2=\frac{\$4,\!250}{1.0082^{23}}=\$3,\!522.207915\end{align}[/latex]
④ [latex]n=12 \times 1\frac{1}{4} =15[/latex]; [latex]FV_2=\$3,\!500(1+0.0082)^{15}=\$3,\!956.110749[/latex]
Step 6:
[latex]\begin{align} \$3,\!649.571607+\$2,\!439.494983+\$3,\!522.207915&=x+\$3,\!956.110749\\ \$9,\!611.274505&=x+\$3,\!956.110749\\ \$5,\!655.16&=x \end{align}[/latex]
| Calculation | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| ① | 24 | 9.84 | 3,000 | 0 | Answer: -$ 3,649.571607 |
12 | 12 |
| ② | 3 | 9.84 | Answer: -$ 2,439.494983 |
0 | 2,500 | 12 | 12 |
| ③ | 23 | 9.84 | Answer: -$ 3,522.207915 |
0 | 4,250 | 12 | 12 |
| ④ | 15 | 9.84 | 3,500 | 0 | Answer: -$ 3,956.110749 |
12 | 12 |
Exercises
In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.
- A winning lottery ticket offers the following two options:
a) A single payment of $1,000,000 today or
b) $250,000 today followed by annual payments of $300,000 for the next three years. If money can earn 9% compounded annually, which option should the winner select? How much better is that option in current dollars?
(Answers: a) $1,000,000; b) $9,388.40)
- James is a debt collector. One of his clients has asked him to collect an outstanding debt from one of its customers. The customer has failed to pay three amounts: $1,600 eighteen months ago, $2,300 nine months ago, and $5,100 three months ago. In discussions with the customer, James finds she desires to clear up this situation and proposes a payment of $1,000 today, $4,000 nine months from now, and a final payment two years from now. The client normally charges 16.5% compounded quarterly on all outstanding debts. What is the amount of the third payment? (Answer: $7,465.59)
- Four years ago, Aminata borrowed $5,000 from Randal with interest at 8% compounded quarterly to be repaid one year from today. Two years ago, Aminata borrowed another $2,500 from Randal at 6% compounded monthly to be repaid two years from today. Aminata would like to restructure the payments so that she can pay 15 months from today and 2½ years from today. The first payment is to be twice the size of the second payment. Randal accepts an interest rate of 6.27% compounded monthly on the proposed agreement. Calculate the amounts of each payment assuming the focal date is 15 months from today. (Answer: $7,232.96)
Timelines for the exercises are included in Solution to Exercises.
Image Descriptions
Figure 9.4.0: The figure illustrates that two alternative financial streams are equivalent if the total of Payment Stream 1 is equal to the total of Payment Stream 2 on the same focal date. Note that the monies involved in each payment stream can be summed on the focal date because of the fundamental concept of time value of money. [Back to Figure 9.4.0]
Figure 9.4.1: A timeline showing: $1,000 payment at Today moving forward to 6 months (Focal Date) as FV at 6% semi-annually. $1,000 payment at 1 year moving back to 6 months (Focal Date) as PV at 6% semi-annually. At 6 months (Focal Date), FV = $1,030 and PV = $970.87, and the sum of FV and PV is $2000.87. [Back to Figure 9.4.1]
Figure 9.4.2: Timeline: PV1= $4,500 at Today moving to 9 months as FV1. PV2 = $6,300 at 3 months moving to 9 months as FV2. At 9 months, FV = FV1 + FV2 [Back to Figure 9.4.2]
Figure 9.4.3: Original Payment Stream Timeline: $3000 at Today moving to 2 years (Focal Date) as FV1. $2500 at 2.25 years moving back to 2 years as PV1. $4,250 at 3 yeears, 11 months moving back to 2 years as PV2. At 2 years (Focal Date) FV1 + PV1 + PV2 = Total. 9.84% monthly through out. Proposed Payment Stream Timeline: $3,500 at 9 months moved to 2 years (Focal Date) as FV2. x at 2 years. At 2 years (Focal Date), x + FV2 = Total. 9.84% monthly throughout. [Back to Figure 9.4.3]

