11.2 Future Value of Annuities
Future Value of Annuities
The future value of any annuity equals the sum of all the future values for all of the annuity payments when they are moved to the end of the last payment interval. For example, assume you will make $1,000 contributions at the end of every year for the next three years to an investment earning 10% compounded annually. This is an ordinary simple annuity since payments are at the end of the intervals, and the compounding and payment frequencies are the same. If you wanted to know how much money you have in your investment after the three years, you would apply the fundamental concept of the time value of money to move each payment amount to the future date (the focal date) and sum the values to arrive at the future value.
The Formula
[latex]\colorbox{LightGray}{Formula 11.2A}\; \color{BlueViolet}{\text{Ordinary Annuity Future Value:}\; FV_{ORD}=PMT \left[\frac{(1+i)^n-1}{i}\right]}[/latex]
where,
PMT is the regular payment amount.
i is the periodic interest rate.
n is the total number of payments.
Important Notes
Calculating the periodic interest rate (i)
For ordinary simple annuities where the compounding interval equals the payment interval (P/Y = C/Y) you calculate the periodic rate (i) using the formula
[latex]i=\frac{I/Y}{C/Y}[/latex]
For ordinary general annuities where the compounding interval does not equal the payment interval (P/Y [latex]\ne[/latex] C/Y) you need to calculate the equivalent periodic rate (ieq) per payment interval using the formula
[latex]i_{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1[/latex]
where,
i is the given periodic rate.
C/Y is the number of compounds per year.
P/Y is the number of payments per year.
The future value formula for ordinary general annuities becomes
[latex]FV_{ORD}=PMT \left[\frac{(1+i_{eq})^n-1}{i_{eq}}\right][/latex]
How It Works
There is a five-step process for calculating the future value of any ordinary annuity:
Step 1: Identify the annuity type (simple or general). Draw a timeline to visualize the question.
Step 2: Identify the known variables, including PV, I/Y, C/Y, PMT, P/Y, and Years.
Step 3: Calculate the periodic interest rate (i). See Important Notes above.
Calculate the number of payments (n) using the formula
[latex]n= P/Y \times \text{(Number of Years)}[/latex]
Step 4: If PV = $0, proceed to step 5. If there is a nonzero value for PV, treat it like a single payment and calculate the future value using Formula 9.2.
[latex]FV_{(1)}=PV(1+i)^n[/latex]
Step 5: Apply Formula 11.2A to calculate the future value.
If you calculated a future value in step 4, combine the future values from steps 4 and 5 to arrive at the total future value.
Important Notes
Calculating the Interest Amount
For investment annuities, if you are interested in knowing how much of the future value is principal and how much is interest, you can use the formula
[latex]I=FV-\;\text{Total Contributions}\;=FV-(n \times PMT+PV)[/latex]
where PV is the initial contribution.
Your BAII Plus Calculator
Adapting your calculator skills to suit annuities requires three important changes:
- Enter your values for PV (if known) and PMT. Be sure to enter it with the correct cash flow sign convention. When you invest, the payment has the same sign as the PV. When you borrow, the sign of the payment is opposite that of PV.
- Enter your values for P/Y and C/Y separately. Access the function by pressing 2nd P/Y to find the following entry fields, through which you can scroll using your arrow buttons. To enter any information into one of these fields, scroll to the field on your screen, key in the data, and press Enter. When you enter a value into the P/Y field, the calculator will automatically copy the value into the C/Y field for you. If in fact the C/Y is different, you can change the number manually. To exit the P/Y window, press 2nd Quit.
Concept Check
Example 11.2.1: Future Value of an Investment Account
A financial adviser is reviewing one of her client’s accounts. The client has been investing $1,000 at the end of every quarter for the past 11 years in a fund that has averaged 7.3% compounded quarterly. How much money does the client have today in his account?
Solution:
Step 1: The payments are at the end of the payment intervals, and both the compounding period and the payment intervals are the same. This is an ordinary simple annuity. Calculate its value at the end, which is its future value, or FVORD.
The timeline shows the client’s account.

Step 2: PV = $0; I/Y = 7.3%; C/Y = 4; PMT = $1,000; P/Y = 4; Years = 11
Step 3: Calculate the periodic interest rate, i.
[latex]i=\frac{I/Y}{C/Y}=\frac{7.3\%}{4}=1.825\%[/latex]
Step 4: Skip this step since PV=$0.
Step 5: Apply Formula 11.2A to calculate the future value, FVORD.
n = P/Y × (Number of Years) = 4 × 11 =44
[latex]\begin{align} FV_{ORD}&=PMT \left[ \frac{(1+i)^n-1}{i}\right]\\ &=\$1,\!000 \left[ \frac{(1+0.01825)^{44}-1}{0.01825}\right]\\ &=\$66,\!637.03 \end{align}[/latex]
Therefore, FVORD = FV = $66,637.03
Calculator instructions:
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 44 | 7.3 | 0 | -1,000 | Answer: 66,637.03449 | 4 | 4 |
The figure shows how much principal and interest make up the final balance. After 11 years of $1,000 quarterly contributions, the client has $66,637.03 in the account.
Example 11.2.2: Future Value of a Savings Annuity (PV given)
A savings annuity already contains $10,000. If an additional $250 is invested at the end of every month at 9% compounded semi-annually for a term of 20 years, what will be the maturity value of the investment?
Solution:
Step 1: The payments are at the end of the payment intervals, and the compounding period and payment intervals are different P/Y [latex]\ne[/latex] C/Y. This is an ordinary general annuity. Calculate its value at the end, which is its future value, or FVORD.

Step 2: PV = 10,000; I/Y = 9%; C/Y = 2; PMT = $250; P/Y = 12; Years = 20
Step 3: Since P/Y [latex]\ne[/latex] C/Y, calculate the equivalent periodic rate, ieq.
[latex]i=\frac{I/Y}{C/Y}=\frac{9\%}{2}=4.5\%[/latex]
[latex]i{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.045)^{\frac{2}{12}}-1=0.007363123[/latex]
Step 4: Apply Formula 9.2A to calculate the future value, FV1.
Given information: PV = $10,000; n = P/Y × (Number of Years) = 12 × 20 = 240
[latex]FV_1=\$10,\!000(1+0.007363123)^{240}=\$58,\!163.64538[/latex]
Step 5: Apply Formula 11.2A to calculate the future value of the payments, FVORD.
[latex]\begin{align} FV_{ORD}&=PMT \left[ \frac{(1+i_{eq})^n-1}{i_{eq}}\right]\\ &=\$250 \left[ \frac{(1+0.007363123)^{240}-1}{0.007363123}\right]\\ &=\$163,\!529.9486 \end{align}[/latex]
Combine steps 4 and 5 to calculate the total future value, FV.
FV = $58,163.64538 + $163,529.9486 = $221,693.59
Calculator instructions:
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 240 | 9 | -10,000 | -250 | Answer: 221,693.5946 | 12 | 2 |
The figure shows how much principal and interest make up the final balance. The savings annuity will have a balance of $221,693.59 after the 20 years.
Important Notes
If any of the variables, including I/Y, C/Y, PMT, or P/Y change between the start and end point of the annuity, or if any additional single payment deposit or withdrawal is made, a new time segment is created and must be treated separately. There will then be multiple time segments that require you to work left to right by repeating steps 3 through 5 in the procedure. The future value at the end of one time segment becomes the present value in the next time segment.
Pay extra attention when the variable that changes between time segments is the payment frequency (P/Y). When inputted into a BAII+ calculator, the P/Y automatically copies across to the compounding frequency (C/Y). Unless your C/Y also changed to the same frequency, this means that you must scroll down to the C/Y window and re-enter the correct value for this variable, even if it didn’t change. The following example illustrates this concept.
Example 11.2.3: Saving Up for a Vacation
Genevieve has decided to start saving up for a vacation in two years, when she graduates from university. She already has $1,000 saved today. For the first year, she plans on making end-of-month contributions of $300 and then switching to end-of-quarter contributions of $1,000 in the second year. If the account can earn 5% compounded semi-annually in the first year and 6% compounded quarterly in the second year, how much money will she have saved when she graduates?
Solution:
Step 1: There is a change of variables after one year. As a result, you need a Year 1 time segment and a Year 2 time segment. In both segments, payments are at the end of the period. In Year 1, the compounding period and payment intervals are different. In Year 2, the compounding period and payment intervals are the same. This is an ordinary general annuity followed by an ordinary simple annuity. You aim to calculate the future value, FVORD.
The timeline for her vacation saving appears below.
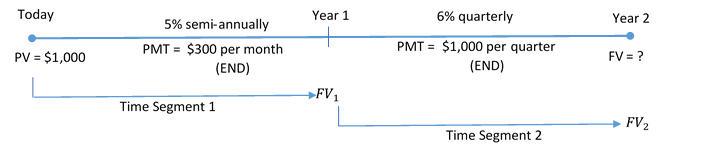
Step 2:
Time Segment 1: PV = $1,000; I/Y = 5%; C/Y = 2; PMT = $300; P/Y = 12; Years = 1
Time Segment 2: PV = FV1; I/Y = 6%; C/Y = 4; PMT = $1,000; P/Y = 4; Years = 1
For the first time segment:
Step 3: Since P/Y [latex]\ne[/latex] C/Y, calculate the equivalent periodic rate, ieq.
[latex]i=\frac{I/Y}{C/Y}=\frac{5\%}{2}=2.5\%[/latex]
[latex]i{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.025)^{\frac{2}{12}}-1=0.004123915[/latex]
Step 4: Apply Formula 9.2A to calculate the future value, FV(1).
Given information: PV = $1,000; n = P/Y × (Number of Years) = 12 × 1 = 12
[latex]FV_{(1)}=\$1,\!000(1+0.004123915)^{12}=\$1,\!050.625[/latex]
Step 5: Apply Formula 11.2A to calculate the future value of the payments.
[latex]\begin{align} FV_{ORD_1}&=PMT \left[ \frac{(1+i_{eq})^n-1}{i_{eq}}\right]\\ &=\$300 \left[ \frac{(1+0.004123915)^{12}-1}{0.004123915}\right]\\ &=\$3,\!682.786451 \end{align}[/latex]
Calculate the total future value, FV1.
FV1 = $1,050.625 + $3,682.786451 = $4,733.411451
This becomes PV for the second time segment.
For the second time segment:
Step 3: Since P/Y = C/Y, calculate the periodic rate, i.
[latex]i=\frac{I/Y}{C/Y}=\frac{6\%}{4}=1.5\%[/latex]
Step 4: Apply Formula 9.2A to calculate the future value, FV(2).
PV = $4,733.411442 = FV1; n = P/Y × (Number of Years) = 4 × 1 = 4
[latex]FV_{(2)}=PV(1+i)^n=\$4,\!733.411442(1+0.015)^{4}=\$5,\!023.870384[/latex]
Step 5: Apply Formula 11.2A to calculate the future value of the payments.
[latex]\begin{align} FV_{ORD_2}&=PMT \left[ \frac{(1+i)^n-1}{i}\right]\\ &=\$1,\!000 \left[ \frac{(1+0.015)^{4}-1}{0.015}\right]\\ &=\$4,\!090.903375 \end{align}[/latex]
Combine steps 4 and 5 to calculate the total future value, FV2.
FV2 = $5,023.870384 + $4,090.903375 = $9,114.77
Therefore, FV2 = FV = $9,114.77
Calculator instructions:
| Time segment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 12 | 5 | -1,000 | -300 | Answer: 4,733.411451 | 12 | 2 |
| 2 | 4 | 6 | -4,733.411451 | -1,000 | Answer: 9,114.773759 | 4 | 4 |
The figure shows how much principal and interest make up the final balance. When Genevieve graduates she will have saved $9,114.77 toward her vacation.
Annuities Due
An annuity due occurs when payments are made at the beginning of the payment interval.
The Formula
[latex]\colorbox{LightGray}{Formula 11.2B}\; \color{BlueViolet}{\text{Annuity Due Future Value:}\; FV_{DUE}=PMT \left[\frac{(1+i)^n-1}{i}\right]\times(1+i)}[/latex]
We see that the future value of an annuity due is simply (1+i) times the future value of an ordinary annuity.
How It Works
The steps required to solve for the future value of an annuity due are almost identical to those you use for the ordinary annuity. The only difference lies in step 5, where you use Formula 11.2B instead of Formula 11.2A.
Using Your BAII Plus Calculator

To adapt your calculator to an annuity due, you must toggle the payment timing setting from END to BGN. The calculator default is END, which is the ordinary annuity. The payment timing setting is found on the second shelf above the PMT key (because it is related to the PMT!). To toggle the setting, complete the following sequence:
2nd BGN 2nd SET 2nd Quit
When the calculator is in annuity due mode, a tiny BGN appears in the upper right-hand corner of your calculator. To return the calculator to ordinary mode, repeat the above keystrokes.
Concept Check
Example 11.2.4: Lottery Winnings
The Set for Life instant scratch n’ win ticket offers players a chance to win $1,000 per week for the next 25 years starting immediately upon validation. If a winner was to invest all of his money into an account earning 5% compounded annually, how much money would he have at the end of his 25-year term? Assume each year has exactly 52 weeks.
Solution:
Step 1: The payments start immediately, and the compounding period and payment intervals are different. Therefore, this a general annuity due. Calculate its value at the end, which is its future value, or FVDUE.
The timeline for the lottery savings is below.

Step 2: PV = $0; I/Y = 5%; C/Y = 1; PMT = $1,000; P/Y = 52; Years = 25
Step 3: Since P/Y [latex]\ne[/latex] C/Y, calculate the equivalent periodic rate (ieq) that matches the payment interval.
[latex]i=\frac{I/Y}{C/Y}=\frac{5\%}{1}=5\%[/latex]
[latex]i{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.05)^{\frac{1}{52}}-1=0.000938713\;\text{per week}[/latex]
Step 4: Since there is no PV, skip this step.
Step 5: Apply Formula 11.2B to calculate the future value of the payments, FVDUE.
n = P /Y × (Number of Years) = 52 × 25 = 1300
[latex]\begin{align} FV_{DUE}&=PMT \left[ \frac{(1+i_{eq})^n-1}{i_{eq}}\right]\times(1+i_{eq})\\ &=\$1.\!000 \left[ \frac{(1+0.000938713)^{1300}-1}{0.000938713}\right](1+0.000938713)\\ &=\$2,\!544,\!543.218 \end{align}[/latex]
Therefore, FVDUE = FV = $2,544,543.22
Calculator instructions:
| Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | 1300 | 5 | 0 | -1000 | Answer: 2,544,543.218 | 52 | 1 |
The figure shows how much principal and interest make up the final balance. If the winner was to invest all of his lottery prize money, he would have $2,544,543.22 after 25 years.
Example 11.2.5: Saving into a Trust with a Variable Change
When Roberto’s son was born, Roberto started making payments of $1,000 at the beginning of every six months to a trust fund earning 5.75% compounded monthly. After five years, he changed his contributions and started depositing $500 at the beginning of every quarter. How much money will be in his son’s trust fund when his son turns 18?
Solution:
Step 1: There is a change of variables after five years. As a result, you need two time segments. In both segments, payments are at the beginning of the period and the compounding periods and payment intervals are different. Therefore, Roberto has two consecutive general annuities due. Combined, calculate the future value, or FVDUE.
The timeline for the trust fund is shown below.
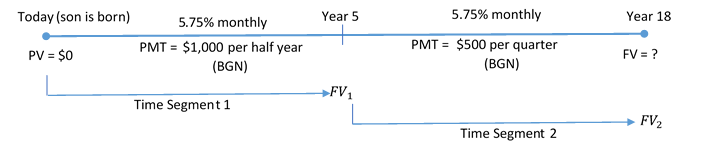
Step 2:
Time segment 1: PV = $0; I/Y = 5.75%; C/Y = 12; PMT = $1,000; P/Y = 2; Years = 5
Time segment 2: PV = FV1; I/Y = 5.75%; C/Y = 12; PMT = $500; P/Y = 4; Years = 13
For the first time segment:
Step 3: Since P/Y [latex]\ne[/latex]C/Y, calculate the equivalent periodic rate, ieq.
[latex]i=\frac{I/Y}{C/Y}=\frac{5.75\%}{12}=0.4719\overline{6}\%[/latex]
[latex]i{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.004719\overline{6})^{\frac{12}{2}}-1=0.029096609[/latex]
Step 4: Since the is no PV skip this step.
Step 5: Apply Formula 11.2B to calculate the future value.
n = P/Y × (Number of Years) = 2 × 5 = 10
[latex]\begin{align} FV_{DUE_1}&=PMT \left[ \frac{(1+i_{eq})^n-1}{i_{eq}}\right]\times(1+i_{eq})\\ &=\$1,\!000 \left[ \frac{(1+0.029096609)^{10}-1}{0.029096609}\right]\times(1+0.029096609)\\ &=\$11,\!748.47466=FV_1 \end{align}[/latex]
This becomes PV for the second time segment.
For the second time segment:
Step 3: Since P/Y [latex]\ne[/latex]C/Y, calculate the equivalent periodic rate, ieq.
[latex]i\;\text{remains unchanged}\;=0.4719\overline{6}\%[/latex]
[latex]i{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.004719\overline{6})^{\frac{12}{4}}-1=0.01444399[/latex]
Step 4: Apply Formula 9.2A to calculate the future value, FV(2).
Given information: PV = $11,748.47466 = FV_1;
n = P/Y × (Number of Years) = 4 × 13 = 52
[latex]FV_{(2)}=PV(1+i_{eq})^n=\$11,\!748.47466(1+0.01444399)^{52}=\$24,\!765.17[/latex]
Step 5: Apply Formula 11.2B to calculate the future value of the payments.
[latex]\begin{align} FV_{DUE_2}&=PMT \left[ \frac{(1+i_{eq})^n-1}{i_{eq}}\right]\times(1+i_{eq})\\ &=\$500 \left[ \frac{(1+0.01444399)^{52}-1}{0.01444399}\right]\times(1+0.01444399)\\ &=\$38,\!907.21529 \end{align}[/latex]
Combine steps 4 and 5 to calculate the total future value, FV2.
FV2 = $24,765.17 + $38,907.21529 = $63,672.38529
Therefore, FV2 = FV = $63,672.39
Calculator instructions:
| Time segment | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| 1 | BGN | 10 | 5.75 | 0 | -1,000 |
Answer: 11,748.47466 |
2 | 12 |
| 2 | BGN | 52 | 5.75 | -11,748.47466 | -500 |
Answer: 63,672.385 29 |
4 | 12 |
The figure shows how much principal and interest make up the final balance. When Roberto’s son turns 18, the trust fund will have a balance of $63,672.39.
Exercises
In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.
- You are a financial adviser. Your client is thinking of investing $600 at the end of every six months for the next six years with the invested funds earning 6.4% compounded semi-annually. Your client wants to know how much money she will have after six years. What do you tell your client? (Answer: $8,612.62)
- McDonald’s major distribution partner, The Martin-Brower Company, needs at least $1 million to build a new warehouse in Medicine Hat two years from today. To date, it has invested $500,000. If it continues to invest $50,000 at the end of every quarter into a fund earning 6% quarterly, will it have enough money to build the warehouse two years from now? Show calculations to support your answer.
(Answer: No, the fund is $15,111.75 short of the money required.)
- The Saskatchewan Roughriders started a rainy-day savings fund three-and-a-half years ago to help pay for stadium improvements. At the beginning of every quarter the team has deposited $20,000 into the fund, which has been earning 4.85% compounded semi-annually. How much money is in the fund today? (Answer: $306,680.93)
- Carlyle plans to make month-end contributions of $400 to his RRSP from age 20 to age 40. From age 40 to age 65, he plans to make no further contributions to his RRSP. The RRSP can earn 9% compounded annually from age 20 to age 60, and then 5% compounded annually from age 60 to age 65. Under this plan, what is the maturity value of his RRSP when he turns 65? (Answer: $1,827,832.95)
Timeline for exercise 4 is included in Solution to Exercises.
Image Descriptions
Figure 11.2.1: Timeline showing PV = $0 11 years ago. FV = ? Today. 7.3% quarterly. PMT = $1,000 per quarter (END) [Back to Figure 11.2.1]
Figure 11.2.2: Timeline showning PV = $10,000 Today. FV = ? in 20 years. 9% semi-annually. PMT = $250 per month (END) [Back to Figure 11.2.2]
Figure 11.2.3: Timeline showing PV = $1,000 at Today moving to Year 1 as FV1. Time Segment 1 with 5% semi-annually and PMT = $300 per month (END). FV1 at Year 1 moving to Year 2 as FV2. Time Segment 2 with 6% quarterly and PMT = $1,000 per quarter (END). [Back to Figure 11.2.3]
Figure 11.2.C: BAII Plus Calculator identifying BGN (will appear when in annuity due mode). Exit the Window, Toggle the Setting and Payment Time Button identified. [Back to Figure 11.2.C]
Figure 11.2.4: Timeline showing PV = $0 at Today. FV = ? in 25 years. 5% annually. PMT = $1,000 per week (BGN) [Back to Figure 11.2.4]
Figure 11.2.5: Timeline showing PV = $0 at Today (son is born) moving to Year 5 as FV1. Time Segment 1 with 5.75% monthly and PMT = $1,000 per half year (BGN). FV1 at Year 5 moving to Year 18 as FV2. Time Segment 2 with 5.75% monthly and PMT = $1,000 per quarter (BGN). [Back to Figure 11.2.5]
An annuity in which the payment interval equals the compounding interval, and payments are made at the term.
An annuity in which the payment interval does not equal the compounding interval, and payments are made at the end of the term.

