9.5 Determining the Interest Rate
Determining the Interest Rate
This section shows how to calculate the nominal interest rate on single payments when you know both the future value and the present value.
How It Works
Follow these steps to solve for the nominal interest rate on a single payment:
Step 1: Draw a timeline to help you visualize the question. Of utmost importance is identifying the values of PV and FV, the number of years involved, and the compounding for the interest rate.
Step 2: Calculate the number of compounds (n) using the formula
[latex]n=C/Y \times\text{(Number of Years)}[/latex].
Step 3: Substitute known variables into the formula FV = PV(1+i)n rearrange and solve for the periodic interest rate, i.
[latex]i=\left(\frac{FV}{PV}\right)^{\frac{1}{n}}-1[/latex]
Step 4: Substitute the periodic interest rate and the compounding frequency into the formula [latex]i=\frac{I/Y}{C/Y}[/latex] rearrange, and solve for the nominal interest rate, I/Y.
[latex]I/Y=i \times C/Y[/latex]
Ensure that the solution is expressed with the appropriate compounding words.
Important Notes
Handling Decimals in Interest Rate Calculations
Rule 1: A Clear Marginal Effect
Use this rule when it is fairly obvious how to round the interest rate. The dollar amounts used in calculating the interest rate are rounded by no more than a half penny. Therefore, the calculated interest rate should be extremely close to its true value. For example, if you calculate an I/Y of 7.999884%, notice this value would have a marginal difference of only 0.000116% from a rounded value of 8%. Most likely the correct rate is 8% and not 7.9999%. However, if you calculate an I/Y of 7.920094%, rounding to 8% would produce a difference of 0.070006%, which is quite substantial. Applying marginal rounding, the most likely correct rate is 7.92% and not 7.9201%, since the marginal impact of the rounding is only 0.000094%.
Rule 2: An Unclear Marginal Effect
Use this rule when it is not fairly obvious how to round the interest rate. For example, if the calculated I/Y = 7.924863%, there is no clear choice of how to round the rate. In these cases or when in doubt, apply the standard rule established for this book of rounding to four decimals. Hence, I/Y = 7.9249% in this example.
It is important to stress that the above recommendations for rounding apply to final solutions. If the calculated interest rate is to be used in further calculations, then you should carry forward the unrounded interest rate.
Your BAII Plus Calculator
Enter values for the known variables, PV, FV, N, and both of the values in the P/Y window (P/Y and C/Y) following the procedures established in Section 9.2. Ensure proper application of the cash flow sign convention to PV and FV. One number must be negative while the other is positive, otherwise an ERROR message will appear on your calculator display.
Example 9.5.1: Finding the Nominal Rate
When Sandra borrowed $7,100 from Sanchez, she agreed to reimburse him $8,615.19 three years from now including interest compounded quarterly. What nominal quarterly compounded rate of interest is being charged?
Solution:
Step 1: The present value, future value, term, and compounding are known, as illustrated in the timeline.

PV = $7,100; FV = $8,615.19; C/Y = quarterly = 4; Term = 3 years
Step 2: Calculate the total number of compoundings, n.
[latex]n=C/Y \times \text{(Number of Years)}=4 \times 3=12[/latex]
Step 3: Calculate the periodic rate, i.
[latex]\begin{align} FV&=PV(1+i)^n\\ \$8,\!615.19&=\$7,\!100(1+i)^{12}\\ 1.213407&=(1+i)^{12}\\ 1.213407^{\frac{1}{12}}&=1+i\\ 1.01624996&=1+i\\ i&=0.01624996 \end{align}[/latex]
Step 4: Calculate the nominal rate, I/Y.
[latex]\begin{align} i&=\frac{I/Y}{C/Y}\\ 0.01624996&=\frac{I/Y}{4}\\ I/Y&=0.06499985=0.065\;\text{or}\;6.5\%\;\text{(compounded quarterly)} \end{align}[/latex]
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 12 | Answer: 6.499985 | -7,100 | 0 | 8,615.19 | 4 | 4 |
Sanchez is charging an interest rate of 6.5% compounded quarterly on the loan to Sandra.
Example 9.5.2: Known Interest Amount
Five years ago, Taryn placed $15,000 into an RRSP that earned $6,799.42 of interest compounded monthly. What was the nominal interest rate for the investment?
Solution:
Step 1: The present value, interest earned, term, and compounding are known, as illustrated in the timeline.

FV = $15,000 + $6,799.42 = $21,799.42; PV = $15,000; C/Y = monthly = 12; Term = 5years
Step2: Calculate the total number of compoundings, n.
[latex]n=C/Y \times \text{(Number of Years)}=12 \times 5=60[/latex]
Step 3: Calculate the periodic rate, i.
[latex]\begin{align} FV&=PV(1+i)^n\\ \$21,\!799.42&=\$15,\!000(1+i)^{60}\\ 1.453294&=(1+i)^{60}\\ 1.453294^{\frac{1}{60}}&=1+i\\ 1.00625&=1+i\\ i&=0.00625 \end{align}[/latex]
Step 4: Calculate the nominal rate, I/Y.
[latex]\begin{align} i&=\frac{I/Y}{C/Y}\\ 0.00625&=\frac{I/Y}{12}\\ I/Y&=0.075\;\text{or}\;7.5\%\;\text{(compounded monthly)} \end{align}[/latex]
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 60 | Answer: 7.500003 | -15,000 | 0 | 21,799.42 | 12 | 12 |
Taryn’s investment in his RRSP earned 7.5% compounded monthly over the five years.
Converting Variable Interest Rates to a Fixed Interest Rate
When you deal with a series of variable interest rates it is extremely difficult to determine their overall effect. This also makes it hard to choose wisely between different series. For example, assume that you could place your money into an investment earning interest rates of 2%, 2.5%, 3%, 3.5%, and 4.5% over the course of five years, or alternatively you could invest in a plan earning 1%, 1.5%, 1.75%, 3.5%, and 7% (all rates compounded semi-annually). Which plan is better? The decision is unclear. But you can make it clear by converting the variable rates on each investment option into an equivalent fixed interest rate.
How It Works
Follow these steps to convert variable interest rates to their equivalent fixed interest rates:
Step 1: Draw a timeline for the variable interest rate. Identify key elements including any known PV or FV, interest rates, compounding, and terms.
Step 2: For each time segment, calculate the periodic interest rate (i) and the number of compoundings (n).
Step 3: One of three situations will occur, depending on what variables are known:
PV Is Known: Calculate the future value at the end of the transaction in each time segment, working left to right across the timeline.
FV Is Known: Calculate the present value at the beginning of the transaction in each time segment, working right to left across the timeline.
Neither PV nor FV Is Known: Pick an arbitrary number for PV ($10,000 is recommended) and solve for the future value in each time segment at the end of the transaction, working left to right across the timeline.
Step 4: Determine the compounding required on the fixed interest rate (C/Y) and calculate a new value for n to reflect the entire term of the transaction.
Step 5: Solve for i using the n from step 4 along with the starting PV and ending FV for the entire timeline.
Step 6: Solve for I/Y.
Example 9.5.3: Interest Rate under Variable Rate Conditions
Continue working with the two investment options mentioned previously. The choices are to place your money into a five year investment earning semi-annually compounded interest rates of either:
a) 2%, 2.5%, 3%, 3.5%, and 4.5%
b) 1%, 1.5%, 1.75%, 3.5%, and 7%
Calculate the equivalent semi-annual fixed interest rate for each plan and recommend an investment.
Solution:
Step 1: Draw a timeline for each investment option, as illustrated below.
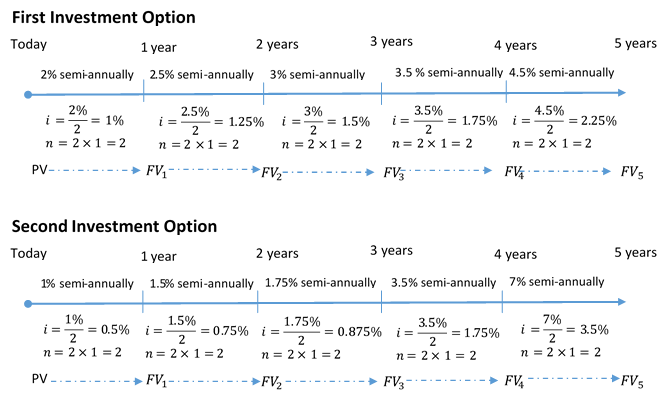
Step 2: For each time segment calculate i and n using the formulas[latex]i=\frac{I/Y}{C/Y}[/latex][latex]n=C/Y \times \text{Number of Years}[/latex]
Calculations are found in the timeline figure above.
Step 3: There is no value for PV or FV. Choose an arbitrary value of PV = $10,000 and solve for FV. Since only the interest rate fluctuates, solve in one calculation:
[latex]FV_5=PV \times (1+i_1)^{n_1} \times (1+i_2)^{n_2}\times \cdots \times (1+i_5)^{n_5}[/latex]
First Investment:
[latex]\small \begin{align} FV_5&=10,\!000(1+0.01)^{2} (1+0.0125)^{2}(1+0.015)^2(1+0.0175)^2(1+0.0225)^2\\ &=\$11,\!661.65972 \end{align}[/latex]
Second Investment:
[latex]\small \begin{align} FV_5&=10,\!000(1+0.005)^{2} (1+0.0075)^{2}(1+0.00875)^2(1+0.0175)^2(1+0.035)^2\\ &=\$11,\!570.14666 \end{align}[/latex]
Step 4:
First Investment: [latex]n=2 \times 5=10[/latex]
Second Investment: [latex]n=2 \times 5=10[/latex]
Step 5:
First Investment:
[latex]\begin{align} \$11,\!66165972&=\$10,\!000(1+i)^{10}\\ 1.166165&=(1+i)^{10}\\ 1.166165^{\frac{1}{10}}&=1+i\\ 1.001549&=1+i\\ i&=0.001549 \end{align}[/latex]
Second Investment:
[latex]\begin{align} \$11,\!570.14666&=\$10,\!000(1+i)^{10}\\ 1.157014&=(1+i)^{10}\\ 1.157015^{\frac{1}{10}}&=1+i\\ 1.014691&=1+i\\ i&=0.014691 \end{align}[/latex]
Step 6:
First Investment:
[latex]\begin{align} i&=\frac{I/Y}{C/Y}\\ 0.001549&=\frac{I/Y}{2}\\ I/Y&=0.030982\;\text{or}\;3.0982\% \end{align}[/latex]
Second Investment:
[latex]\begin{align} i&=\frac{I/Y}{C/Y}\\ 0.014691&=\frac{I/Y}{2}\\ I/Y&=0.029382\;\text{or}\;2.9382\% \end{align}[/latex]
First Investment:
| Time segment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | -10,000 | 0 | Answer: 10,201 | 2 | 2 |
| 2 | 2 | 2.5 | -10,201 | 0 | Answer: 10,457.61891 | 2 | 2 |
| 3 | 2 | 3 | -10,457.61891 | 0 | Answer: 10,773.70044 | 2 | 2 |
| 4 | 2 | 3.5 | -10,773.70044 | 0 | Answer: 11,154.0794 | 2 | 2 |
| 5 | 2 | 4.5 | -11,154.0794 | 0 | Answer: 11661.65972 | 2 | 2 |
| All | 2 | Answer: 0.030982 | -10000 | 0 | 11,661.66 | 2 | 2 |
Second Investment:
| Time segment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 60 | 1 | -10,000 | 0 | Answer: 10,100.25 | 2 | 2 |
| 2 | 60 | 1.5 | -10,100.25 | 0 | Answer: 10,252.32189 | 2 | 2 |
| 3 | 60 | 1.75 | -10,252.32189 | 0 | Answer: 10,432.52247 | 2 | 2 |
| 4 | 60 | 3.5 | -10,432.52247 | 0 | Answer: 10,800.85571 | 2 | 2 |
| 5 | 60 | 7 | -10,800.85571 | 0 | Answer: 11,570.14666 | 2 | 2 |
| All | 10 | Answer: 0.029382 | -10,000 | 0 | 11,570.15 | 2 | 2 |
The variable interest rates on the first investment option are equivalent to a fixed interest rate of 3.0982% compounded semi-annually. For the second option, the rates are equivalent to 2.9382% compounded semi-annually. Therefore, recommend the first investment since its rate is higher by 3.0982% − 2.9382% = 0.16% compounded semi-annually.
Exercises
In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.
- Your company paid an invoice five months late. If the original invoice was for $6,450 and the amount paid was $6,948.48, what monthly compounded interest rate is your supplier charging on late payments? (Answer: 18% compounded monthly)
- At what monthly compounded interest rate does it take five years for an investment to double? (Answer: 13.94% compounded monthly)
- Indiana just received a maturity value of $30,320.12 from a semi-annually compounded investment that paid 4%, 4.1%, 4.35%, 4.75%, and 5.5% in consecutive years. What amount of money did Indiana invest? What fixed quarterly compounded nominal interest rate is equivalent to the variable rate his investment earned? (Answer: $24,225 investment earned 4.51% compounded quarterly)
Image Descriptions
Figure 9.5.1: Timeline: PV = $7,100 at Today. FV = $8,615.19 at 3 years. Unknown % quarterly. [Back to Figure 9.5.1]
Figure 9.5.2: Timeline: PV = $15,100 at 5 years ago. FV = $15,000 +$6,799.42 = $21,799.42 at Today. Unknown % monthly. [Back to Figure 9.5.2]
Figure 9.5.3: First Investment Option Timeline: PV to 1 year as FV1 at 2% semi-annually with i=1% and n =2*1=2. FV1 to 2 years as FV2 at 2.5% semi-annually with i=1.25% and n =2*1=2. FV2 to 3 years as FV3 at 3% semi-annually with i=1.5% and n =2*1=2. FV3 to 4 years as FV4 at 3.5% semi-annually with i=1.75% and n =2*1=2. FV4 to 5 years as FV5 at 4.5% semi-annually with i=2.25% and n =2*1=2. Second Investment Option Timeline: PV to 1 year as FV1 at 1% semi-annually with i=0.5% and n =2*1=2. FV1 to 2 years as FV2 at 1.5% semi-annually with i=0.75% and n =2*1=2. FV2 to 3 years as FV3 at 1.75% semi-annually with i=0.875% and n =2*1=2. FV3 to 4 years as FV4 at 3.5% semi-annually with i=1.75% and n =2*1=2. FV4 to 5 years as FV5 at 7% semi-annually with i=3.5% and n =2*1=2. [Back to Figure 9.5.3]

