10.3: Application: Strip Bonds
Application: Strip Bonds
A strip bond is a marketable bond that has been stripped of all interest payments and is one of the many financial tools through which you may earn nontaxable income inside your Registered Retirement Savings Plan (RRSP). Mathematically, a strip bond essentially is a long-term version of the treasury bill. Whereas T-bills are found with terms of less than one year, strip bonds have longer terms because of the large sums of money that governments or large corporations require. These large sums take a long time to pay back.
How It Works
The future value of a strip bond is always known since it is the face value. You calculate the present value or purchase price by applying the following steps:
Step 1: Determine the face value (FV) of the strip bond, the years between the date of the sale and the maturity date (Years), the yield (I/Y) on the date of the sale, and the compounding frequency (C/Y). If needed, draw a timeline similar to the one below, which illustrates a typical strip bond timeline.
The compounding on strip bonds is assumed to be semi-annual unless stated otherwise. Thus, C/Y = 2 in most scenarios.

Step 2: Calculate the periodic interest rate (i) and the number of compounding periods (n) using the formulas
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compoundings per Year (C/Y)}}[/latex]
[latex]n=C/Y \times \text{(Number of Years)}[/latex]
Step 3: Calculate the present value (PV) of the strip bond using the formula
[latex]\begin{align}PV&=\frac{FV}{(1+i)^n}\end{align}[/latex]
Step 4: If you are interested in the actual dollar amount that the investor gains by holding onto the strip bond until maturity, use the formula for the amount of interest.
[latex]I=FV-PV[/latex]
Example 10.3.1: Purchase Price of a Strip Bond
Johansen is considering purchasing a $50,000 face value Government of Canada strip bond with 23½ years until maturity. The current market yield for these bonds is posted at 4.2031%. What is the price of the strip bond today, and how much money is gained if the bond is held until maturity?
Solution:
Step 1: The timeline below illustrates the scenario.

Step 2: Calculate the periodic interest rate (i) and the number of compounding periods (n).
[latex]i=\frac{I/Y}{C/Y}=\frac{4.2031\%}{2}=2.10155\%\;\text{or}\;0.0210155[/latex]
[latex]n=C/Y \times \text{(Number of Years)}=2 \times 23.5=47[/latex]
Step 3: Calculate the present value, PV.
[latex]\begin{align} PV&=\frac{FV}{(1+i)^n}\\ &=\frac{\$50,\!000}{(1+0.0210155)^{47}}\\ &=\$18,\!812.66 \end{align}[/latex]
Step 4: Calculate the amount of interest.
[latex]I=FV-PV=\$50,\!000-\$18,\!812.66=\$31,\!187.34[/latex]
Calculator instructions:
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 47 | 4.2031 | Answer: -18,812.66199 | 0 | 50,000 | 2 | 2 |
The strip bond has a purchase price of $18,812.66 today. If you hold onto the strip bond until maturity, you will receive a payment of $50,000 23½ years from today. This represents a $31,187.34 gain.
Nominal Yields on Strip Bonds
To calculate nominal yields you need the same four formulas as for the strip bond’s purchase price.
How It Works
Follow these steps to calculate the nominal yield of a strip bond:
Step 1: Determine the present value or purchase price of the strip bond (PV). This may already be known, or you may have to calculate this amount using the previously introduced steps for calculating the present value.
Step 2: Determine the future value (FV) of the strip bond. If it is the maturity of the strip bond, then the future value is the face value of the bond. If the investor is selling the strip bond prior to maturity, then this number is based on a present value calculation using the yield at the time of sale and time remaining until maturity.
Step 3: Determine the years between the purchase and the sale of the strip bond.
Using C/Y = 2 (unless otherwise stated), calculate the number of compounding periods (n) using the formula
[latex]n=C/Y \times \text{(Number of Years)}[/latex]
Step 4: Calculate the periodic interest rate (i). Use Formula 9.2B, rearrange and solve for i.
Step 5: Calculate the nominal interest rate (I/Y).
Use Formula 9.1, rearrange and solve for I/Y.
Step 6: If you are interested in the actual dollar amount that the investor gained while holding the strip bond, use the formula for the amount of interest.
[latex]I=FV-PV[/latex]
Example 10.3.2: The Investor’s Actual Yield (PV known)
Assume that when market yields were 4.254% an investor purchased a $25,000 strip bond 20 years before maturity. The purchase price was $10,772.52. The investor then sold the bond five years later, when current yields dropped to 3.195%. The selling price was $15,539.94. The investor wants to know the gain and the actual yield realized on her investment.
Solution:
Step 1: PV = $10,772.52. This is the purchase price paid for the strip bond.
Step 2: FV = $15,539.94. This is the selling price received for the strip bond.
Step 3: C/Y = 2; Years = 5 (between the purchase and sale price);
[latex]n=C/Y \times \text{(Number of Years)}=2 \times 5=10[/latex]
Step 4: Calculate the periodic interest rate, i.
[latex]\begin{align} FV&=PV(1+i)^n\\ \$15,\!539.94&=\$10,\!772.52(1+i)^{10}\\ 1.442554&=(1+i){10}\\ 1.442554^{\frac{1}{10}}&=1+i\\ 1.037321&=1+i\\ i&=0.037321 \end{align}[/latex]
Step 5: Calculate the nominal interest rate, I/Y.
[latex]i=\frac{I/Y}{C/Y}[/latex]
[latex]\begin{align} I/Y&=i \times C/Y\\ &=0.037321 \times 2\\ &=0.074642\%\; \text{or}\; 7.4642\% \end{align}[/latex]
Step 6: Calculate the actual gain (interest earned).
[latex]I=FV-PV=\$15,\!539.94-\$10,\!772.52=$4,\!767.42[/latex]
The investor gained $4,767.42 on the investment, representing an actual yield of 7.4642% compounded semiannually.
Concept Check:
Example 10.3.3: The Investor’s Actual Yield (PV unknown)
Cameron invested in a $97,450 face value Government of British Columbia strip bond with 25 years until maturity. Market yields at that time were 9.1162%. Ten and half years later Cameron needed the money, so he sold the bond when current yields were 10.0758%. Calculate the actual yield and gain that Cameron realized on his investment.
Solution:
The timeline below illustrates the situation.
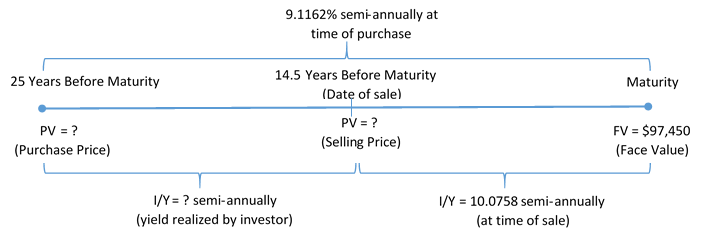
Step 1: Calculate the purchase price (PV) based on the purchase date.
I/Y = 9.1162%; C/Y = 2; Years = 25
[latex]i=\frac{I/Y}{C/Y}=\frac{9.1162\%}{2}=4.5581\%[/latex]
[latex]n=C/Y \times \text{(Number of Years)}=2 \times 25=50[/latex]
[latex]\begin{align} PV&=\frac{\$97,\!450}{(1+0.045581)^{50}}\\ &=\$10,\!492.95 \end{align}[/latex]
Step 2: Calculate the selling price (PV) based on the selling date.
I/Y = 10.0758%; C/Y = 2; Years = 14.5
[latex]i=\frac{I/Y}{C/Y}=\frac{10.0758\%}{2}=5.0379\%[/latex]
[latex]n=C/Y \times \text{(Number of Years)}=2 \times 14.5=29[/latex]
[latex]\begin{align} PV&=\frac{\$97,\!450}{(1+0.050379)^{29}}\\ &=\$23,\!428.63 \end{align}[/latex]
This becomes the FV for subsequent calculations.
Step 3: C/Y = 2; Years = 14.5
[latex]n=C/Y \times \text{(Number of Years)}=2 \times 10.5=21[/latex]
Step 4: Calculate the periodic interest rate, i.
PV=$10,492.95; FV=$23,428.63
[latex]\begin{align} FV&=PV(1+i)^n\\ \$23,\!428.63&=\$10,\!492.95(1+i)^{21}\\ 2.232797&=(1+i){21}\\ 2.232797^{\frac{1}{21}}&=1+i\\ 1.038991&=1+i\\ i&=0.038991 \end{align}[/latex]
Step 5: Calculate the nominal interest rate, I/Y.
[latex]\begin{align} I/Y&=i \times C/Y\\ &=0.038991 \times 2\\ &=0.077982\%\; \text{or}\; 7.7982\% \end{align}[/latex]
Step 6: Calculate the actual gain (interest earned).
[latex]I=FV-PV=\$23,\!428.63-\$10,\!492.95=\$12,\!935.68[/latex]
Calculator instructions:
|
Step |
N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 50 | 9.1162 | Answer: -10,492.95246 | 0 | 97,450 | 2 | 2 |
| 2 | 29 | 10.0758 | Answer: -23,428.63365 | 0 | 97,450 | 2 | 2 |
| 4 and 5 | 21 | Answer: 7.798240 | -10,492.95 | 0 | 23,428.63 | 2 | 2 |
Cameron sold the strip bond when prevailing market rates were higher than the rate at the time of purchase. He has realized a lower yield of 7.7982% compounded semi-annually, which is a gain of $12,935.68.
Exercises
In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.
- A $15,000 face value Government of Manitoba strip bond has 19.5 years left until maturity. If the current market rate is posted at 6.7322% compounded semi-annually, what is the purchase price for the bond? (Answer: $4,124.24)
- An investor purchased a $7,500 face value strip bond for $2,686.01 on May 29, 2006. The strip bond had been issued on May 29, 2002, with a 25-year maturity. The investor sold the strip bond on November 29, 2012, for $3,925.28.
a) What was the market yield when the investor purchased the strip bond? (Answer: 4.95% compounded semi-annually)
b) What was the market yield when the investor sold the strip bond? (Answer: 4.5155% compounded semi-annually)
c) What actual yield did the investor realize on the strip bond? (Answer: 5.9226% compounded semi-annually)
Timelines for the exercises are included in Solution to Exercises.
Image Descriptions
Figure 10.3.0: Timeline showing PV = ? (Amount to Invest) at Today. FV = Face Value of Strip Bond at Maturity Date of Strip Bond. Unknown % semi-annually. Arrow from the right (Maturity Date of the Strip Bond) back to the left (Today). [Back to Fgure 10.3.0]
Figure 10.3.1: Timeline showing PV = ? at Today. FV = $50,000 (Face Value) at 23.5 years. 4.2031% semi-annually. Arrow from 23.5 years back to the left (Today). [Back to Fgure 10.3.1]
Figure 10.3.3: Timeline showing PV = ? (Purchase Price) at 25 Years Before Maturity. PV = ? (Selling Price) at 14.5 Years Before Maturity (Date of Sale). FV = $97,450 (Face Value) at Maturity. 9.11652% semi-annually at time of purchase (25 years before maturity to maturity). I/Y = ? semi-annually (yield realized by investor) from 25 years before maturity to 14.5 years before maturity. I/Y = 10.0758% semi-annually (at time of sale) from 14.5 years before maturity to maturity. [Back to Fgure 10.3.3]

