12.1: Deferred Annuities
Deferred Annuities
What is a Deferred Annuity?
A deferred annuity is a financial transaction where annuity payments are delayed until a certain period of time has elapsed. Usually the annuity has two stages, as depicted in this figure.
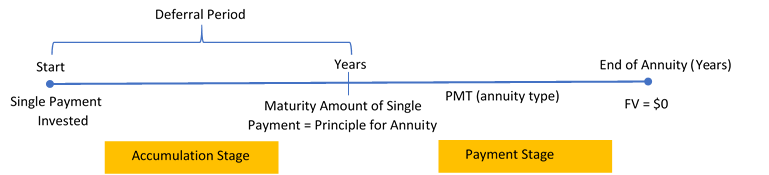
- Accumulation Stage. A single payment is allowed to earn interest for a specified duration. There are no annuity payments during this period of time, which is commonly referred to as the period of deferral.
- Payments Stage. The annuity takes the form of any of the four annuity types and starts at the beginning of this stage as per the financial contract. Note that the maturity value of the accumulation stage is the same as the principal for the payments stage.
The interest rate on deferred annuities can be either variable or fixed. However, since deferred annuities are commonly used to meet a specific need, fixed interest rates are more prevalent since they allow for certainty in the calculations.
The Formula
For a deferred annuity, you apply a combination of formulas that you have already used throughout this book. The accumulation stage is not an annuity, so it uses the various single payment compound interest formulas from Chapter 9. The payments stage is an annuity, so it uses the various annuity formulas from Chapter 11.
How It Works
For deferred annuities, the most common unknown variables are either the present value, the length of the period of deferral, the annuity payment amount, or the number of annuity payments that are sustainable for a fixed income payment. Follow this sequence of steps for each of these variables:
| Solving for the Present Value | Solving for the Period of Deferral | Solving for the Annuity Payment Amount | Solving for the Number of Annuity Payments |
|---|---|---|---|
| Step 1: Draw a timeline and identify the variables that you know, along with the annuity type. | Step 1: Draw a timeline and identify the variables that you know, along with the annuity type. | Step 1: Draw a timeline and identify the variables that you know, along with the annuity type. | Step 1: Draw a timeline and identify the variables that you know, along with the annuity type. |
| Step 2: Starting at the end of your timeline, calculate the present value of the annuity using the steps from Section 11.3 (Formulas 11.4 or 11.5). Round your answer to two decimals. | Step 2: Starting at the end of your timeline, calculate the present value of the annuity using the steps from Section 11.3 (Formulas 11.4 or 11.5). Round your answer to two decimals. | Step 2: Starting at the beginning of the timeline, calculate the future value of the single payment using the steps from Section 9.2 (Formula 9.3). Round your answer to two decimals. | Step 2: Starting at the beginning of the timeline, calculate the future value of the single payment using the steps from Section 9.2 (Formula 9.3). Round your answer to two decimals. |
| Step 3: Take the principal of the annuity, and using the steps from Section 9.3 (Formula 9.3) calculate the present value for the single amount. | Step 3: Solve for the number of compounding periods using the applicable steps from Section 9.7 (Formula 9.3). The single payment investment is the present value, and the principal of the annuity is the future value. | Step 3: Calculate the annuity payment amount using steps from Section 11.4 (Formula 11.4 or 11.5). | Step 3: Calculate the number of annuity payments using steps from Section 11.5 (Formula 11.4 or 11.5). |
Important Notes
Rounding
The maturity value of the single payment or the present value of the annuity is always rounded to two decimals. Since an accumulation fund is different from a payment annuity, logistically the money is transferred between different bank accounts, which means that only two decimals are carried either forwards or backwards through this step of the required calculations.
Combining the Deferral Period and the Annuity Term.
It is an error to treat the period of deferral and the term of the annuity as simultaneous time periods. For example, if a deferred annuity has a three-year period of deferral and a 10-year annuity term, this is sometimes interpreted, mistakenly, as an annuity ending 10 years from today. These time segments are separate and consecutive on the timeline! The correct interpretation is that the annuity term ends 13 years from today, since the 10-year term does not start until the three-year deferral terminates.
Incorrect Timing between Stages
A common mistake is to determine incorrectly when the period of deferral ends and the annuity starts. This error usually results from forgetting that the payments on ordinary annuities start one payment interval after the annuity starts, whereas annuity due payments start immediately. Thus, if the first quarterly payment on an ordinary annuity is to be paid 6¾ years from today, then the period of deferral is 6½ years. If the deferral is for an annuity due, then the period of deferral is 6¾ years.
Confusing n
A deferred annuity requires different calculations of n using either Formula 9.2A or Formula 11.1.
In the accumulation stage, recall that n must represent the number of compound periods calculated by Formula 9.2A.
In the payments stage, the n must represent the number of annuity payments calculated by Formula 11.1.
Concept Check
Example 12.1.1: Investing an Inheritance for Your Retirement
Frasier is 33 years old and just received an inheritance from his parents’ estate. He wants to invest an amount of money today such that he can receive $5,000 at the end of every month for 15 years when he retires at age 65. If he can earn 9% compounded annually until age 65 and then 5% compounded annually when the fund is paying out, how much money must he invest today?
Solution:
Calculate the single payment that must be invested today. This is the present value (PV) of the deferred annuity.
Step 1: The deferred annuity has monthly payments at the end with an annual interest rate. Therefore, this is an ordinary general annuity.
The timeline for the deferred annuity appears below.
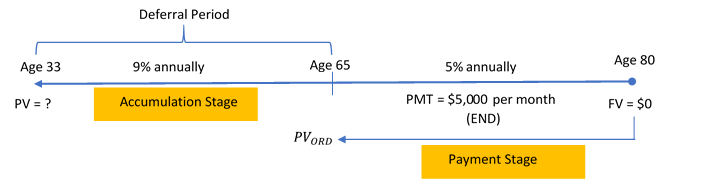
Ordinary General Annuity (Payment Stage):
FV = $0; I/Y = 5%; C/Y = 1; PMT = $5,000; P/Y = 12; Years = 15
Period of Deferral (Accumulation Stage):
FV = PVORD; I/Y = 9%; C/Y = 1; Years = 32
Step 2: Ordinary General Annuity (Payment Stage):
Calculate the equivalent periodic interest rate that matches the payment interval (ieq, Formula 9.6), number of annuity payments (n, Formula 11.1), and present value of the ordinary general annuity (PVORD, Formula 11.3A).
[latex]i=\frac{I/Y}{C/Y}=\frac{5\%}{1}=5\%[/latex]
[latex]i_{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.05)^{\frac{1}{12}}-1=0.004074124\;\text{per month}[/latex]
[latex]n=P/Y \times \text{(Number of Years)}=12 \times 15=180\;\text{payments}[/latex]
[latex]\begin{align} PV_{ORD}&=PMT \left[\frac{1-(1+i)^{-n}}{i}\right]\\ &=\$5,\!000\left[\frac{1-(1+0.004074124)^{-180}}{0.004074124}\right]\\ &=\$5,\!000\left[\frac{0.518982921}{0.004074124}\right]\\ &=\$636,\!925.79 \end{align}[/latex]
Step 3: Deferral Period (Accumulation Stage):
Discount the principal of the annuity (PVORD) back to today (Age 33). Calculate the periodic interest rate (i, Formula 9.1), number of single payment compound periods (n, Formula 9.2A), and present value of a single payment (PV, Formula 9.2B), rearranged.
[latex]i=\frac{I/Y}{C/Y}={9\%}{1}=9\%[/latex]
[latex]n=C/Y \times \text{(Number of Years)}=1 \times 32=32\;\text{compounds}[/latex]
[latex]\begin{align} PV&=\frac{FV}{(1+i)^n}\\ &=\frac{\$636,\!925.79}{(1+0.09)^{32}}\\ &=\$40,\!405.54 \end{align}[/latex]
Calculator instructions:
| Stage | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| Payments | END | 180 | 5 | Answer: -636,925.79 | 5,000 | 0 | 12 | 1 |
| Accumulation | END | 32 | 9 | Answer: 40,405.53861 | 0 | 636,925.79 | 1 | 1 |
If Frasier invests $40,405.54 today, he will have enough money to sustain 180 withdrawals of $5,000 in retirement.
Example 12.1.2: Planning the Deferral Period
Bashir wants an annuity earning 4.3% compounded semi-annually to pay him $2,500 at the beginning of every month for 10 years. To achieve his goal, how far in advance of the start of the annuity does Bashir need to invest $50,000 at 8.25% compounded quarterly? Assume 91 days in a quarter.
Solution:
Calculate the amount of time between today and the start of the annuity. This is the period of deferral, or n.
Step 1: The deferred annuity has monthly payments at the beginning with a semi-annual interest rate. Therefore, this is a general annuity due.
The timeline for the deferred annuity appears below.
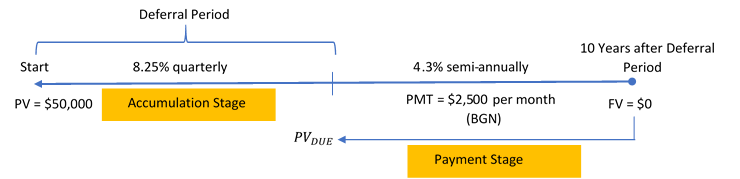
Ordinary General Annuity (Payment Stage):
FV = $0; I/Y = 4.3%; C/Y = 2; PMT = $2,500; P/Y = 12; Years = 10
Period of Deferral (Accumulation Stage):
PV = $50,000; FV = PVDUE; I/Y = 8.25%, C/Y = 4
Step 2: Ordinary General Annuity (Payment stage):
Calculate the equivalent periodic interest rate that matches the payment interval (ieq, Formula 9.6), number of annuity payments (n, Formula 11.1), and present value of the annuity due (PVDUE, Formula 11.3B).
[latex]i=\frac{I/Y}{C/Y}=\frac{4.3\%}{2}=2.15\%[/latex]
[latex]i_{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.0205)^{\frac{2}{12}}-1=0.003551648\;\text{per month}[/latex]
[latex]n=P/Y \times \text{(Number of Years)}=12 \times 10=120\;\text{payments}[/latex]
[latex]\begin{align} PV_{DUE}&=PMT \left[\frac{1-(1+i_{eq})^{-n}}{i_{eq}}\right] \times(1+i_{eq})\\ &=\$2,\!500 \left[\frac{1-(1+0.003551648)^{-120}}{0.003551648}\right] \times(1+0.003551648)\\ &=\$244,\!780.93 \end{align}[/latex]
This becomes FV for the deferral period in step 3.
Step 3: Deferral Period (Accumulation stage):
[latex]i=\frac{I/Y}{C/Y}=\frac{8.25\%}{4}=2.0625\%[/latex]
[latex]\begin{align} FV&=PV(1+i)^n\\ \$244,\!780.93&=\$50,\!000(1+0.020625)^n\\ 4.895618&=1.020625^n\\ \ln(4.85618)&=n \times \ln(1.020625)\\ n&=\frac{1.588340}{0.020415}\\ &=77.801923\;\text{quarterly compounds} \end{align}[/latex]
Convert n to years, months and days.
[latex]\begin{align} \text{Years}&=\frac{77}{4}\\ &=19.25= 19\; \text{years,}\; 3\; \text{months}\\ \end{align}[/latex]
[latex]0.801923 \times 91 \;\text{days}=72.975105=73\;\text{days}[/latex]
19 years, 3 months, 73 days
Calculator instructions:
| Stage | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| Payments | BGN | 120 | 4.3 | Answer: -244,780.9336 |
2,500 | 0 | 12 | 2 |
| Accumulation | END | Answer: 77.801924 | 8.25 | -5,000 | 0 | 244,780.93 | 4 | 4 |
To achieve his goal, Bashir needs to invest the $50,000 19 years, 3 months and 73 days before the annuity starts.
Example: 12.1.3: How Much Income will It Provide
On the day of their granddaughter’s birth, Henri and Frances deposited $3,000 into a trust fund for her future education. The fund earns 6% compounded monthly. When she turns 18, they then want it to make payments at the end of every quarter for five years. If the income annuity can earn 4.5% compounded quarterly, what is the amount of each annuity payment to the granddaughter?
Solutions:
Step 1: The deferred annuity has quarterly payments at the end with a quarterly interest rate. Therefore, this is an ordinary simple annuity.
The timeline for the deferred annuity appears below.

Period of Deferral (Accumulation Stage):
PV = $3,000; I/Y = 6%, C/Y = 12; Years = 18
Ordinary Simple Annuity (Payment Stage):
PVORD = FV (after deferral); FV = $0; I/Y = 4.5%; C/Y = 4; P/Y = 4; Years = 5
Step 2: Calculate the future value of the single payment investment. Calculate the periodic interest rate (i, Formula 9.1), number of single payment compound periods (n, Formula 9.2A), and future value of a single payment amount (FV, Formula 9.2B).
[latex]i=\frac{I/Y}{C/Y}=\frac{6\%}{12}=0.5\%[/latex]
[latex]n=C/Y \times \text{(Number of Years)}=12 \times 18=216\;\text{compounds}[/latex]
[latex]\begin{align} FV&=PV(1+i)^n\\ &=\$3,\!000(1+0.005)^{216}\\ &=\$8,\!810.30 \end{align}[/latex]
Step 3: Work with the ordinary simple annuity. First, calculate the periodic interest rate (i, Formula 9.1), number of annuity payments (n, Formula 11.1), and finally the annuity payment amount (PMT, Formula 11.3A).
[latex]i=\frac{I/Y}{C/Y}=\frac{4.5\%}{4}=1.125\%[/latex]
[latex]n=P/Y \times \text{(Number of Years)}=4 \times 5=20\;\text{payments}[/latex]
[latex]\begin{align} PV_{ORD}&=PMT \left[\frac{1-(1+i)^{-n}}{i}\right]\\ \$8,\!810.30&=PMT\left[\frac{1-(1+0.01125)^{-20}}{0.01125}\right]\\ \$8,\!810.30&=PMT\left[\frac{0.200480}{0.01125}\right]\\ \$8,\!810.30&=PMT (17.820448)\\ PMT&=\frac{\$8,\!810.30}{17.820448}\\ &=\$494.39 \end{align}[/latex]
Calculator instructions:
| Stage | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| Payments | END | 216 | 6 | -3,000 | 0 | Answer: 8,810.297916 | 12 | 12 |
| Accumulation | END | 20 | 4.5 | -8,810.30 | Answer: 494.392721 | 0 | 4 | 4 |
The granddaughter will receive $494.39 at the end of every quarter for five years starting when she turns 18. Since the payment is rounded, the very last payment is a slightly different amount, which could be determined exactly using techniques discussed in Chapter 13.
Example 12.1.4: How Long Can the Annuity be Sustained
Emile received a $25,000 one-time bonus from his employer today, and he immediately invested it at 8% compounded annually. Fourteen years from now, he plans to withdraw $2,300 at the beginning of every month to use as his retirement income. If the income annuity can earn 3.25% compounded semi-annually, what is the term of the annuity before it is depleted (including the smaller final payment)?
Solution:
Figure out how long the income annuity is able to sustain the income payments. This requires you to calculate the number of annuity payments, or n.
Step 1: The deferred annuity has monthly payments at the beginning with a semi-annual interest rate. Therefore, this is a general annuity due.
The timeline for the deferred annuity appears below.
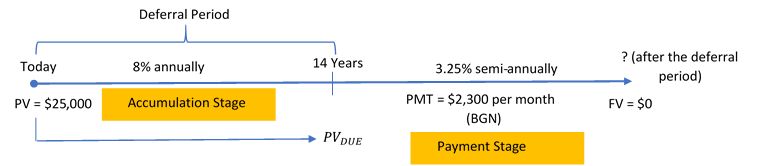
Period of Deferral (Accumulation Stage):
PV = $25,000; I/Y = 8%, C/Y = 1; Years = 14
General Annuity Due (Payment Stage):
PVDUE = FV (after deferral); FV = $0; I/Y = 3.25%; C/Y = 2; PMT = $2,300; P/Y = 12
Step 2: Calculate the future value of the single deposit. Calculate the periodic interest rate (i, Formula 9.1), number of single payment compound periods (n, Formula 9.2A), and future value of a single payment amount (FV, Formula 9.2B).
[latex]i=\frac{I/Y}{C/Y}=\frac{8\%}{1}=8\%[/latex]
[latex]n=C/Y \times \text{(Number of Years)}=1 \times 14=14\;\text{compounds}[/latex]
[latex]\begin{align} FV&=PV(1+i)^n\\ &=\$25,\!000(1+0.08)^{14}\\ &=\$73,\!429.84 \end{align}[/latex]
Step 3: Work with the general annuity due. Calculate the equivalent periodic interest rate (ieq, Formula 9.6) that matches the payment interval and the number of annuity payments (n, Formula 11.3B rearranged for n). Finally substitute into the annuity payments Formula 11.1 to solve for Years.
[latex]i=\frac{I/Y}{C/Y}=\frac{3.25\%}{2}=1.625\%[/latex]
[latex]i_{eq}=(1+i)^{\frac{C/Y}{P/Y}}-1=(1+0.01625)^{\frac{2}{12}}-1=0.002690\;\text{per month}[/latex]
[latex]\begin{align} PV_{DUE}&=PMT \left[\frac{1-(1+i_{eq})^{-n}}{i_{eq}}\right] \times(1+i_{eq})\\ 73,\!429.84&=\$2,\!300 \left[\frac{1-(1+0.002690)^{-n}}{0.002690}\right] \times(1+0.002690)\\ 31.840361&=\frac{1-0.997317^n}{0.002690}\\ 0.085656&=1-0.99730\\ \ln(0.997317)&=n \times \ln(0.914343)\\ n&=33.332019 =34\;\text{payments} \end{align}[/latex]
[latex]\begin{align} \text{Years}&=\frac{34}{12}\\ &=2.8\overline{3}\\ &= 2\;\text{years and}\; 0.8\overline{3}\times 12=10\;\text{months} \end{align}[/latex]
Calculator Instructions:
| Stage | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| Payments | END | 14 | 8 | -25,000 | 0 | Answer: 73,429.84061 |
1 | 1 |
| Accumulation | BGN | Answer: 33.332019 | 3.25 | -73,429.84 | 2,300 | 0 | 12 | 2 |
The annuity will last 2 years and 10 months before being depleted.
Exercises
In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.
- What is the present value of a deferred annuity with a deferral period of 17 years at 6.7% compounded semi-annually followed by a 10-year annuity due paying $1,250 at the beginning of every month at 4.78% compounded semi-annually? (Answer: $439,070.09)
- Your objective is an annuity due paying $5,000 semi-annually for 5.5 years at 4% compounded quarterly. How far in advance of this would you need to invest $20,000 at 6.82% compounded monthly? Express answer in years and months. (Answer: 13 years, 6 months)
- Jeff and Sarah want an ordinary annuity to pay their daughter $1,000 monthly for three years and nine months for the duration of her educational studies starting August 1, 2024. What lump-sum amount do they need to invest on August 1, 2014, if the deferred annuity can earn 6.6% compounded monthly during the accumulation stage and 4% compounded quarterly during the income payments stage? (Answer: $21,609.06)
- At the age of 44, Parker just finished all the arrangements on his parents’ estate. He is going to invest his $80,000 inheritance at 5.5% compounded quarterly until he retires at age 55, and then wants to receive month-end payments for the next 25 years. The income annuity is expected to earn 3.85% compounded annually. What are his monthly annuity payments during his retirement? (Answer: $752.78)
- Once Jason graduated college at age 22, he invested $350 into his RRSP at the beginning of every month until age 40. He then stopped his contributions and let the amount earn interest until today, when at age 62 he decided to retire. He wants his retirement money to last until age 85. If his account can earn 10.4% compounded quarterly before age 62 and 4.8% compounded annually after that, how much money can he expect to receive at the end of every quarter? (Answer: $37,571.53)
Timelines for the exercises are included in Solutions to Exercises
Image Descriptions
Figure 12.1.0: Timeline showing a Single Payment Invested at Start and a Deferral Period (Accummulation Stage) from Start to Years. At Years, Maturity Amount of Single Payment = Principal of Annuity. From Years to End of Annuity (Years), Payment Stage with PMT (annuity type). At End of Annuity (Years), FV = $0 [Back to Figure 12.1.0]
Figure 12.1.1: Timeline showing at Age 80, FV = $0. From Age 80, FV is brought back to Age 65 as PVord. From Age 80 to Age 65 (Payment Stage), 5% annually and PMT = $5,000 per month (END). Deferral Period (Accummulation Stage) from Age 33 to Age 65 with 9% annually. [Back to Figure 12.1.1]
Figure 12.1.2: Timeline showing at 10 Years after Deferral Period, FV = $0. From 10 Years after Deferral Period, FV is brought back to end of Deferral Period as PVdue. From 10 Years after Deferral Period to End of Deferral Period (Payment Stage), 4.3% semi-annually and PMT = $2,500 per month (BGN). Deferral Period (Accummulation Stage) from Start to End of Deferral Period with 8.25% quarterly. At Start, PV = $50,000. [Back to Figure 12.1.2]
Figure 12.2.3: Timeline: At Birth, PV = $3,000. From Birth to Age 18 (Deferral Period =Accumulation Stage) with 6% monthly. PV at Birth moves to Age 18 as PVord = FV (after deferral). From Age 18 to Age 23 is the Payment Stage with 4.5% quaterly and PMT = ? per quarter (END). At Age 23, FV = $0. [Back to Figure 12.1.3]
Figure 12.1.4: Timeline: Today, PV = $25,000. From Today to 14 years (Deferral Period =Accumulation Stage) with 8% annually. PV at today moves to 14 Years as PVdue= FV (after deferral). From 14 Years to is the Payment Stage with 3.25% semi-annually and PMT = 2,3000 per month (BGN). At ? (after the deferral period), FV = $0. [Back to Figure 12.1.4]

