Chapter 12: Solution to Exercises

12.1: Deferred Annuities

1. What is the present value of a deferred annuity with a deferral period of 17 years at 6.7% compounded semi-annually followed by a 10-year annuity due paying $1,250 at the beginning of every month at 4.78% compounded semi-annually?

Solution:

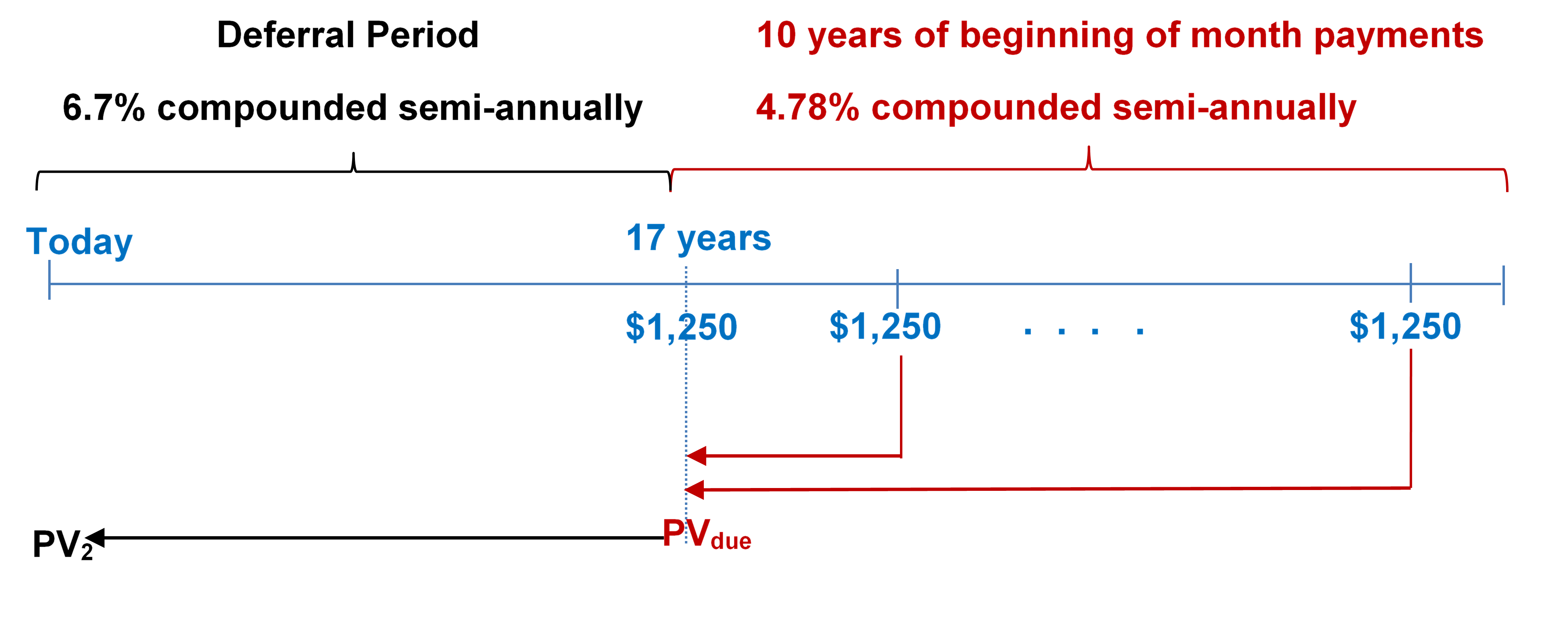
Step 1: Find [latex]PV_{due}[/latex].

Mode = BGN

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 10 \times 12 = 120 \;\text{payments}[/latex]
[latex]I/Y = 4.78[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]FV = 0[/latex]
[latex]PMT = 1,\!250[/latex]
[latex]CPT\; PV_{due} = -\$119,\!784.53\;\text{(This becomes +FV for Step 2)}[/latex]

Step 2: Find [latex]PV_{2}[/latex].

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 17 \times 2 = 34 \;\text{payments}[/latex]
[latex]I/Y = 6.7[/latex]
[latex]P/Y = 2[/latex]
[latex]C/Y = 2[/latex]
[latex]PMT = 0[/latex]
[latex]FV = 119,\!784.53[/latex]
[latex]PMT = 0[/latex]
[latex]CPT\; PV_{2} = - \$39,\!070.09[/latex]

The present value is $39,070.09.

2. Your objective is an annuity due paying $5,000 semi-annually for 5.5 years at 4% compounded quarterly. How far in advance of this would you need to invest $20,000 at 6.82% compounded monthly? Express answer in years and months.

Solution:

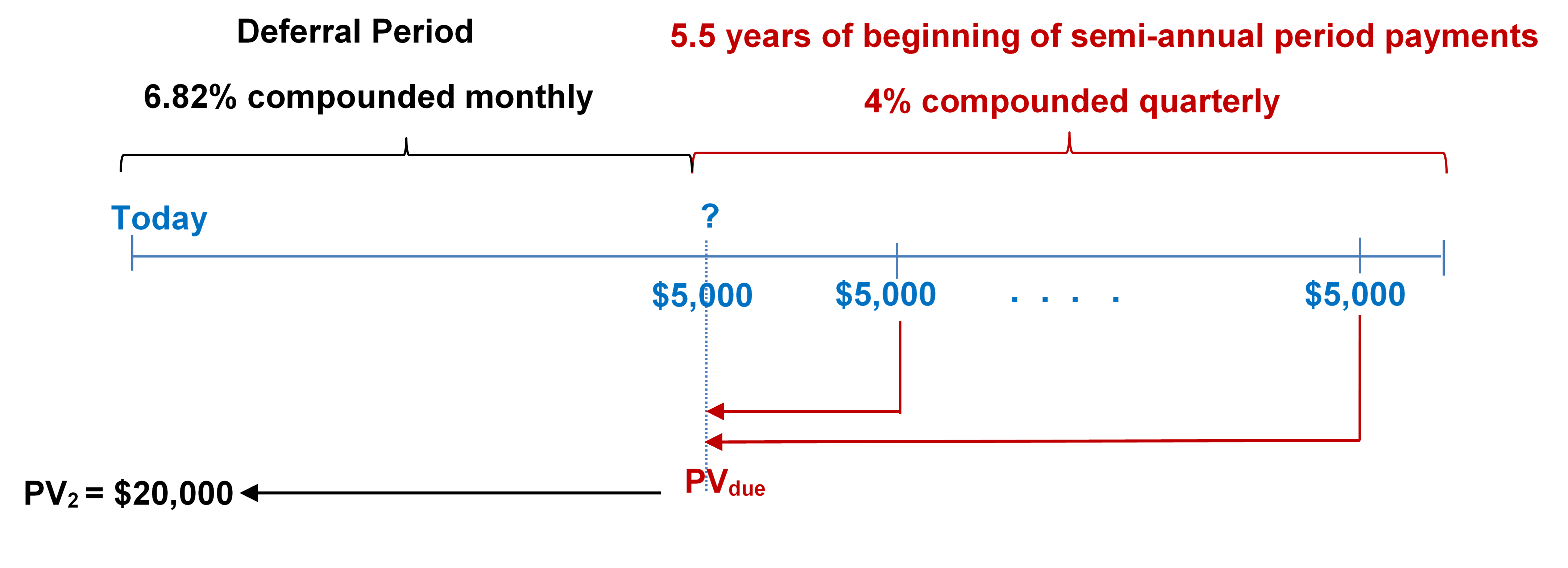
Step 1: Find [latex]PV_{due}[/latex].

Mode = BGN

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 5.5 \times 2 = 11 \;\text{payments}[/latex]
[latex]I/Y = 4[/latex]
[latex]P/Y = 2[/latex]
[latex]C/Y = 4[/latex]
[latex]PMT = 5,\!000[/latex]
[latex]FV = 0[/latex]
[latex]CPT\; PV_{due} = -\$49,\!889.44\;\text{(This becomes +FV for Step 2)}[/latex]

Step 2: Find [latex]N[/latex].

Mode = END

[latex]I/Y = 6.82[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 12[/latex]
[latex]PMT = 0[/latex]
[latex]FV = 49,\!889.44[/latex]
[latex]PV_{2} =-20,\!000[/latex]
[latex]CPT\; N = 161.291284 \;\text{rounded up to}\;162\; \text{monthly payments}[/latex]

[latex]\begin{align} {\text{Number of years}}&=\frac{162}{12}\\ &= 13.5 \end{align}[/latex]

13 years, 6 months

3. Jeff and Sarah want an ordinary annuity to pay their daughter $1,000 monthly for three years and nine months for the duration of her educational studies starting August 1, 2024. What lump-sum amount do they need to invest on August 1, 2014, if the deferred annuity can earn 6.6% compounded monthly during the accumulation stage and 4% compounded quarterly during the income payments stage?

Solution:

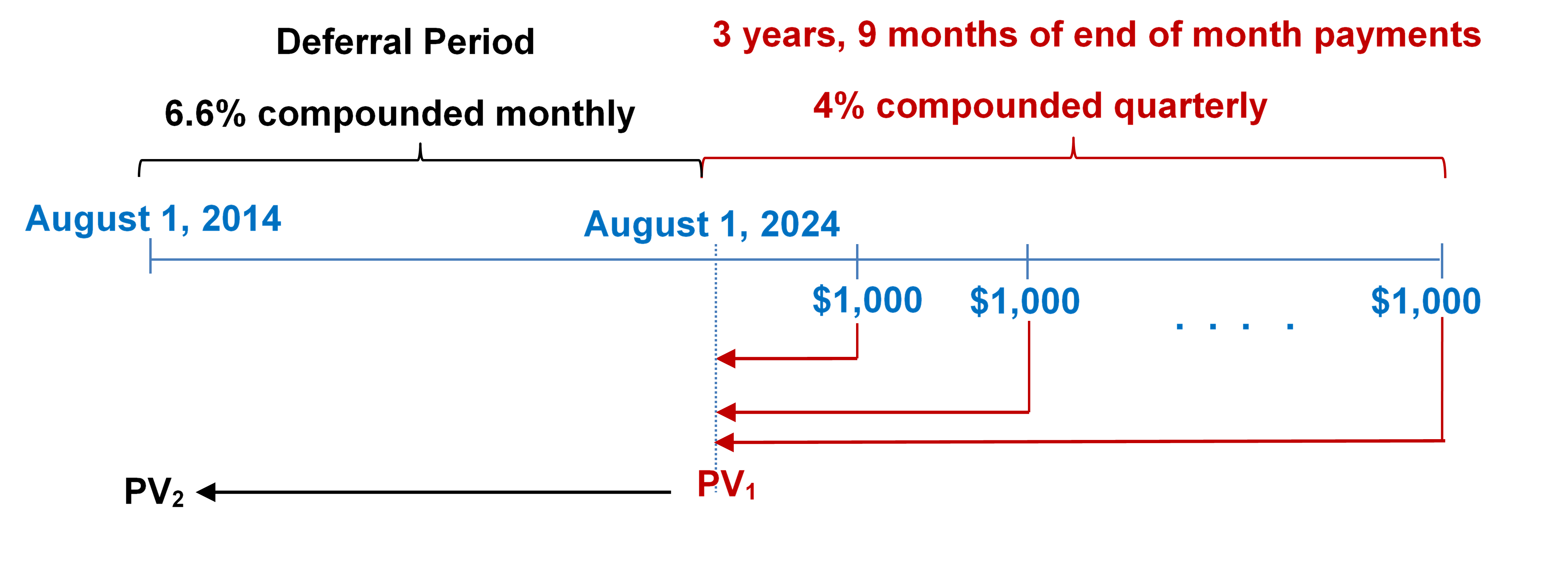
Step 1: Find [latex]PV_1[/latex].

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 3.5 \times 12 = 45 \;\text{payments}[/latex]
[latex]I/Y = 4[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 4[/latex]
[latex]PMT = 1,\!000[/latex]
[latex]FV = 0[/latex]
[latex]CPT\; PV_1 = -\$41,\!733.50\;\text{(This becomes +FV for Step 2)}[/latex]

Step 2: Find [latex]PV_2[/latex].

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 10 \times 12 = 120 \;\text{payments}[/latex]
[latex]I/Y = 6.6[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 12[/latex]
[latex]PMT = 0[/latex]
[latex]FV =\$41,\!733.50[/latex]
[latex]CPT\; PV_2 = - \$21,\!609.06[/latex]

They need to invest $21,609.06 on August 1, 2014.

4. At the age of 44, Parker just finished all the arrangements on his parents’ estate. He is going to invest his $80,000 inheritance at 5.5% compounded quarterly until he retires at age 55, and then wants to receive month-end payments for the next 25 years. The income annuity is expected to earn 3.85% compounded annually. What are his monthly annuity payments during his retirement?

Solution:

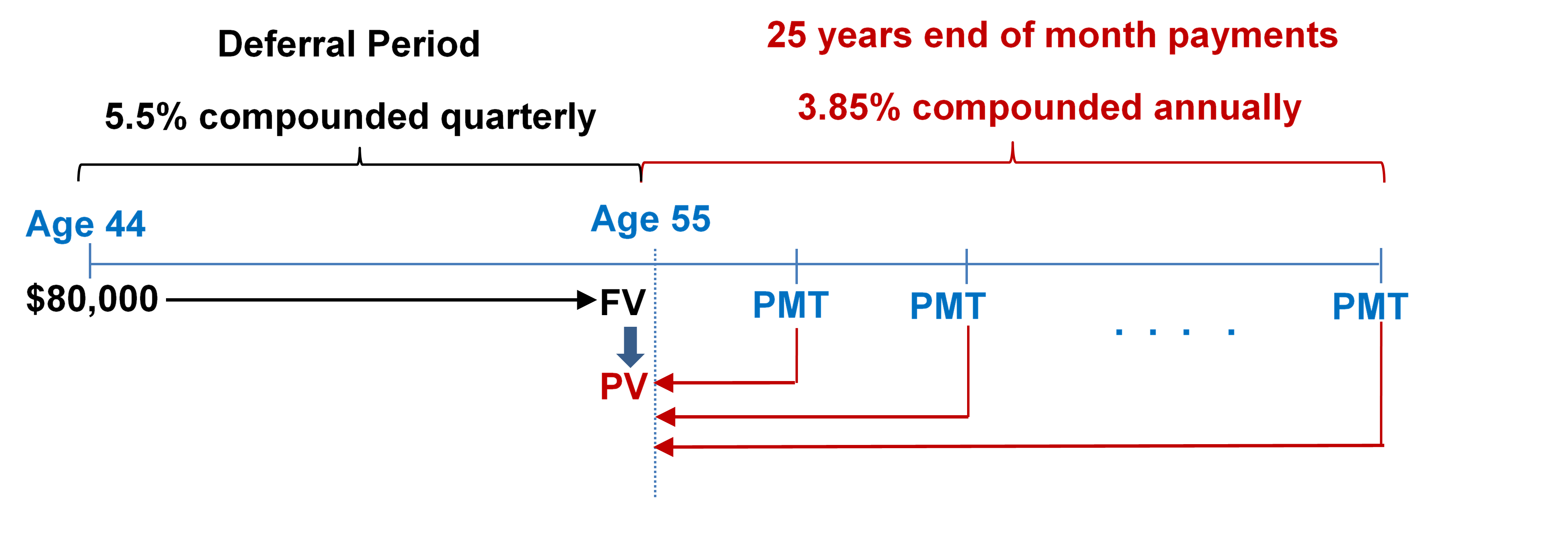
Step 1: Find [latex]FV[/latex].

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 11 \times 4 = 44 \;\text{payments}[/latex]
[latex]I/Y = 5.5[/latex]
[latex]P/Y = 4[/latex]
[latex]C/Y = 4[/latex]
[latex]PV = -80,\!000[/latex]
[latex]PMT = 0[/latex]
[latex]CPT\; FV = \$145,\!897.60\;\text{(This becomes -PV for Step 2)}[/latex]

Step 2: Find [latex]PMT[/latex].

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 25 \times 12 = 300 \;\text{payments}[/latex]
[latex]I/Y = 3.85[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 1[/latex]
[latex]PV = -145,\!897.60[/latex]
[latex]FV =0[/latex]
[latex]CPT\; PV_2 = \$752.78[/latex]

His annuity payments during his retirement will be $752.78 per month.

5. Once Jason graduated college at age 22, he invested $350 into his RRSP at the beginning of every month until age 40. He then stopped his contributions and let the amount earn interest until today, when at age 62 he decided to retire. He wants his retirement money to last until age 85. If his account can earn 10.4% compounded quarterly before age 62 and 4.8% compounded annually after that, how much money can he expect to receive at the end of every quarter?

Solution:

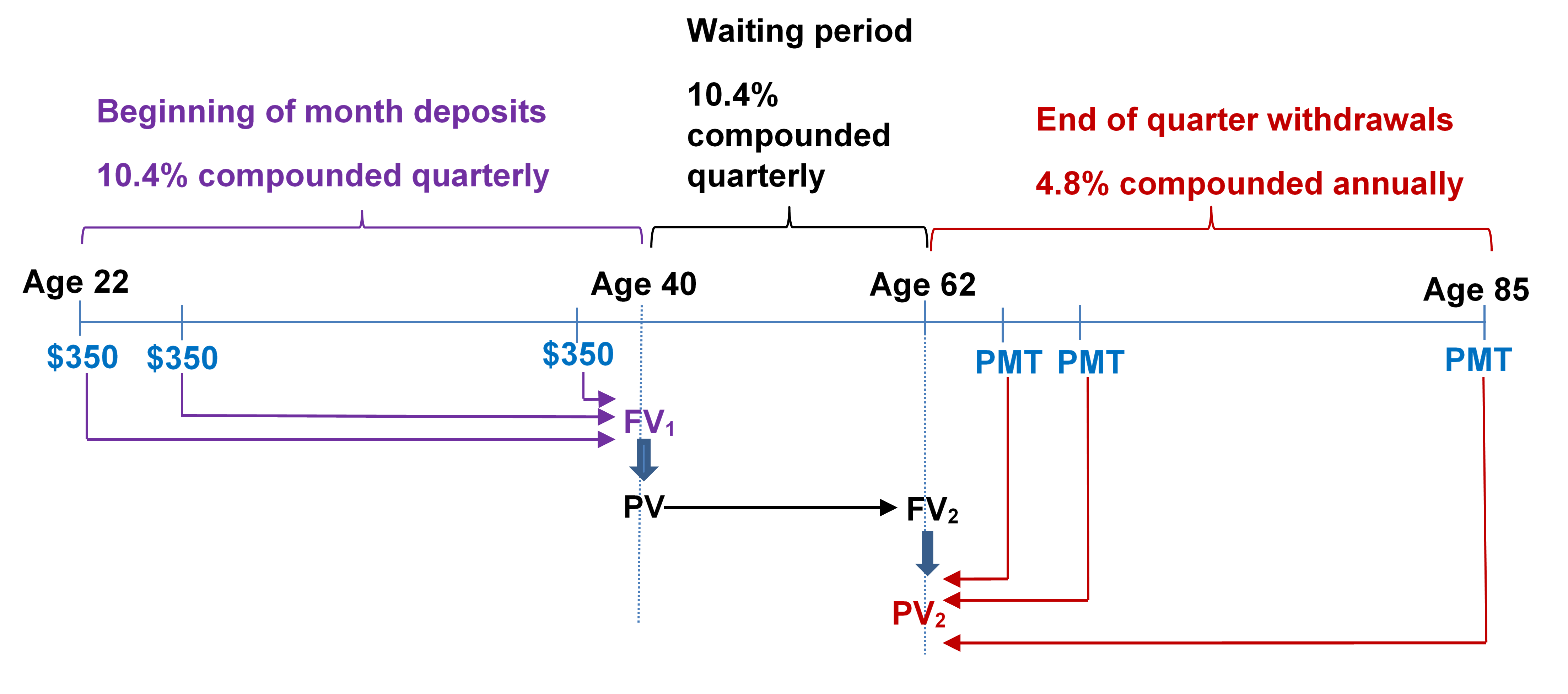
Step 1: Find [latex]FV_1[/latex].

Mode = BGN

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 18 \times 12 = 216 \;\text{payments}[/latex]
[latex]I/Y = 10.4[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 4[/latex]
[latex]PV = 0[/latex]
[latex]PMT = -350[/latex]
[latex]CPT\; FV_1 = \$219,\!693.6683\;\text{This becomes -PV for Step 2}[/latex]

Step 2: Find [latex]FV_2[/latex].

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 22 \times 4 = 88 \;\text{payments}[/latex]
[latex]I/Y = 10.4[/latex]
[latex]P/Y = 4[/latex]
[latex]C/Y = 4[/latex]
[latex]PV = -219,\!693.6683[/latex]
[latex]PMT = 0[/latex]
[latex]CPT\; FV_2 =\$2,\!102,\!738.61\;\text{This becomes -PV for Step 3}[/latex]

Step 3: Find [latex]PMT[/latex].

Mode = END

[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 23 \times 4 = 92 \;\text{payments}[/latex]
[latex]I/Y = 4.8[/latex]
[latex]P/Y = 4[/latex]
[latex]C/Y = 1[/latex]
[latex]FV = 0[/latex]
[latex]PV_2 = -2,\!102,\!738.61[/latex]
[latex]CPT\; PMT =\$37,\!571.53[/latex]

His annuity payments during his retirement will be $37,571.53 per quarter.

Image Descriptions

Figure 12.1.1: Timeline showing deferral period from today until 17 years at 6.7% compounded semi-annually. Starting at 17 years, 10 years of beginning of month payments of $1250 at 4.78% compounded semi-annually. The stream of $1250 payments brought back to 17 years as PV_due.  PV_due brought back to today as PV₂. [Back to Figure 12.1.1]

Figure 12.1.2: Timeline showing deferral period from today until ? at 6.82% compounded monthly. Starting at ?, 5.5 years of beginning of semi-annual period payments of $5000 at 4% compounded quarterly. The stream of $5000 payments brought back to ? as PV_due. PV due brought back to today as PV₂. [Back to Figure 12.1.2]

Figure 12.1.3: Timelineshowing deferral period from August 1, 2014 until August 1, 2024 at 6.6% compounded monthly. Starting at August 1, 2024, 3 years, 9 months of end of month payments of $1000 at 4% compounded quarterly. The stream of $1000 payments brought back to August 1, 2024 as PV₁. PV₁ brought back to August 1, 2014 as PV₂. [Back to Figure 12.1.3]

Figure 12.1.4: Timeline showing deferral period from age 44 until age 55 at 5.5% compounded quarterly. Starting at age 55, 25 years end of month payments of PMT at 3.85% compounded annually. $80,000 at age 44 brought to age 55 as FV. At age 55 the FV becomes the PV for the stream of PMT’s brought back to age 55. [Back to Figure 12.1.4]

Figure 12.1.5: Timeline showing beginning of month deposits of $350 from age 22 until age 40 at 10.4% compounded quarterly. Waiting period from age 40 until age 62 at 10.4% compounded quarterly. Starting at age 62, end of quarter payments of PMT at 4.8% compounded annually until age 85. The stream of $350 deposits brought to age 40 as FV₁. FV₁ at age 40 becomes PV and is brought to age 62 as FV₂. FV₂ becomes PV₂ at age 62 for the stream of PMT’s brought back to age 62. [Back to Figure 12.1.5]