Chapter 10: Solutions to Exercises
10.1: Application: Long-Term GICs
- Sanchez placed $11,930 into a five-year interest payout GIC at 4.2% compounded monthly. Calculate the interest payout amount every month.
Solution:
Step 1: Given information:
[latex]PV = \$11,\!930[/latex];
[latex]\text{Nominal Rate, I/Y}=4.2\%[/latex];
[latex]\text{Compoundings per Year, C/Y} = 12[/latex].
Step 2: Calculate [latex]i[/latex].
[latex]i=\frac{I/Y}{C/Y}=\frac{4.2\%}{12}=0.35\%[/latex]
Step 3: Calculate [latex]n[/latex].
[latex]n= (\text{Number of Years}) \times (\text{Compounds per Year})=5 \times 12=60[/latex]
Step 4: Callculate the future value.
[latex]\begin{align} FV &= PV(1+i)^n\\ &= \$11,\!930(1+0.0035)^{60}\\ &= \$14,\!712.38405 \end{align}[/latex]
Step 5: Find the interest amount earned, [latex]I[/latex].
[latex]I=FV-PV=\$14,\!712.38405-\$11,\!930=2,\!782.38[/latex]
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 60 | 24.2 | −11,930 | 0 | ? | 12 | 12 |
- TD Canada Trust is offering its five-year Stepper GIC at annually escalating rates of 1.15%, 2%, 2.75%, 3.5%, and 4.5%. All rates are compounded semi-annually. Alternatively, it is offering a five-year fixed rate GIC at 2.7% compounded monthly. What total interest amount does an $18,000 investment earn under each option?
Solution:
Calculate the interest on the 5-year Stepper GIC:
Step 1: Given information:
Year 1: I/Y=1.15%; C/Y=2
Year 2: I/Y=2%; C/Y=2
Year 3: I/Y=2.75%; C/Y=2
Year 4: I/Y=3.5%; C/Y=2
Year 5: I/Y=4.5%; C/Y=2
[latex]PV = \$18,\!000[/latex]
Step 2: Calculate [latex]i[/latex].
Year 1: [latex]i = \frac{I/Y}{C/Y}=\frac{1.15\%}{2} = 0.575\%[/latex]
Year 2: [latex]i =\frac{I/Y}{C/Y}= \frac{2\%}{2} = 1\%[/latex]
Year 3: [latex]i =\frac{I/Y}{C/Y}= \frac{2.75\%}{2} = 1.375\%[/latex]
Year 4: [latex]i =\frac{I/Y}{C/Y}= \frac{3.5\%}{2} = 1.75\%[/latex]
Year 5: [latex]i =\frac{I/Y}{C/Y}= \frac{4.5\%}{2} = 2.25\%[/latex]
Step 3: Calculate [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year})[/latex]
For all years: [latex]n = 1 \times 2 = 2[/latex]
Step 4: Calculate the future value for each time segment.
Year 1: [latex]FV = \$18,\!000 (1+0.00575)^2 = \$18,\!207.59513[/latex]
Year 2: [latex]FV = \$18,\!207.59513 (1+0.01)^2 = \$18,\!573.56779[/latex]
Year 3: [latex]FV = \$18,\!573.56779 (1+0.01375)^2 = \$19,\!087.85247[/latex]
Year 4: [latex]FV = \$19,\!087.85247 (1+0.0175)^2 = \$19,\!761.77296[/latex]
Year 5: [latex]FV = \$19,\!761.77296 (1+0.0225)^2 = \$20,\!661.06[/latex]
Step 5: Calculate the amount of interest, [latex]I[/latex].
[latex]\begin{align} I &= FV − PV\\ &= \$20,\!661.06 − \$18,\!000\\ &= $2,\!661.06 \end{align}[/latex]
| Calculation | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Year 1 | 2 | 1.15 | −18,000 | 0 | ? | 2 | 2 |
| Year 2 | 2 | 2 | ±FV from above | 0 | ? | 2 | 2 |
| Year 3 | 2 | 2.75 | ±FV from above | 0 | ? | 2 | 2 |
| Year 4 | 2 | 3.5 | ±FV from above | 0 | ? | 2 | 2 |
| Year 5 | 2 | 4.5 | ±FV from above | 0 | ? | 2 | 2 |
Calculate the Interest on the Fixed Rate GIC:
Step 1: Given information.
[latex]PV = \$18,\!000[/latex]; [latex]I/Y = 2.7\%[/latex]; [latex]C/Y = 12[/latex]; [latex]t = 5\; \text{years}[/latex].
Step 2: Calculate [latex]i[/latex].
[latex]i=\frac{I/Y}{C/Y}=\frac{2.7\%}{12}=0.225\%[/latex]
Step 3: Calculate [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year})[/latex]
[latex]n= 5 \times 12 = 60[/latex]
Step 4: Calculate the future value.
[latex]\begin{align} FV &= PV(1+i)^n\\ & = \$18,\!000(1+0.00225)^{60}\\ &= \$20,\!598.54 \end{align}[/latex]
Step 5: Calculate the amount of interest, [latex]I[/latex].
[latex]\begin{align} I &= FV − PV\\ &= \$20,\!598.54 − \$18,\!000\\ &= \$2,\!598.54 \end{align}[/latex]
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 60 | 2.7 | −18,000 | 0 | ? | 12 | 12 |
- Calculate the interest earned on each of the following five-year GICs. Rank the GICs from best to worst based on the amount of interest earned on a $15,000 investment.
a) An interest payout GIC earning 4.5% compounded quarterly.
b) A fixed rate compound interest GIC earning 4.2% compounded monthly.
c) A variable rate quarterly compound interest GIC earning consecutively 3.9% for 1.5 years, 4.25% for 1.75 years, 4.15% for 0.75 years, and 4.7% for 1 year.
d) An escalator rate GIC earning semi-annually compounded rates of 1.25%, 2%, 3.5%, 5.1%, and 7.75% in successive years.
Solution:
a)
Step 1: Given information.
[latex]PV = \$15,\!000[/latex]; [latex]I/Y = 4.5\%[/latex]; [latex]C/Y = 4[/latex]; [latex]\text{t} = 5\; \text{years}[/latex]
Step 2: Find [latex]i[/latex].
[latex]i=\frac{I/Y}{C/Y}=\frac{4.5\%}{4}=1.125\%[/latex]
Step 3: Find the total interest amount.
[latex]\begin{align} I &= PV \times i\\ & = \$15,\!000 \times 0.01125\\ &= \$168.75 \end{align}[/latex]
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year})[/latex]
[latex]n= 5 \times 4 = 20[/latex]
[latex]\text{Total interest} = \$168.75 \times 20 =\$3,\!375[/latex]
b)
Step 1: Given information.
[latex]PV = \$15,\!000[/latex]; [latex]I/Y = 4.2\%[/latex]; [latex]C/Y = 12[/latex]; [latex]\text{t} = 5\; \text{years}[/latex]
Step 2: Find [latex]i[/latex].
[latex]i=\frac{I/Y}{C/Y}=\frac{4.2\%}{12}=0.35\%[/latex]
Step 3: Find [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year})[/latex]
[latex]n= 5 \times 12 = 60[/latex]
Step 4: Calculate the future value.
[latex]\begin{align} FV &= PV(1+i)^n\\ &= \$15,\!000(1+0.0035)^{60}\\ &= \$18,\!498.39 \end{align}[/latex]
Step 5: Calculate the amount of interest, [latex]I[/latex].
[latex]\begin{align} I &= FV – PV\\ &= \$18,\!498.39 − \$15,\!000\\ &=\$3,\!498.39 \end{align}[/latex]
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 60 | 4.2 | −15,000 | 0 | ? | 12 | 12 |
c)
First Time Segment (today to 1.5 years):
[latex]i = \frac{I/Y}{C/Y}=\frac{3.9\%}{4} =0.975\%[/latex]
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = 1\frac{1}{2} \times 4 = 6[/latex]
[latex]FV_1 = \$15,\!000 (1 + 0.00975)^6 = \$15,\!899.16916[/latex]
Second Time Segment (1.5 years to 3.25 years):
[latex]i = \frac{I/Y}{C/Y}=\frac{4.25\%}{4} = 1.0625\%[/latex]
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = 1\frac{3}{4} \times 4 = 7[/latex]
[latex]FV_2 = \$15,\!899.16916 (1 + 0.010625)^7 = \$17,\!120.03668[/latex]
Third Time Segment (3.25 years to 4 years):
[latex]i = \frac{I/Y}{C/Y}=\frac{4.15\%}{4} = 1.0375\%[/latex]
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = 0.75 \times 4 = 3[/latex]
[latex]FV_3=\$17,\!120.03668 (1 + 0.010375)^3 = \$17,\!658.44538[/latex]
Fourth Time Segment (last year):
[latex]i = \frac{I/Y}{C/Y}=\frac{4.7\%}{4}= 1.175\%[/latex]
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = 1 \times 4 = 4[/latex]
[latex]FV_4 = \$17,\!658.44538 (1 + 0.01175)^4 = \$18,\!503.13505[/latex]
[latex]\begin{align} I &= FV – PV\\ &=\$18,\!503.14 − \$15,\!000\\ &= \$3,\!503.14 \end{align}[/latex]
| Calculation | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1st segment | 6 | 3.9 | −15,000 | 0 | ? | 4 | 4 |
| 2nd segment | 7 | 4.25 | ±FV from above | 0 | ? | 4 | 4 |
| 3rd segment | 3 | 4.15 | ±FV from above | 0 | ? | 4 | 4 |
| 4th segment | 4 | 4.7 | ±FV from above | 0 | ? | 4 | 4 |
d)
Step 1: Given information:
Year 1: I/Y=1.25%; C/Y=2
Year 2: I/Y=2%; C/Y=2
Year 3: I/Y=3.5%; C/Y=2
Year 4: I/Y=5.1%; C/Y=2
Year 5: I/Y=7.75%; C/Y=2
Step 2: For all years:
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = 1 \times 2 = 2[/latex]
Year 1: [latex]i = \frac{I/Y}{C/Y}=\frac{1.25\%}{2} = 0.625\%[/latex]
Year 2: [latex]i = \frac{I/Y}{C/Y}=\frac{2\%}{2} = 1\%[/latex]
Year 3: [latex]i = \frac{I/Y}{C/Y}=\frac{3.5\%}{2} = 1.75\%[/latex]
Year 4: [latex]i = \frac{I/Y}{C/Y}=\frac{5.1\%}{2} = 2.55\%[/latex]
Year 5: [latex]i = \frac{I/Y}{C/Y}=\frac{7.75\%}{2} = 3.875\%[/latex]
Step 3: Calculate the future value for each time segment.
Year 1: [latex]FV = \$15,\!000(1+0.00625)^2 = \$15,\!188.08594[/latex]
Year 2: [latex]FV = \$15,\!188.08594 (1+0.01)^2 = \$15,\!493.36646[/latex]
Year 3: [latex]FV = \$15,\!493.36646 (1+0.0175)^2 = \$16,\!040.37913[/latex]
Year 4: [latex]FV = \$16,\!040.37913 (1+0.0255)^2 = \$16,\!868.86873[/latex]
Year 5: [latex]FV = \$16,\!868.86873 (1+0.03875)^2 = \$18,\!201.54[/latex]
[latex]\begin{align} I &= FV – PV\\ &= \$18,\!201.54 − \$15,\!000\\ &= \$3,\!201.54 \end{align}[/latex]
Calculator Instructions:
| Calculation | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Year 1 | 2 | 1.25 | −15,000 | 0 | ? | 2 | 2 |
| Year 2 | 2 | 2 | ±FV from above | 0 | ? | 2 | 2 |
| Year 3 | 2 | 3.5 | ±FV from above | 0 | ? | 2 | 2 |
| Year 4 | 2 | 5.1 | ±FV from above | 0 | ? | 2 | 2 |
| Year 5 | 2 | 7.75 | ±FV from above | 0 | ? | 2 | 2 |
| Rank | Option | Interest Earned |
|---|---|---|
| 1 | C | $3,503.14 |
| 2 | B | $3,498.39 |
| 3 | A | $3,375.00 |
| 4 | D | $3,201.54 |
10.2: Application: Long-Term Promissory Notes
- Determine the proceeds of the sale on a six-year interest-bearing promissory note for $5,750 at 6.9% compounded monthly, discounted two years and three months before its due date at a discount rate of 9.9% compounded quarterly.
Solution:
Step 1: The timeline below represents the situation.
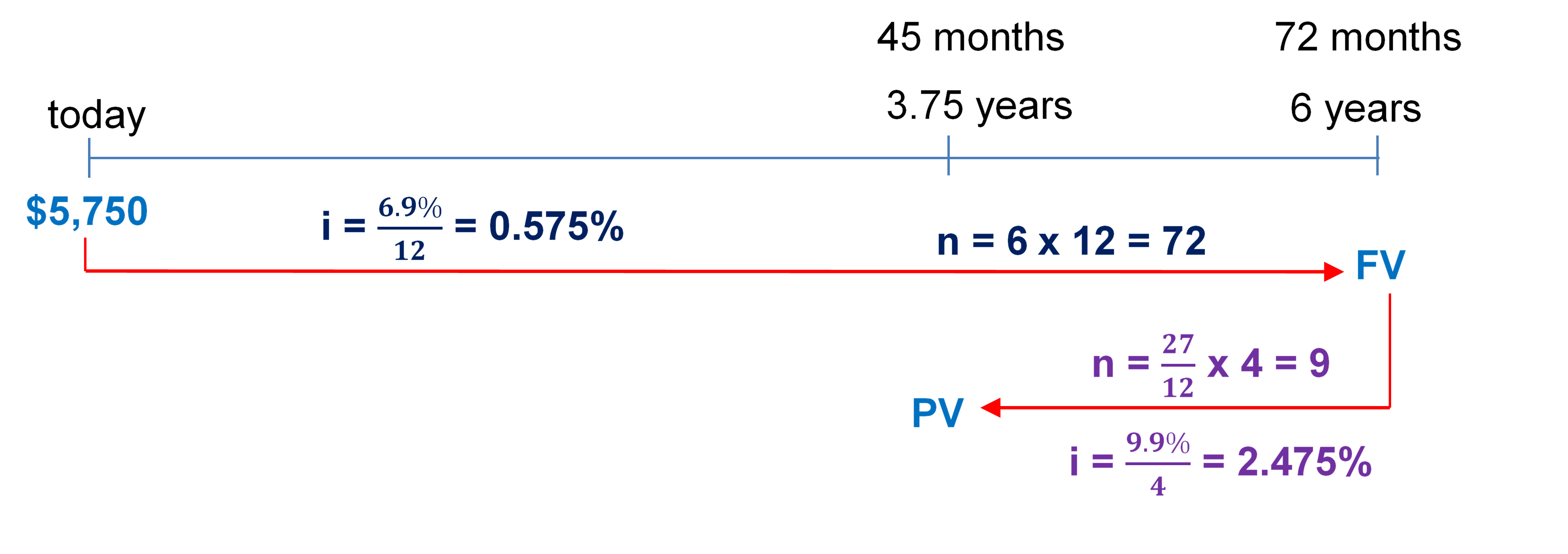
Step 2: Calculate the maturity value (FV) of the original note.
[latex]i = \frac{I/Y}{C/Y}=\frac{6.9\%}{12}= 0.575\%[/latex]
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = 6 \times 12 = 72[/latex]
[latex]\begin{align} FV &= PV(1+i)^n\\ &= \$5,\!750(1+0.00575)^{72}\\ &= \$8,\!688.62 \end{align}[/latex]
Step 3: Find the proceeds by discounting the original note back 2.25 years to 3.75 years. Proceeds = PV.
[latex]i = \frac{I/Y}{C/Y}=\frac{9.9\%}{4}= 2.475\%[/latex]
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = \frac{27}{12} \times 4 = 9[/latex]
[latex]\begin{align} PV&=\frac{FV}{(1+i)^n}\\ &=\frac{\$8,\!688.62}{(1.02475)^9}\\ &=\$6,\!972.52 \;\text{(Proceeds)} \end{align}[/latex]
The proceeds are $6,972.52.
| Action | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Original Note | 72 | 6.9 | −5,750 | 0 | ? | 12 | 12 |
| Proceeds | 9 | 9.9 | ? | 0 | 8,688.62 | 4 | 4 |
- A $36,555 interest-bearing note at 5% compounded monthly is issued on October 15, 2011, for a term of 87 months. Fifty-seven months later, the note is sold to yield a discount amount of $11,733.41. What quarterly compounded discount rate is being used?
Solution:
Step 1: The timeline below represents the situation.
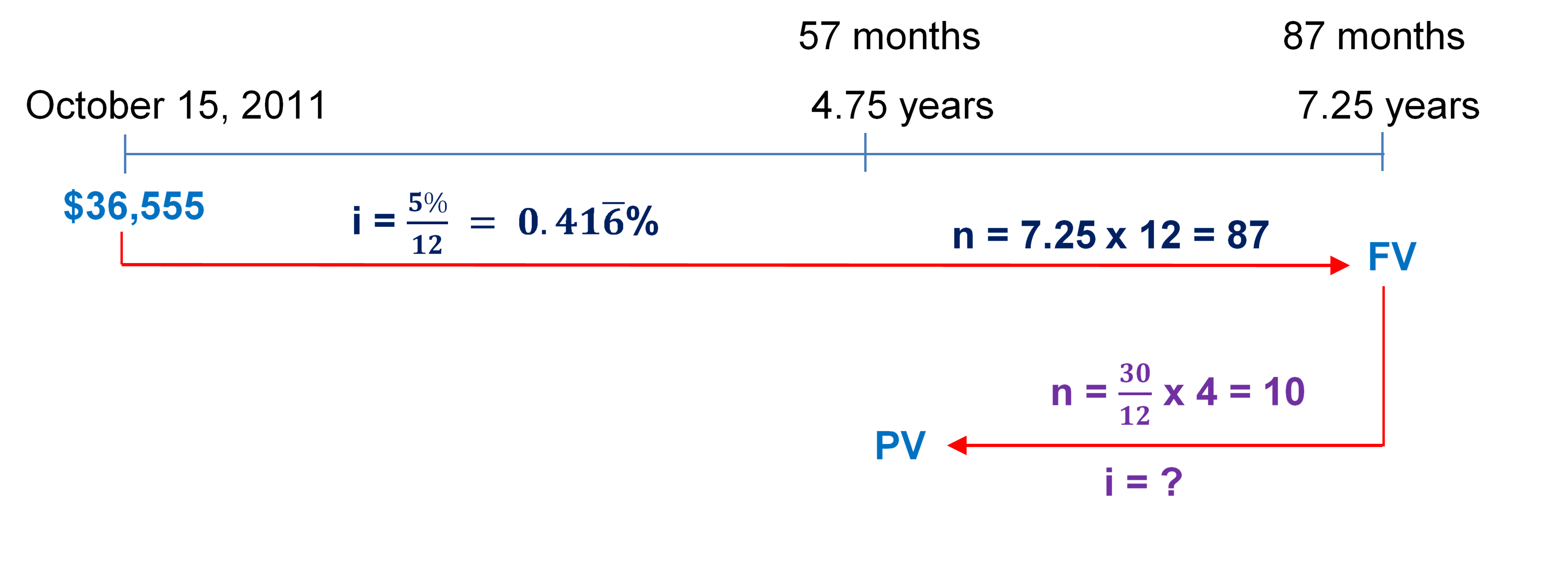
Step 2: Calculate the maturity value (FV) of the original note.
[latex]i = \frac{I/Y}{C/Y}=\frac{5\%}{12}= 0.41\overline{6}\%[/latex]
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = 7.25 \times 12 = 87[/latex]
[latex]\begin{align} FV &= PV(1+i)^n\\ &= \$36,\!555(1+0.0041\overline{6})^{87}\\ &= \$52,\!486.97 \end{align}[/latex]
Step 3: Find the proceeds by discounting the original note back 2.5 years to 4.75 years. Proceeds = PV
[latex]\begin{align} PV &= FV - \text{Discount amount}\\ &= \$36,\!555 - \$11,\!733.41\\ &= \$40,\!753.56\;\text{(Proceeds)} \end{align}[/latex]
Step 4: Find the interest rate compounded quarterly when the original note discounted back from 87 months to 57 months.
[latex]\begin{align} FV &= PV(1+i)^n\\ \$52,\!486.97 &= \$40,\!753.56 (1+ i)^{10}\\ 1.287911 &= (1+ i)^{10}\\ (1.287911)^{(\frac{1}{10})} &= 1+ i\\ 1.025624 &= 1+ i\\ i &= 0.025624 \;\text{(rate per quarter)} \end{align}[/latex]
[latex]\begin{align} \text{Nominal rate}&=i \times \text{(compounds per year)}\\ &= 0.025624 \times 4\\ &= 0.1025 \end{align}[/latex]
[latex]\text{Interest Per Year} = 10.25\%\; \text{compounded quarterly}[/latex]
| Action | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Original Note | 87 | 5 | −36,555 | 0 | ? | 12 | 12 |
| Discount Rate | 10 | ? | −40,753.56 | 0 | 52,486.97 | 4 | 4 |
- A seven-year interest-bearing note for $19,950 at 8.1% compounded quarterly is issued on January 19, 2006. Four years and 11 months later, the note is discounted at 14.55% compounded monthly. Determine the proceeds on the note and how much interest the original owner of the note realized.
Solution:
Step 1: The timeline below represents the situation.
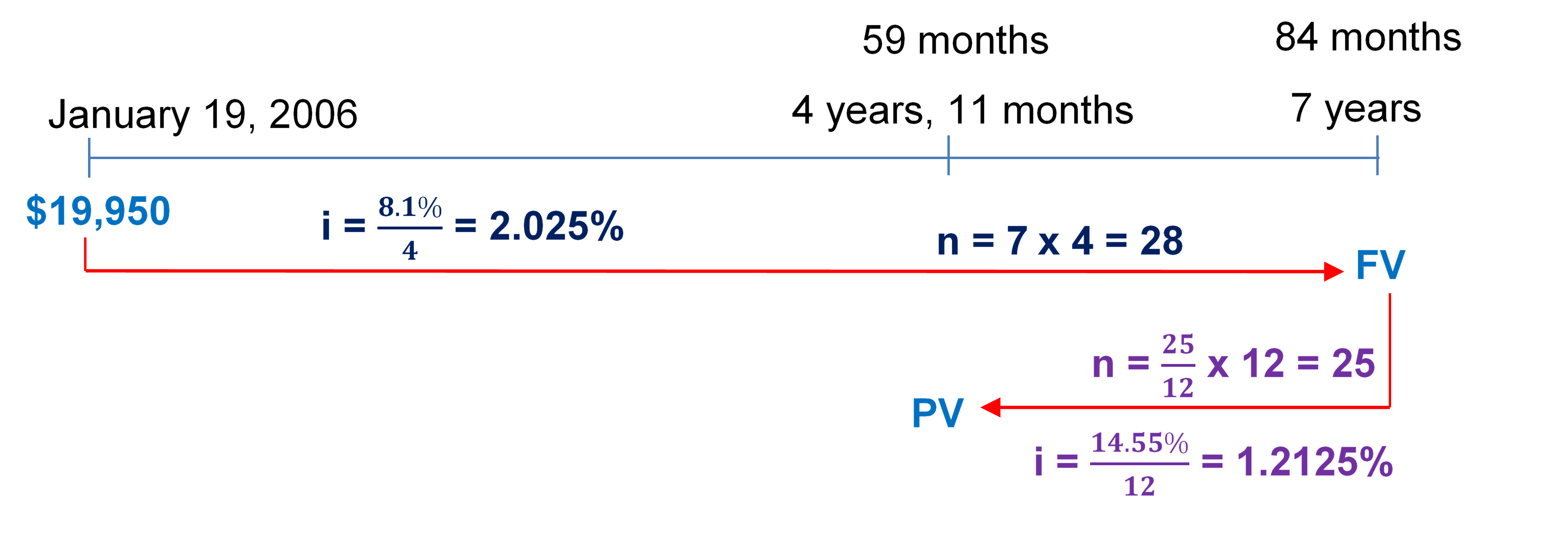
Step 2: Calculate the maturity value (FV) of the original note.
[latex]i = \frac{I/Y}{C/Y}=\frac{8.1\%}{4}= 2.025\%[/latex]
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = 7 \times 4= 28[/latex]
[latex]\begin{align} FV &= PV(1+i)^n\\ &= \$19,\!950(1+0.02025)^{28}\\ &= \$34,\!972.59 \end{align}[/latex]
Step 3: Find the proceeds by discounting the original note back 25 months (84 – 59) to 4 years 11 months.
[latex]\begin{align} PV&=\frac{FV}{(1+i)^n}\\ &=\frac{\$34,\!972.59}{(1.012125)^{25}}\\ &=\$25,\!874.62\;(\text{Proceeds}) \end{align}[/latex]
Calculate the interest amount, [latex]I[/latex].
[latex]\begin{align} I &= FV − PV\\ &= \$25,\!874.62 − \$19,\!950\\ &= \$5,\!924.62 \end{align}[/latex]
Proceeds are $25,874.62 and the interest realized is $5,924.62.
| Action | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Original Note | 28 | 8.1 | −19,950 | 0 | ? | 4 | 4 |
| Proceeds | 25 | 14.55 | ? | 0 | 25,874.62 | 12 | 12 |
10.3: Application: Strip Bonds
- A $15,000 face value Government of Manitoba strip bond has 19.5 years left until maturity. If the current market rate is posted at 6.7322% compounded semi-annually, what is the purchase price for the bond?
Solution:
Note: A Strip Bond is an investment entitling the owner to receive only the face value of the bond at maturity.
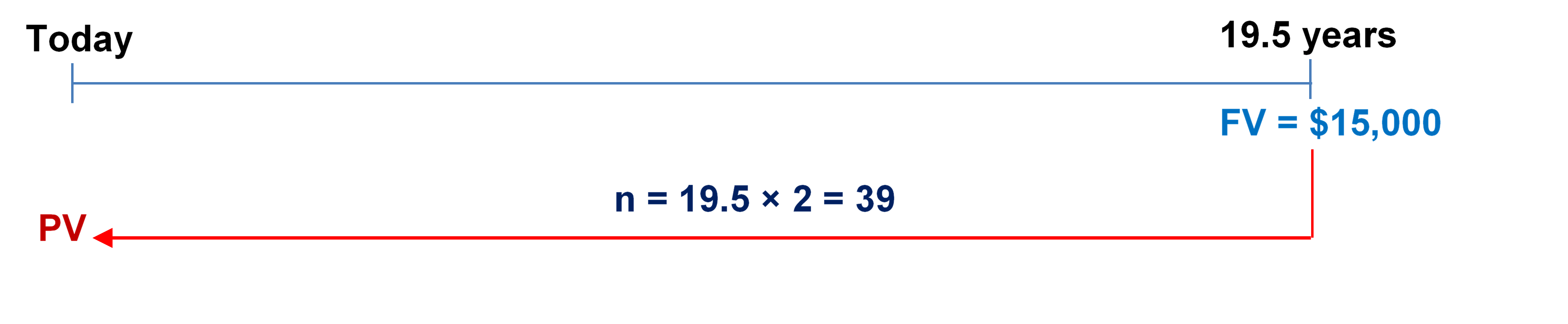
Step 1: Given information:
[latex]FV = \$15,\!000[/latex]; [latex]t = 19.5\;\text{years}[/latex]; [latex]I/Y = 6.7322\%[/latex]; [latex]C/Y = 2[/latex]
Step 2: Calculate [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year}) = 19.5 \times 2 = 39[/latex]
Step 3: Calculate [latex]i[/latex].
[latex]i = \frac{I/Y}{C/Y}=\frac{6.7322\%}{2} = 3.3661\%[/latex]
Step 4: Solve for [latex]PV[/latex].
[latex]\begin{align} PV&=\frac{FV}{(1+i)^n}\\ &=\frac{\$15,\!000}{(1.033661)^{39}}\\ &=\$4,\!124.24 \end{align}[/latex]
The purchase price of the bond is $4,124.24.
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 39 | 6.7322 | ? | 0 | 15,000 | 2 | 2 |
- An investor purchased a $7,500 face value strip bond for $2,686.01 on May 29, 2006. The strip bond had been issued on May 29, 2002, with a 25-year maturity. The investor sold the strip bond on November 29, 2012, for $3,925.28.
a) What was the market yield when the investor purchased the strip bond?
b) What was the market yield when the investor sold the strip bond?
c) What actual yield did the investor realize on the strip bond?
a)

Step 1: Given information:
[latex]PV = \$2,\!686.01[/latex]; [latex]FV = \$7,\!500[/latex]
Step 2: Calculate the number of years.
Number of Years = (May 29, 2027) − (May 29, 2006) = 21
Step 3: Calculate [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year})[/latex]
[latex]n= 21 \times 2= 42[/latex]
Step 4: Calculate [latex]i[/latex].
[latex]\begin{align} FV &= PV(1+i)^n\\ \$7,\!500 &= \$2,\!686.01 (1+ i)^{42}\\ 2.792246 &= (1+ i)^{42}\\ (2.792246)^{(\frac{1}{42})} &= 1+ i\\ 1.024750 &= 1+ i\\ i &= 0.024750 \;\text{(rate per half year)} \end{align}[/latex]
Step 5: Calculate the nominal interest rate, [latex]I/Y[/latex].
[latex]\begin{align} I/Y&= i \times (\text{compounds per year})\\ &= 0.024750 \times 2\\ &= 0.0495 \end{align}[/latex]
[latex]\text{Market yield} = 4.95\%\;\text{compounded semi-annually}[/latex]
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 42 | ? | −2,686.01 | 0 | 7,500 | 2 | 2 |
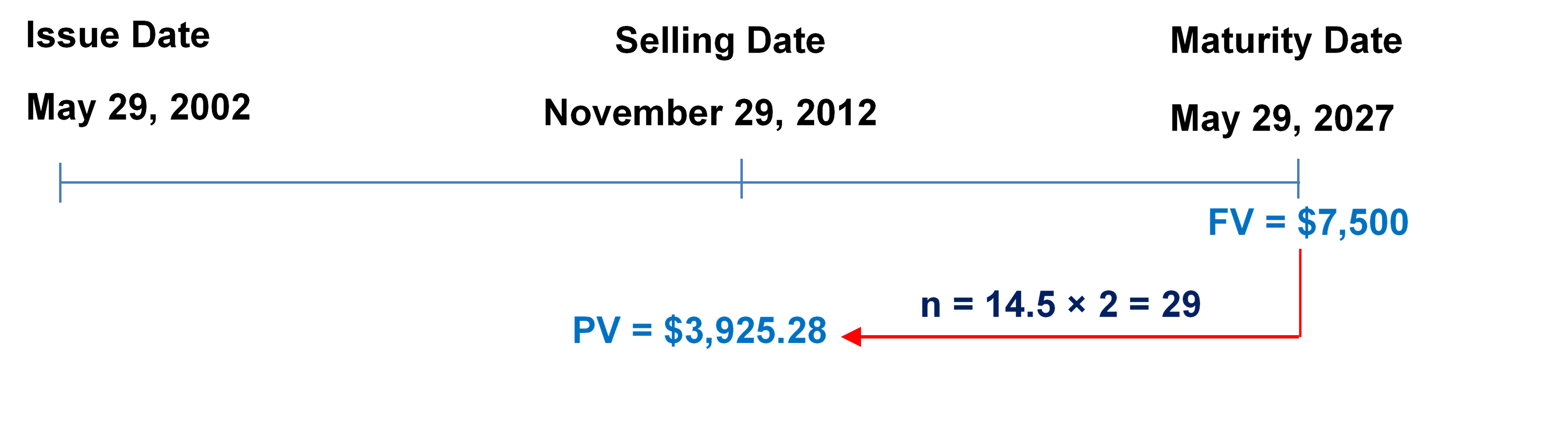
Step 1: Given information:
[latex]PV = \$3,\!925.28[/latex]; [latex]FV = \$7,\!500[/latex]
Step 2: Find the number of years.
Number of Years = (May 29, 2027) − (November 29, 2012) = 14.5
Step 3: Find [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year})[/latex]
[latex]n= 14.5 \times 2= 29[/latex]
Step 4: Find [latex]i[/latex].
[latex]\begin{align} FV &= PV(1+i)^n\\ \$7,\!500 &= \$3,\!925.28 (1+ i)^{29}\\ i &= \left(\frac{\$7,\!500}{\$3,\!925.28}\right)^{\frac{1}{29}}-1\\ i &= 0.022577 \;\text{(rate per half year)} \end{align}[/latex]
Step 5: Calculate the nominal interest rate, [latex]I/Y[/latex].
[latex]\begin{align} \text{Nominal rate}&= i \times (\text{compounds per year})\\ &= 0.022577 \times 2\\ &= 0.045155 \end{align}[/latex]
[latex]\text{Market yield} = 4.5155\%\;\text{compounded semi-annually}[/latex]
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 29 | ? | −3,925.28 | 0 | 7,500 | 2 | 2 |
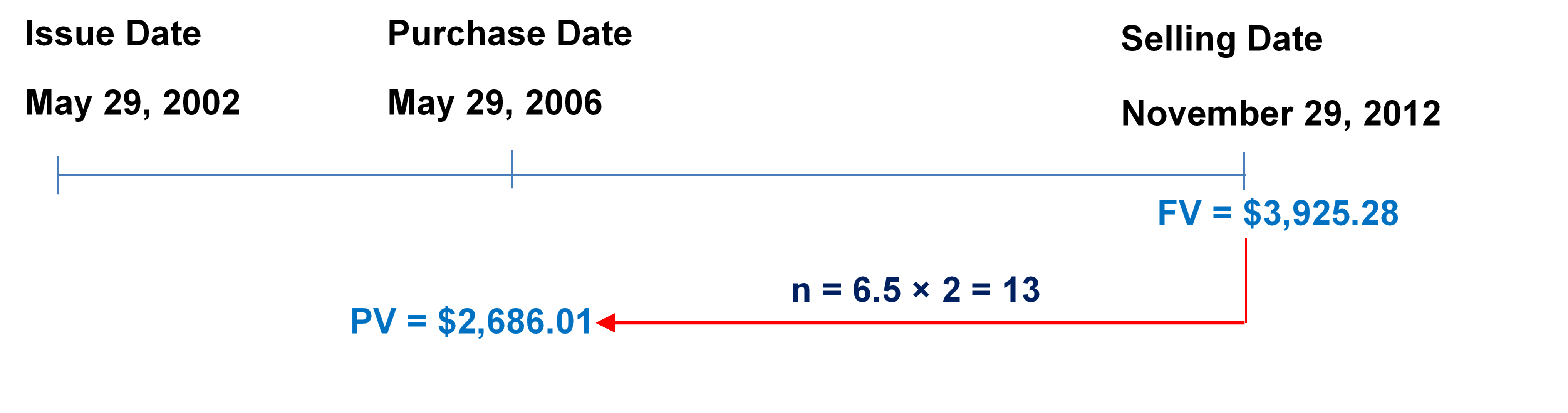
Step 1: Given information:
[latex]PV = \$2,\!686.01[/latex]; [latex]FV = \$3,\!925.28[/latex]
Step 2: Find the number of years.
Number of Years = (November 29, 2012) − (May 29, 2006) = 6.5
Step 3: Find [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times (\text{Compounds Per Year})[/latex]
[latex]n= 6.5 \times 2= 13[/latex]
Step 4: Find [latex]i[/latex].
[latex]\begin{align} FV &= PV(1+i)^n\\ \$3,\!925.28 &= \$2,\!686.01 (1+ i)^{13}\\ i &= \left(\frac{\$3,\!925.28}{\$2,\!686.01}\right)^{\frac{1}{13}}-1\\ i &= 0.029613 \;\text{(rate per half year)} \end{align}[/latex]
Step 5: Calculate the nominal interest rate, [latex]I/Y[/latex].
[latex]\begin{align} \text{Nominal rate}&= i \times (\text{compounds per year})\\ &= 0.029613 \times 2\\ &= 0.059226 \end{align}[/latex]
[latex]\text{Market yield} = 5.9226\%\;\text{compounded semi-annually}[/latex]
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 13 | ? | −2,686.01 | 0 | 3,925.28 | 2 | 2 |
Image Descriptions
Figure 10.2.1: Timeline showing $5,750 moving from today to 72 months (6 years) with i = 6.9%/12 = 0.575% and n = 6 x 12 = 72, giving FV. Then FV from 72 months (6 years) moving back to 45 months (3.75 years) to give PV with n = 27/12 and i = 9.9%/4 = 2.475%. [Back to Figure 10.2.1]
Figure 10.2.2: Timeline showing $36,555 moving from October 15, 2011 to 87 months (7.25 years) with i = 5%/12 = 0.4166666666% and n = 7.25 x 12 = 87, giving FV. Then FV from 87 months (7.25 years) moving back to 57 months (4.75.75 years) to give PV with n = 27/12 and i = ? [Back to Figure 10.2.2]
Figure 10.2.3: Timeline showing $5,750 moving from today to 72 months (6 years) with i = 6.9%/12 = 0.575% and n = 6 x 12 = 72, giving FV. Then FV from 72 months (6 years) moving back to 45 months (3.75 years) to give PV with n = 27/12 and i = 9.9%/4 = 2.475%. [Back to Figure 10.2.3]
Figure 10.3.1: Timeline showing FV = $15,000 at 19.5 years from today brought back to today using PV and n=19.5 × 2 = 39 [Back to Figure 10.3.1]
Figure 10.3.2a: Timeline showing Issue date of May 29, 2002. FV = $15,000 at Maturity Date of May 29, 2027 brought back to Purchase Date of May 29, 2006 as PV = $2,686.01, with n = 21 × 2 = 42 [Back to Figure 10.3.2a]
Figure 10.3.2b: Timeline showing Issue date of May 29, 2002. FV = $15,000 at Maturity Date of May 29, 2027 brought back to Selling Date of November 29, 2012 as PV = $3,925.28, with n = 14.5 × 2 = 29. [Back to Figure 10.3.2b]
Figure 10.3.2c: Timeline: Issue date of May 29, 2002. FV = $3,925.28 at Selling Date of November 29, 2012 brought back to Purchase Date of May 29, 2006 as PV = $2,686.01, with n = 6.5 × 2 = 13 [Back to Figure 10.3.2c]

