10.1: Application: Long Term GICs
Application: Long Term GICs
Recall that Guaranteed Investment Certificates (GICs) are investments offering a guaranteed rate of interest over a predetermined time period. Whereas short-term GICs in Section 8.3 involved terms less than one year, most long-term GICs range from one to five years. Though terms longer than this are available, they are not very common.
Also recall that Section 8.3 discussed the factors that determine interest rates for short-term GICs. The same factors apply to long-term GICs: To receive the highest interest rate on a GIC, you should still invest a large principal in a non-redeemable GIC for the longest term possible.
The key difference between short- and long-term GICs lies in the compounding of interest. Long-term GICs do not wait until the end of the term for interest on them to appear and be paid out. Rather, in line with the definition of compound interest, a long-term GIC periodically converts the accrued interest into principal throughout the transaction. Although GICs come in many varieties (remember, financial institutions try to market these products attractively to investors), three structures are commonly available:
- Interest Payout GICs. An interest payout GIC uses interest rates that by all appearances you might assume to be compounded periodically since they are listed side-by-side with compound interest rates. In practice, though (and by reading the fine print), you will find that the periodically calculated interest is never added to the principal of the GIC, and in essence the concepts of simple interest are used. Instead, the interest is paid out to the investor (perhaps into a chequing account) and does not actually compound unless the investor takes the interest payment received and invests it in another compounding investment. Interest payout GIC interest rates can take either a fixed or variable format. For example, in an online browsing of long-term GICs you may find a posted rate on a three-year GIC at 2% semi-annually. The fine print and footnotes may show that the interest is paid out on a simple interest basis at the end of each six months.
- Compound Interest GICs. A compound interest GIC uses compound interest rates for which interest is periodically calculated and converted to the principal of the GIC for further compounding. Interest rates can be either fixed or variable.
The Formula
Calculating the interest payment requires a simplification of Formula 9.2B. However, in an interest payout GIC you never add the interest to the principal, so you do not need the [latex]1+[/latex] term in the formula. There is also no future value to calculate, just an interest amount. This changes Formula 9.2B from FV = PV(1+i)n to I = PV × in. Simplifying further, you calculate the interest one compound period at a time, where n = 1. This eliminates the need for the n exponent and establishes Formula 10.1.
[latex]\colorbox{LightGray}{Formula 10.1}\; \color{BlueViolet}{\text{Periodic Interest Amount:}}[/latex]
\[\color{BlueViolet}{I=PV \times i}\]
Interest Payout GIC
How It Works
Follow these steps to calculate the interest payment for an interest payout GIC:
Step 1: Identify the amount of principal invested (PV), the nominal interest rate (I/Y) and interest payout frequency (C/Y).
Step 2: Calculate the periodic interest rate (i) sing the formula
[latex]i=\frac{I/Y}{C/Y}[/latex]
Step 3: Calculate the interest amount (I) per compounding period using Formula 10.1.
[latex]I=PV \times i[/latex]
Important Notes
If the interest rate is variable, you must apply Formula 10.1 to each of the variable interest rates in turn to calculate the interest payment amount in the corresponding time segment. For example, if a $1,000 GIC earns 2% quarterly for the first year and 2.4% monthly for the second year, then in the first year I = $1,000 × [latex]\frac{2\%}{4}[/latex] = $5, and in the second year I = 1,000 × [latex]\frac{2.4\%}{12}[/latex] = $2.
Concept Check:
Example 10.1.1: An Interest Payout GIC
Jackson placed $10,000 into a four-year interest payout GIC earning 5.5% semi-annual interest. Calculate the amount of each interest payment and the total interest earned throughout the term.
Solution:
Step 1: Given information:
PV = $10,000; I/Y = 5.5%; C/Y = 2
Step 2: Calculate the periodic interest rate, [latex]i[/latex].
[latex]i=\frac{I/Y}{C/Y}=\frac{5.5\%}{2}=2.75\%=0.0275[/latex]
Step 3: Calculate the periodic interest amount.
[latex]I=PV \times i=\$10,\!000 \times 0.0275=\$275[/latex]
Step 4: Calculate the total interest.
[latex]n=C/Y \times (\text{Number of Years})=2 \times 4=8[/latex]
[latex]\text{Total interest} =\$275 \times 8=\$2,\!200[/latex].
Every six months, Jackson receives an interest payment of $275. Over the course of four years, these interest payments total $2,200.
Compound Interest GIC
How It Works
Follow these steps to calculate the maturity value of the investment or the compound rate.
Calculating the Maturity Value
Fixed Interest Rate
If the compound interest rate is fixed, then you find the maturity value using the formula FV = PV(1+i)n. These 4 steps were introduced in Section 9.2.
Variable Interest Rate
If the compound interest rate is variable, then you find the maturity value for each segment of the timeline. These 7 steps were also introduced in Section 9.2. Note that in step 5, no principal adjustment needs to be made since only the interest rate variable changes.
Alternative approach:
Since only the interest rate changes, expand the future value formula:
[latex]FV=PV(1+i_1)^{n_1}(1+i_2)^{n_2} (1+i_3)^{n_3} \ldots[/latex]
Calculating the Interest Rate
In the event that the unknown variable is the interest rate, recall the 6 steps that were introduced in Section 9.5.
Example 10.1.2: Calculating the Future (Maturity) Value
Assume an investment of $5,000 is made into a three-year compound interest GIC earning 5% compounded quarterly. Solve for the future (maturity) value.
Solutions:

PV = $5,000; I/Y = 5%; C/Y = 4; Term = 3 years
Step 2: Calculate the periodic interest rate, i.
[latex]i=\frac{I/Y}{C/Y}=\frac{5\%}{4}=1.25\%=0.0125[/latex]
Step 3: Calculate the number of compound periods, n.
[latex]n=C/Y \times \text{(Number of years)}=4 \times 3 =12[/latex]
Step 4: Calculate the maturity value, FV.
[latex]\begin{align} FV&=PV(1+i)^n\\ &=\$5,\!000(1+0.0125)^{12}\\ &=\$5,\!803.77 \end{align}[/latex]
Hence, at maturity the GIC contains $5,803.77, consisting of $5,000 of principal and $803.77 of compound interest.
Concept Check:
Example 10.1.3: How Much Do You Have at Maturity
Andrej invested $23,500 into a three-year variable compound interest GIC. The quarterly compounded interest rate was 3.8% for the first 15 months, 3.7% for the next 12 months, and 3.65% after that. What is the maturity value of Andrej’s GIC?
Solution:
Step 1: The principal, terms, and interest rates are known, as shown in the timeline.
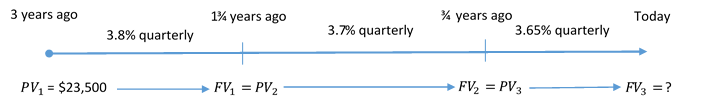
First time segment:
I/Y = 3.8%; C/Y = quarterly = 4; Term = [latex]1\frac{1}{4}[/latex] years
Second time segment:
I/Y = 3.7%; C/Y = quarterly = 4; Term = 1 year
Third time segment:
I/Y = 3.65%; C/Y = quarterly = 4; Term = [latex]\frac{3}{4}[/latex] years
Step 2: For each time segment, calculate the periodic interest rate, i.
First time segment:
[latex]i_1=\frac{3.8\%}{4}=0.95\%=0.0095[/latex]
Second time segment:
[latex]i_2=\frac{3.7\%}{4}=0.925\%=0.00925[/latex]
Third time segment:
[latex]i_3=\frac{3.65\%}{4}=0.9125\%=0.009125[/latex]
Step 3: For each time segment, calculate the number of compound periods, n.
First time segment:
[latex]n_1=4 \times \frac{1}{4}=5[/latex]
Second time segment:
[latex]n_2=4 \times 1=4[/latex]
Third time segment:
[latex]n_3=4 \times \frac{3}{4}=3[/latex]
Step 4: Calculate the future value for the first time segment, FV1.
[latex]FV_1=\$23,\!500(1+0.0095)^5=\$24,\!637.66119[/latex]
This becomes PV2 for the second time segment.
Step 5: Let FV1 = PV2.
Step 6: Calculate the future value for the second time segment, FV2.
[latex]FV_2=\$24,\!637.66119(1+0.00925)^4=\$25,\!561.98119[/latex]
This becomes PV3 for the third time segment.
Repeat Step 5: Let FV2 = PV3.
Repeat Step 6: Calculate the future value for the third line segment, FV3.
[latex]FV_3=\$25,\!561.98119(1+0.009125)^3=\$26,\!268.15[/latex]
Calculator instructions:
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 12 | Answer: 3.729168 | -23500 | 0 | 26,268.15 | 4 | 4 |
Alternative approach:
Expand the future value formula:
[latex]\begin{align} FV&=PV(1+i_1)^{n_1}(1+i_2)^{n_2} (1+i_3)^{n_3} \\ &=\$23,\!500(1+0.0095)^5(1+0.00925)^4(1+0.009125)^3\\ &=\$26,\!268.15 \end{align}[/latex]
At the end of the three-year term compound interest GIC, Andrey has $26,268.15, consisting of the $23,500 principal plus $2,768.15 in interest.
Example 10.1.4: Equivalent Interest Rate on the GIC
Using the previous example, what equivalent fixed quarterly compounded interest rate did Andrej earn on his GIC?
Solution:
Step 1: Given information (from the previous example):
PV = $23,500; FV = $26,268.15; C/Y = 4; Term = 3 years
Step 2: Calculate the total number of compoundings, n.
[latex]n=C/Y \times \text{(Number of Years)}=4 \times 3=12[/latex]
Step 3: Using the future value formula, rearrange and solve for i.
[latex]\begin{align} FV&=PV(1+i)^n\\ \$26,\!268.15&=\$23,\!500(1+i)^{12}\\ 1.117793&=(1+i)^{12}\\ 1.117793^{\frac{1}{12}}&=1+i\\ 1.009322&=1+i\\ i&=0.00932 \end{align}[/latex]
Step 4: Using the formula for i, rearrange and solve for I/Y.
[latex]\begin{align} i&=\frac{I/Y}{C/Y}\\ I/Y&=i \times C/Y\\ &=0.009322 \times 4\\ &=0.037292\; \text{or}\; 3.7292\%\;\text{compounded quarterly} \end{align}[/latex]
Calculator instructions:
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 12 | Answer: 3.729168 | -23,500 | 0 | 26,268.15 | 4 | 4 |
A fixed rate of 3.7292% compounded quarterly is equivalent to the three variable interest rates that Andrej realized.
Escalator Interest GIC
An escalator interest GIC is a compound interest rate GIC with the following characteristics:
- The nominal interest rate always increases with each change so that higher returns on longer terms will encourage the investor to keep the sum of money invested in this GIC.
- The interest rates are known in advance and fixed for the duration of each time segment of the investment.
- Each time segment is most commonly one year in length.
How It Works
The exact same formulas and procedures used for compound interest GICs remain applicable. The most common applications with escalator GICs involve finding one of the following:
- The maturity value of the GIC.
- The equivalent fixed rate of interest on the GIC so that the investor can either compare it to that of other options or just better understand the interest being earned. Recall from Chapter 9 the 6 steps you need to calculate equivalent fixed rates.
Exercises
In each of the exercises that follow, try them on your own. Full solutions are available should you get stuck.
- Sanchez placed $11,930 into a five-year GIC at 4.2% compounded monthly. Calculate the interest amount earned at the end of the five-year term. (Answer: $11,930)
- TD Canada Trust is offering its five-year Stepper GIC at annually escalating rates of 1.15%, 2%, 2.75%, 3.5%, and 4.5%. All rates are compounded semi-annually. Alternatively, it is offering a five-year fixed rate GIC at 2.7% compounded monthly. What total interest amount does an $18,000 investment earn under each option? (Answers: First option: $2,661.06; Second option: $2,598.54)
- Calculate the interest earned on each of the following five-year GICs. Rank the GICs from best to worst based on the amount of interest earned on a $15,000 investment.
a) An interest payout GIC earning 4.5% compounded quarterly. (Answer: $3,375)
b) A fixed rate compound interest GIC earning 4.2% compounded monthly. (Answer: $3,498.39)
c) A variable rate quarterly compound interest GIC earning consecutively 3.9% for 1.5 years, 4.25% for 1.75 years, 4.15% for 0.75 years, and 4.7% for 1 year. (Answer: $3,503.14)
d) An escalator rate GIC earning semi-annually compounded rates of 1.25%, 2%, 3.5%, 5.1%, and 7.75% in successive years. (Answer: $3,201.54)
Calculator instructions for the exercises are included in Solution to Exercises.
Image Descriptions
Figure 10.1.2: Timeline showing PV =$5,000 at Today (on the Left) with an arrow pointing to the end (on the Right) (3 years) where FV = ? and 5% quarterly throughout. [Back to Figure 10.1.2]
Figure 10.1.3: Timeline showing PV1 = $23,500 at 3 years ago moving to 1.75 years ago at 3.8% quarterly to become FV1. At 1.75 years ago, FV1 becomes PV2 which moves to 0.75 year ago at 3.7% quarterly to become FV2. At 0.75 years ago, FV2 becomes PV3 which moves to Today at 3.65% quaterly to become FV3 = ? [Back to Figure 10.1.3]

