Chapter 9: Solution to Exercises
9.1: Compound Interest Fundamentals
- Calculate the periodic interest rate if the nominal interest rate is 7.75% compounded monthly.
Solution:
[latex]\begin{align} \text{Periodic Rate}, i&=\frac{\text{Nominal Rate}}{\text{Compounds per Year}}\\ &=\frac{7.75\%}{12}\\ &= 0.6458\%\;\text{per month} \end{align}[/latex]
The periodic interest rate is 0.65%.
- Calculate the compounding frequency for a nominal interest rate of 9.6% if the periodic interest rate is 0.8%.
Solution:
[latex]\begin{align} \text{Compounds Per Year}, C/Y&=\frac{\text{Nominal Rate}}{\text{Periodic Rate}}\\ &=\frac{9.6\%}{0.8\%}\\ &=12\;(\text{monthly}) \end{align}[/latex]
The compounding frequency is 12 (monthly).
- Calculate the nominal interest rate if the periodic interest rate is 2.0875% per quarter.
Solution:
[latex]\begin{align} \text{Nominal Rate}, I/Y&=(\text{Periodic Rate}) \times (\text{Compounds Per Year})\\ &= 2.0875\% \times 4\\ &=8.35\%\; \text{compounded quarterly} \end{align}[/latex]
The nominal interest rate is 8.35% compounded quarterly.
- After a period of three months, Alese saw one interest deposit of $176.40 for a principal of $9,800. What nominal rate of interest is Alese earning?
Solution:
Step 1: First convert the interest amount into a periodic interest rate per quarter.
[latex]\begin{align} \text{Portion}& = \text{Rate} \times \text{Base}\\ I& = i \times PV\\ \$176.40 &= i \times \$9,\!800\\ i&=\frac{\$176.40}{\$9,\!800}\\ i&=0.018 \;\text{or}\; 1.8\%\; \text{per quarter} \end{align}[/latex]
Step 2: Now convert the result in Step 1 to a nominal rate.
[latex]\begin{align} \text{Nominal Rate, I/Y}&=(\text{Periodic Rate}) \times (\text{Compounds Per Year})\\ &= 1.8\% \times 4\\ &=7.2\%\; \text{compounded quarterly} \end{align}[/latex]
Alese is earning 7.2% compounded quarterly.
9.2: Determining the Future Value
- Find the future value if $53,000 is invested at 6% compounded monthly for 4 years and 3 months.
Solution:
Step 1: Given information:
[latex]PV=\$53,\!000[/latex]; [latex]C/Y=\text{monthly}=12[/latex]; [latex]t=4\frac{3}{12}\;\text{years}[/latex]; [latex]I/Y=6\%[/latex]
Step 2: Find [latex]i[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compound per year (C/Y)}}=\frac{6\%}{12}=0.5\%[/latex]
Step 3: Find [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times C/Y= \left(4\frac{3}{12}\right) \times 12=4.25 \times 12=51[/latex]
Step 4: Solve for [latex]FV[/latex].
[latex]\begin{align} FV &= PV(1 + i)^{51}\\ &= \$53,\!000(1 + 0.005)^{51}\\ &= \$53,\!000(1.005)^{51}\\ &= \$68,\!351.02 \end{align}[/latex]
The future value is $68,351.02.
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 51 | 6 | -53,000 | 0 | ? | 12 | 12 |
- Find the future value if $24,500 is invested at 4.1% compounded annually for 4 years; then 5.15% compounded quarterly for 1 year, 9 months; then 5.35% compounded monthly for 1 year, 3 months.
Solution:
Step 1: Find [latex]FV_1[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{4.1\%}{1}=4.1\%[/latex]
[latex]n = (\text{Number of Years}) \times C/Y=4 \times 1=4[/latex]
[latex]\begin{align} FV_1 &= PV_1(1 + i)^n\\ &= \$24,\!500 (1 + 0.041)^4\\ &= \$24,\!500(1.041)^4\\ &= \$28,\!771.93049\; \text{(This becomes PV for the next calculation in Step 2.)} \end{align}[/latex]
Step 2: Find [latex]FV_2[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{5.15\%}{4}=1.2875\%[/latex]
[latex]n = (\text{Number of Years}) \times C/Y= \left(1\frac{9}{12}\right) \times 4=1.75 \times 4=7[/latex]
[latex]\begin{align} FV_2 &= PV_2(1 + i)^n\\ &= \$28,\!771.93049 (1.012875)^7\\ &= \$31,\!467.33516\; \text{(This becomes PV for the next calculation in Step 3.)} \end{align}[/latex]
Step 3: Find [latex]FV_3[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{5.35\%}{12}=0.4458\overline{3}\%[/latex]
[latex]n = (\text{Number of Years}) \times C/Y= \left(1\frac{3}{12}\right) \times 12=1.25 \times 12=15[/latex]
[latex]\begin{align} FV_3 &= PV_3(1 + i)^n\\ &= \$31,\!467.33516 (1.004458\overline{3})^{15}\\ &= \$33,\!638.67 \end{align}[/latex]
The future value is $33,638.67.
| Step | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 4.1 | -24,500 | 0 | ? | 1 | 1 |
| 2 | 7 | 5.15 | ±(FV from Step 1) | 0 | ? | 4 | 4 |
| 3 | 15 | 5.35 | ±(FV from Step 2) | 0 | ? | 12 | 12 |
- Nirdosh borrowed $9,300 4¼ years ago at 6.35% compounded semi-annually. The interest rate changed to 6.5% compounded quarterly 1¾ years ago. What amount of money today is required to pay off this loan?
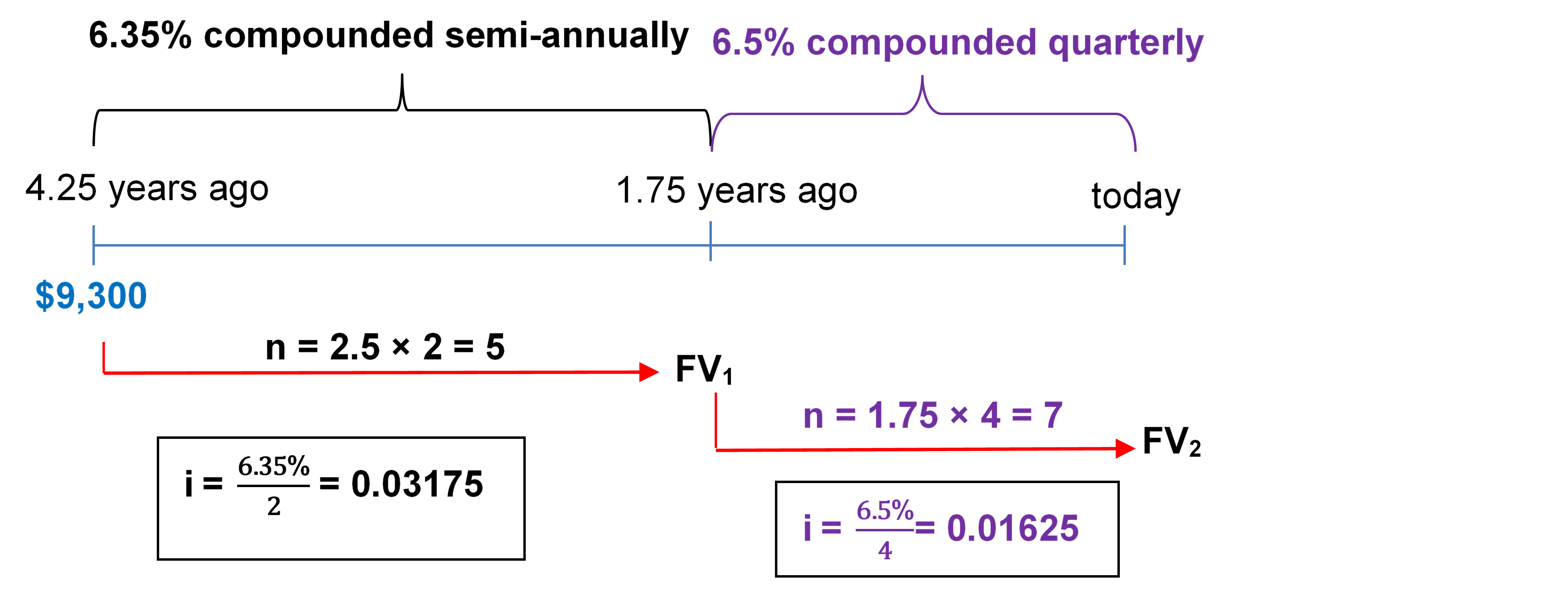
Step 1: Find [latex]FV_1[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{6.35\%}{2}=3.175\%[/latex]
[latex]n=(\text{Number of Years}) \times C/Y=2.5 \times 2=5[/latex]
[latex]\begin{align} FV_ 1&=PV(1 + i)^n\\ &= \$9,\!300(1. 03175)^5\\ &= \$10,\!873.14892\; \text{(This becomes PV for the next calculation in Step 2.)} \end{align}[/latex]
Step 2: Find [latex]FV_2[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{6.5\%}{4}=1.625\%[/latex]
[latex]n = (\text{Number of Years}) \times C/Y=1.75 \times 4=7[/latex]
[latex]\begin{align} FV_ 2&=PV(1 + i)^n\\ &= \$10,\!873.14892(1. 001625)^7\\ &= \$12,\!171.92\; \text{(Round at this step.)} \end{align}[/latex]
It is required today $12,171.92 to pay off the loan.
| Step | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 5 | 6.35 | +9,300 | 0 | ? | 2 | 2 |
| 2 | 7 | 6.5 | ± (FV from Step 1) | 0 | ? | 4 | 4 |
9.3: Determining the Present Value
- A debt of $37,000 is owed 21 months from today. If prevailing interest rates are 6.55% compounded quarterly, what amount should the creditor be willing to accept today?
Solution:
Step 1: Given information:
[latex]FV=\$37,\!000[/latex]; [latex]I/Y= 6.55\%[/latex]; [latex]t=\frac{21}{12}=1.75\;\text{years}[/latex];
[latex]C/Y=\text{quarterly}=4[/latex].
Step 2: Find [latex]i[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{6.55\%}{4}=1.6375\%[/latex]
Step 3: Find [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times C/Y=\frac{21}{12} \times 4=7[/latex]
Step 4: Solve for [latex]PV[/latex].
[latex]\begin{align} PV&=\frac{FV}{(1+i)^n}\\ &=\frac{\$37,\!000}{(1.016375)^7}\\ &=\$33,\!023.56 \end{align}[/latex]
The creditor should be willing to accept $33,023.56 today?
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 7 | 6.55 | ? | 0 | 37,000 | 4 | 4 |
- For the first 4½ years, a loan was charged interest at 4.5% compounded semi-annually. For the next 4 years, the rate was 3.25% compounded annually. If the maturity value was $45,839.05 at the end of the 8½ years, what was the principal of the loan?
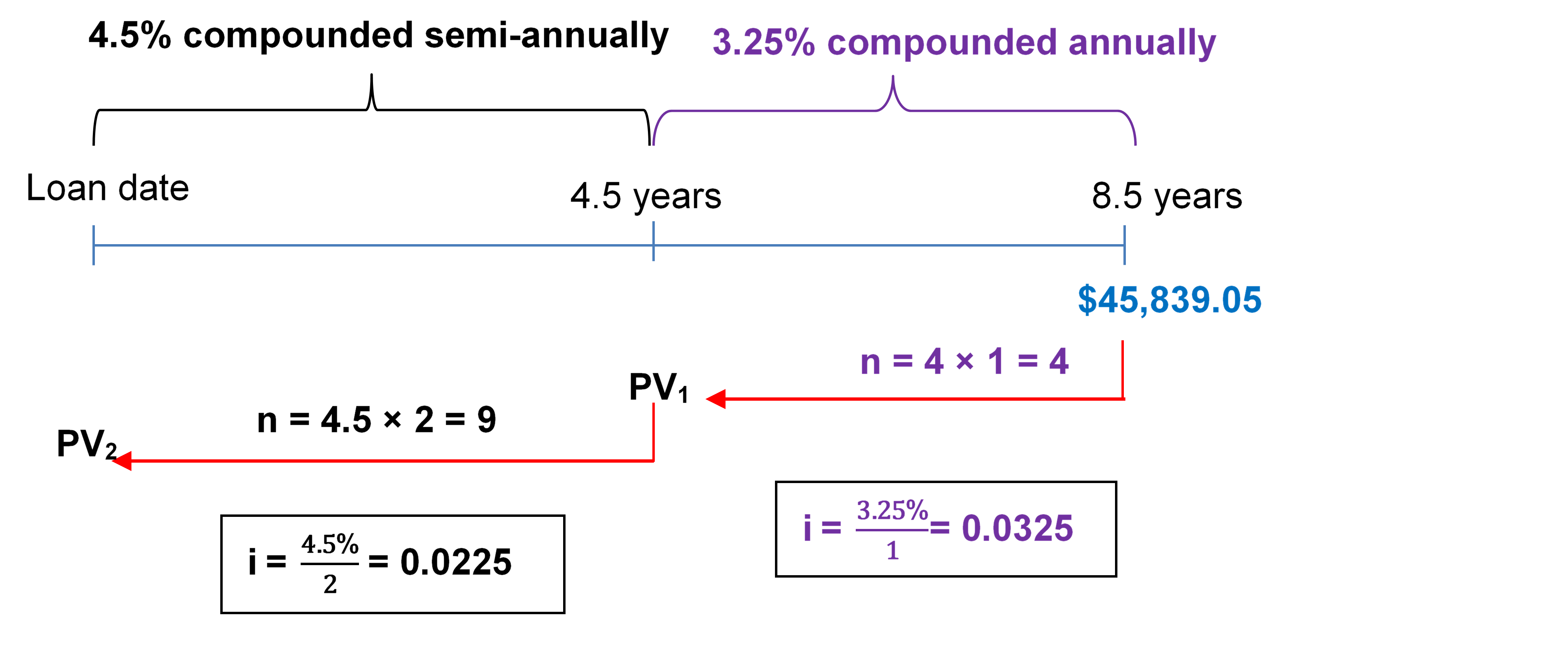
Step 1: Find [latex]PV_1[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{3.25\%}{1}=3.25\%[/latex]
[latex]n = \text{(Number of Years)} \times C/Y=4 \times 1=4[/latex]
[latex]\begin{align} PV_1&=\frac{FV}{(1+i)^n}\\ &=\frac{\$45,\!839.05}{(1.0325)^4}\\ &=\$40,\!334.37829\;\text{(This becomes FV for the next calculation in Step 2.)} \end{align}[/latex]
Step 2: Find [latex]PV_2[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{4.5\%}{2}=2.25\%[/latex]
[latex]n = (\text{Number of Years}) \times C/Y=4.5 \times 2=9[/latex]
[latex]\begin{align} PV_2&=\frac{FV}{(1+i)^n}\\ &=\frac{\$40,\!334.37829}{(1.0225)^9}\\ &=\$33,\!014.56\;\text{(Round at this step.)} \end{align}[/latex]
The principal of the loan is $33,014.56.
| Steps | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 3.25 | ? | 0 | −45,839.05 | 1 | 1 |
| 2 | 9 | 4.5 | ? | 0 | ±(PV from Step 1) | 2 | 2 |
9.4: Equivalent Payments
- A winning lottery ticket offers the following two options:
a) A single payment of $1,000,000 today or
b) $250,000 today followed by annual payments of $300,000 for the next three years.
If money can earn 9% compounded annually, which option should the winner select? How much better is that option in current dollars?
Solution:
a) The $1,000,000 is already today.
b) To fairly compare the payment plan, move all money to today as well.
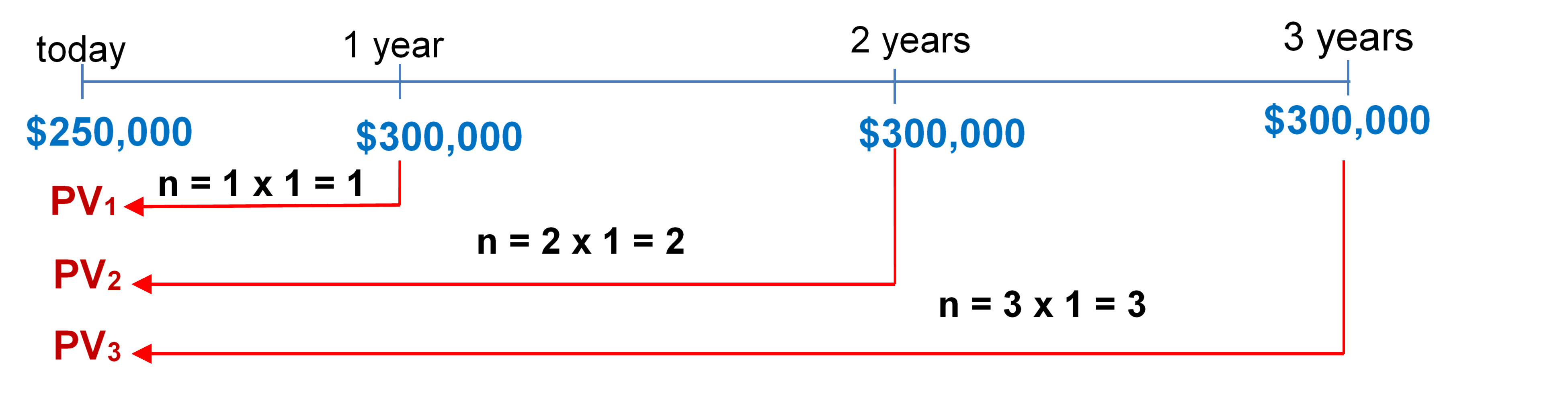
[latex]\text{Focal Date} = \text{Today}[/latex]
Step 1: Find [latex]i[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{9\%}{1}=9\%[/latex]
Step 2: Find [latex]n[/latex] of the payments.
[latex]n= (\text{Number of Years}) \times C/Y[/latex]
Payment #1: [latex]n= 1 \times 1=1[/latex]
Payment #2: [latex]n=2 \times 1=2[/latex]
Payment #3: [latex]n=3 \times 1=3[/latex]
Step 3: Find the present value of the payments.
[latex]\begin{align} PV_1&=\frac{FV}{(1+i)^n}\\ &=\frac{\$300,\!000}{(1.09)^1}\\ &=\$275,\!229.3578 \end{align}[/latex]
[latex]\begin{align} PV_2&=\frac{FV}{(1+i)^n}\\ &=\frac{\$300,\!000}{(1.09)^2}\\ &=\$252,\!503.998 \end{align}[/latex]
[latex]\begin{align} PV_3&=\frac{FV}{(1+i)^n}\\ &=\frac{\$300,\!000}{(1.09)^3}\\ &=\$231,\!655.044 \end{align}[/latex]
[latex]\begin{align} \text{Total Present Value Today}&=\$250,\!000 + \$275,\!229.3578 + \$252,\!503.998 + \$231,\!655.044\\ &=\$1,\!009,\!388.40 \end{align}[/latex]
Payment plan is better by $1,009,388.40 − $1,000,000 = $9,388.40.
| Payment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 9 | ? | 0 | 300,000 | 1 | 1 |
| 2 | 2 | 9 | ? | 0 | 300,000 | 1 | 1 |
| 3 | 3 | 9 | ? | 0 | 300,000 | 1 | 1 |
- James is a debt collector. One of his clients has asked him to collect an outstanding debt from one of its customers. The customer has failed to pay three amounts: $1,600 eighteen months ago, $2,300 nine months ago, and $5,100 three months ago. In discussions with the customer, James finds she desires to clear up this situation and proposes a payment of $1,000 today, $4,000 nine months from now, and a final payment two years from now. The client normally charges 16.5% compounded quarterly on all outstanding debts. What is the amount of the third payment?
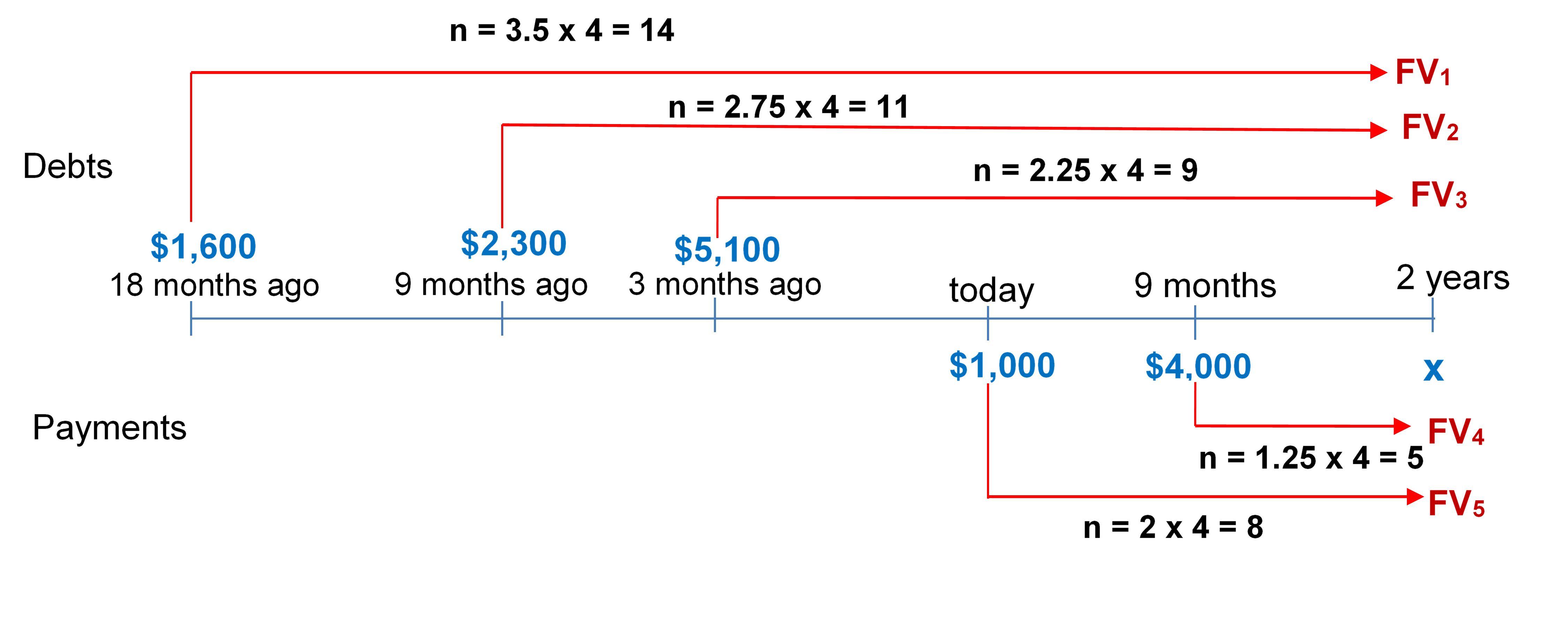
[latex]\text{Focal Date} = 2\; \text{years from today}[/latex]
Step 1: Find [latex]i[/latex].
[latex]i=\frac{\text{Nominal Rate (I/Y)}}{\text{Compounds per Year (C/Y)}}=\frac{16.5\%}{4}=4.125\%[/latex]
Step 2: Find [latex]n[/latex] of the payments.
[latex]n= (\text{Number of Years}) \times C/Y[/latex]
Payment #1: [latex]n=3.5 \times 4=14[/latex]
Payment #2: [latex]n=2.75 \times 4=11[/latex]
Payment #3: [latex]n=2.25 \times 4=9[/latex]
Payment #4: [latex]n=1.25 \times 4=5[/latex]
Payment #5: [latex]n=2 \times 4=8[/latex]
Step 3: Find the future value of the payments.
[latex]FV_1 = \$1,\!600(1+0.04125)^{14} = \$2,\!817.670366[/latex]
[latex]FV_2 = \$2,\!300(1+0.04125)^{11} = \$3,\!587.839398[/latex]
[latex]FV_3 = \$5,\!100(1+0.04125)^{9} = \$7,\!337.790461[/latex]
[latex]FV_4 = \$4,\!000(1+0.04125)^{5} = \$4,\!895.928462[/latex]
[latex]FV_5 = \$1,\!000(1+0.04125)^{8} = \$1,\!381.783859[/latex]
[latex]\begin{align} \text{Total Dated Debts} &= \text{Total Dated Payments}\\ FV_1 + FV_2 + FV_3 &= x + FV_4 + FV_5\\ \$2,\!817.670366 + \$3,\!587.839398 + \$7,\!337.790461 &= x + \$4,\!895.928462 + \$1,\!381.783859\\ \$13,\!743.30023 &= x + \$6,\!277.712321\\ x &= \$7,\!465.59 \end{align}[/latex]
The amount of the third payment is $7,465.59.
| Payment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Original 1 | 14 | 16.5 | 1,600 | 0 | ? | 4 | 4 |
| Original 2 | 11 | 16.5 | 2,300 | 0 | ? | 4 | 4 |
| Original 3 | 9 | 16.5 | 5,100 | 0 | ? | 4 | 4 |
| Proposed 1 | 8 | 16.5 | 1,000 | 0 | ? | 4 | 4 |
| Proposed 2 | 5 | 16.5 | 4,000 | 0 | ? | 4 | 4 |
- Four years ago, Aminata borrowed $5,000 from Randal with interest at 8% compounded quarterly to be repaid one year from today. Two years ago, Aminata borrowed another $2,500 from Randal at 6% compounded monthly to be repaid two years from today. Aminata would like to restructure the payments so that she can pay 15 months from today and 2½ years from today. The first payment is to be twice the size of the second payment. Randal accepts an interest rate of 6.27% compounded monthly on the proposed agreement. Calculate the amounts of each payment assuming the focal date is 15 months from today.
Solution:
First, calculate the amounts owing under Aminata’s original loans.
Original Loan 1:
[latex]i=\frac{I/Y}{C/Y}=\frac{8\%}{4}=2\%[/latex]
[latex]n= (\text{Number of Years}) \times C/Y=5 \times 4=20[/latex]
[latex]\begin{align} FV_1 &= PV(1 + i)^n\\ & = \$5,\!000(1.02)^{20}\\ &=\$7,\!429.74\;\text{(Due in 1 year from today.)} \end{align}[/latex]
Original Loan 2:
[latex]i=\frac{I/Y}{C/Y}=\frac{6\%}{12}=0.5\%[/latex]
[latex]n= (\text{Number of Years}) \times C/Y=4 \times 12=48[/latex]
[latex]\begin{align} FV_2 &= PV(1 + i)^n\\ & = \$2,\!500(1.005)^{48}\\ &=\$3,\!176.22\; \text{(Due in 2 year from today.)} \end{align}[/latex]
| Loan | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 20 | 8 | 5,000 | 0 | ? | 4 | 4 |
| 2 | 48 | 6 | 2,500 | 0 | ? | 12 | 12 |
Now calculate the equivalent payments under the proposed arrangement:
1 year = 12 months
2 years = 24 months
2.5 years = 30 months
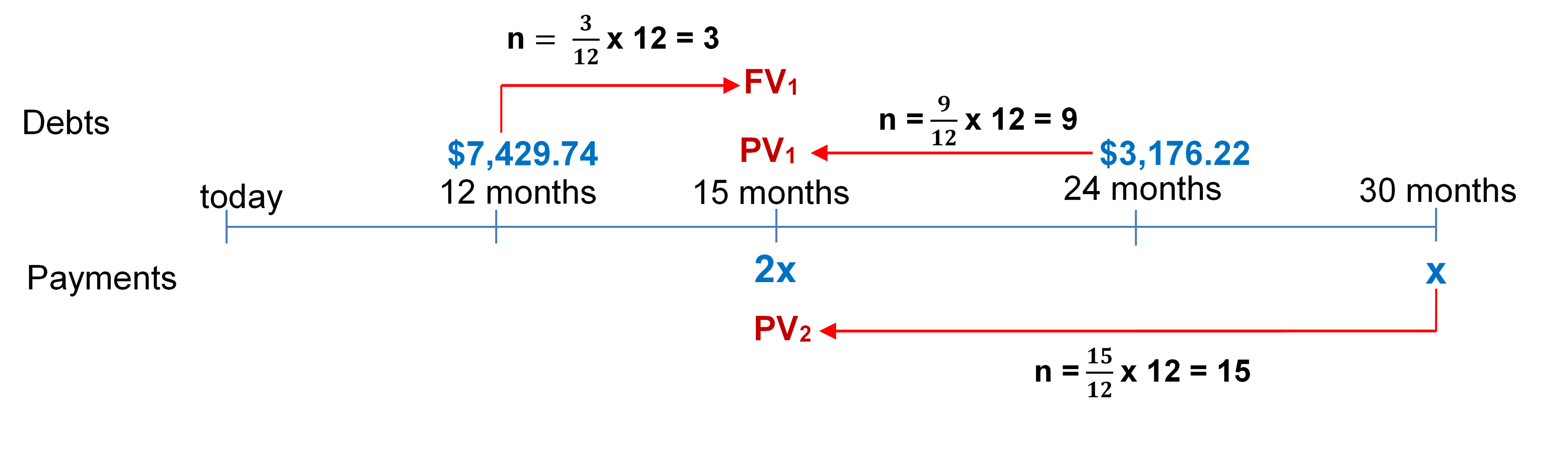
[latex]i=\frac{I/Y}{C/Y}=\frac{6.27\%}{12}=0.5225\%[/latex]
[latex]\begin{align} \text{Total Dated Debts} &= \text{Total Dated Payments}\\ FV_1 + PV_1 &= 2x + PV_2\\ 7,\!429.74 (1.005225)^3 +\frac{3,\!176.22}{(1.005225)^9} &= 2x + \frac{x}{(1.005225)^{15}}\\ 7,\!546.810744 + 3,\!030.686729 &= 2x + 0.924806x\\ \$10,\!577.49747 &= 2.924806x\\ x &= \$3,\!616.48\; \text{(second payment)}\\\\ 2x = 2(\$3,\!616.48) &= $7,\!232.96\; \text{(first payment)} \end{align}[/latex]
The amount of each payment is $7,232.96.
| Payment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Original 1 | 3 | 6.27 | 7,429.74 | 0 | ? | 12 | 12 |
| Original 2 | 9 | 6.27 | ? | 0 | 3,176.22 | 12 | 12 |
| Proposed 1 | 15 | 6.27 | ? | 0 | 1 | 12 | 12 |
9.5 Determining the Interest Rate
- Your company paid an invoice five months late. If the original invoice was for $6,450 and the amount paid was $6,948.48, what monthly compounded interest rate is your supplier charging on late payments?
Solution:
Step 1: Given information:
[latex]PV=\$6,\!450[/latex]; [latex]FV=\$6,\!948.48[/latex]; [latex]C/Y=\text{monthly}=12[/latex]
Step 2: Find [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times C/Y=\frac{5}{12} \times 12=5[/latex]
Step 3: Using the formula for [latex]FV[/latex], rearrange and solve for [latex]i[/latex].
[latex]\begin{align} FV &= PV(1 + i)^n\\ \$6,\!948.48 &= \$6,\!450(1 + i)^5\\ 1.077283 &= (1+i)^5\\ 1.077283^{\frac{1}{5}} &= (1+i)\\ 1.014999 &= 1 + i\\ i& = 0.014999 \end{align}[/latex]
Step 4: Solve for the nominal rate, [latex]I/Y[/latex].
[latex]\begin{align} I/Y&=i \times 12\\ &=0.179999\\ &= 18\% \;\text{(compounded monthly)} \end{align}[/latex]
The supplier is charging 18% compounded monthly on late payments?
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 5 | ? | −6,450 | 0 | 6,948.48 | 12 | 12 |
- At what monthly compounded interest rate does it take five years for an investment to double?
Solution:
Step 1: Pick any two values for PV and FV where FV is double the PV.
[latex]PV = \$10,\!000[/latex]; [latex]FV = \$20,\!000[/latex]
Step 2: Find [latex]n[/latex].
[latex]n = (\text{Number of Years}) \times C/Y=5 \times 12=60[/latex]
Step 3: Using the formula for [latex]FV[/latex] solve for [latex]i[/latex].
[latex]\begin{align} FV &= PV(1 + i)^n\\ \$20,\!000&= \$10,\!000(1 + i)^{60}\\ 2&= (1+i)^{60}\\ 2^{\frac{1}{60}}& = (1+i)\\ 1.011619 &= 1 + i\\ i& = 0.011619 \end{align}[/latex]
Step 4: Solve for the nominal rate, [latex]I/Y[/latex].
[latex]\begin{align} \text{Nominal Rate}&=i \times 12\\ &=0.139428\\ &=13.94\% \;\text{compounded monthly} \end{align}[/latex]
At monthly compounded interest rate does it take five years for an investment to double.
The investment will double in five years at 13.94% compounded monthly.
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 60 | ? | −10,000 | 0 | 20,000 | 12 | 12 |
- Indiana just received a maturity value of $30,320.12 from a semi-annually compounded investment that paid 4%, 4.1%, 4.35%, 4.75%, and 5.5% in consecutive years. What amount of money did Indiana invest? What fixed quarterly compounded nominal interest rate is equivalent to the variable rate his investment earned?
Solution:
Step 1: Given information:
Year 1: I/Y=4\%; C/Y=2
Year 2: I/Y=4.1%; C/Y=2
Year 3: I/Y=4.35%; C/Y=2
Year 4: I/Y=4.75%; C/Y=2
Year 5: I/Y=5.5%; C/Y=2
Step 2: Calculate [latex]n[/latex] and [latex]i[/latex] for all years:
[latex]n = \text{(Number of Years)} \times C/Y=1 \times 2=2[/latex]
Year 1: [latex]i = \frac{I/Y}{C/Y}=\frac{4\%}{2}= 2\%[/latex]
Year 2: [latex]i = \frac{I/Y}{C/Y}=\frac{4.1\%}{2}= 2.05\%[/latex]
Year 3: [latex]i =\frac{I/Y}{C/Y}=\frac{4.35\%}{2}= 2.175\%[/latex]
Year 4: [latex]i = \frac{I/Y}{C/Y}=\frac{4.75\%}{2}= 2.375\%[/latex]
Year 5: [latex]i = \frac{I/Y}{C/Y}=\frac{5.5\%}{2}= 2.75\%[/latex]
Step 3: Solve for [latex]PV[/latex].
Year 5: [latex]\begin{align}PV=\frac{\$30,320.12}{(1+0.0275)^2} = \$28,\!718.86385\end{align}[/latex]
Year 4: [latex]\begin{align}PV =\frac{\$28,718.86385}{(1+0.02375)^2} = \$27,\!401.82101\end{align}[/latex]
Year 3: [latex]\begin{align}PV = \frac{\$27,401.82101}{(1+0.02175)^2} = \$26,\!247.63224\end{align}[/latex]
Year 2: [latex]\begin{align}PV = \frac{\$26,247.63224}{(1+0.0205)^2} = \$25,\!203.68913\end{align}[/latex]
Year 1: [latex]\begin{align}PV = \frac{\$25,203.68913}{(1+0.02)^2} = \$24,\!225\end{align}[/latex]
Step 4: Solve for [latex]n[/latex].
[latex]n = \text{(Number of Years)} \times C/Y= 5\times 4=20[/latex]
Step 5: Use the formula for [latex]FV[/latex] and rearrange for [latex]i[/latex].
[latex]\begin{align} FV &= PV(1 + i)^n\\ \$30,\!320.12& = \$24,\!225(1+i)^{20}\\ 1.251604 &= (1+i)^{20}\\ 1.251604^{\frac{1}{20}}&= 1+i\\ 1.011284 &= 1+i\\ i &= 0.011284 \end{align}[/latex]
Step 6: Find the nominal rate, [latex]I/Y[/latex].
[latex]\begin{align} I/Y&=i \times C/Y\\ &=0.011284 \times 4\\ &= 0.045138\\ &=4.51\%\; \text{compounded quarterly} \end{align}[/latex]
$24,225 investment earned 4.51% compounded quarterly.
| Calculation | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Year 5 | 2 | 5.5 | ? | 0 | 30,320.12 | 2 | 2 |
| Year 4 | 2 | 4.75 | ? | 0 | ±PV from above | 2 | 2 |
| Year 3 | 2 | 4.35 | ? | 0 | ±PV from above | 2 | 2 |
| Year 2 | 2 | 4.1 | ? | 0 | ±PV from above | 2 | 2 |
| Year 1 | 2 | 4 | ? | 0 | ±PV from above | 2 | 2 |
| Nominal rate | 20 | ? | −24,225 | 0 | 30,320.12 | 4 | 4 |
9.6: Equivalent and Effective Interest Rates
- The HBC credit card has a nominal interest rate of 26.44669% compounded monthly. What effective rate is being charged?
Solution:
Step 1: Given information:
[latex]I/Y = 26.44669\%[/latex]; [latex]C/Y_{\text{Old}} = 12[/latex]; [latex]C/Y_{\text{New}} = 1[/latex]
Step 2:
[latex]\begin{align} i_{\text{Old}} &= \frac{I/Y}{C/Y_{\text{Old}}}\\ &= \frac{26.44669\%}{12}\\ &= 2.203890\% \end{align}[/latex]
Step 3:
[latex]\begin{align} i_{\text{New}}&=(1+i_{\text{Old}})^{\frac{C/Y_{\text{Old}}}{C/Y _{\text{New}}}}-1\\ &=(1+0.02203890)^{\frac{12}{1}}-1\\ &=(1.02203890)^{12}-1\\ &=1.299-1\\ &=0.299 \end{align}[/latex]
29.9% effectively
| NOM | C/Y | EFF |
|---|---|---|
| 26.44669 | 12 | ? |
- Louisa is shopping around for a loan. TD Canada Trust has offered her 8.3% compounded monthly, Conexus Credit Union has offered 8.34% compounded quarterly, and ING Direct has offered 8.45% compounded semi-annually. Rank the three offers and show calculations to support your answer.
Solution:
Convert all to effective rates to facilitate a fair comparison.
TD Canada Trust:
Step 1: Given information:
[latex]I/Y = 8.3\%[/latex]; [latex]C/Y_{\text{Old}} = 12[/latex]; [latex]C/Y_{\text{New}} = 1[/latex]
Step 2:
[latex]\begin{align} i_{\text{Old}} &= \frac{I/Y}{C/Y_{\text{Old}}}\\ &= \frac{8.3\%}{12}\\ &= 0.691\overline{6}\% \end{align}[/latex]
Step 3:
[latex]\begin{align} i_{\text{New}}&=(1+i_{\text{Old}})^{\frac{C/Y_{\text{Old}}}{C/Y _{\text{New}}}}-1\\ &=(1+0.00691\overline{6})^{\frac{12}{1}}-1\\ &=(1.00691\overline{6})^{12}-1\\ &=1.086231-1\\ &=0.086231 \end{align}[/latex]
8.6231% effectively
CONEXUS Credit Union:
Step 1: Given information:
[latex]I/Y = 8.34\%[/latex]; [latex]C/Y_{\text{Old}} = 4[/latex]; [latex]C/Y_{\text{New}} = 1[/latex]
Step 2:
[latex]\begin{align} i_{\text{Old}} &= \frac{I/Y}{C/Y_{\text{Old}}}\\ & = \frac{8.34\%}{4}\\ &= 2.085\% \end{align}[/latex]
Step 3:
[latex]\begin{align} i_{\text{New}}&=(1+i_{\text{Old}})^{\frac{C/Y_{\text{Old}}}{C/Y _{\text{New}}}}-1\\ &=(1+0.02085)^{\frac{4}{1}}-1\\ &=(1.02085)^{4}-1\\ &=1.086044-1\\ &=0.086045 \end{align}[/latex]
8.6045% effectively
ING Direct:
Step 1: Given information:
[latex]I/Y = 8.45\%[/latex]; [latex]C/Y_{\text{Old}} = 2[/latex]; [latex]C/Y_{\text{New}} = 1[/latex]
Step 2:
[latex]\begin{align} i_{\text{Old}} &= \frac{I/Y}{C/Y_{\text{Old}}}\\ &= \frac{8.45\%}{2}\\ &=4.225\% \end{align}[/latex]
Step 3:
[latex]\begin{align} i_{\text{New}}&=(1+i_{\text{Old}})^{\frac{C/Y_{\text{Old}}}{C/Y _{\text{New}}}}-1\\ &=(1+0.04225)^{\frac{2}{1}}-1 \\ &=(1.04225)^{2}-1\\ &=1.086285-1\\ &=0.086285 \end{align}[/latex]
8.6285% effectively
Ranking:
| Rank | Company | Effective Rate |
|---|---|---|
| 1 | ING Direct | 8.6285% |
| 2 | TD Canada Trust | 8.6231% |
| 3 | CONEXUS Credit Union | 8.6045% |
| Company | NOM | C/Y | EFF |
|---|---|---|---|
| TD | 8.3 | 12 | ? |
| CONEXUS | 8.34 | 4 | ? |
| ING | 8.45 | 2 | ? |
- The TD Emerald Visa card wants to increase its effective rate by 1%. If its current interest rate is 19.067014% compounded daily, what new daily compounded rate should it advertise?
Solution:
First calculate the effective rate.
Step 1: Given information:
[latex]I/Y=19.067014\%[/latex]; [latex]C/Y_{\text{Old}} = 365[/latex]; [latex]C/Y_{\text{New}} = 1[/latex]
Step 2:
[latex]\begin{align} i_{\text{Old}} &= \frac{I/Y}{C/Y_{\text{Old}}}\\ &= \frac{19.067014\%}{365}\\ &=0.052238\% \end{align}[/latex]
Step 3:
[latex]\begin{align} i_{\text{New}}&=(1+i_{\text{Old}})^{\frac{C/Y_{\text{Old}}}{C/Y _{\text{New}}}}-1\\ &=(1+0.00052238)^{\frac{365}{1}}-1\\ &=(1.00052238)^{365}-1\\ &=1.209999-1\\ &=0.21 \end{align}[/latex]
21 % effectively
Now convert it back to a daily rate after making the adjustment (reverse steps 2 & 3):
Step 1:
[latex]i_{\text{New}}=21\%+1\%=22\%[/latex]; [latex]C/Y_{\text{Old}} = 365[/latex]; [latex]C/Y_{\text{New}} = 1[/latex]
Step 3:
[latex]\begin{align} i_{\text{New}}&=(1+i_{\text{Old}})^{\frac{C/Y_{\text{Old}}}{C/Y _{\text{New}}}}-1\\ 0.22&=(1+i_{\text{Old}})^{\frac{365}{1}}-1\\ 1.22&=(1+i_{\text{Old}})^{365}\\ 1.22^{\frac{1}{365}}&=1+i_{\text{Old}}\\ 1.000544&=1+i_{\text{Old}}\\ i_{\text{Old}}&=0.000544 \end{align}[/latex]
Step 2:
[latex]\begin{align} i_{\text{Old}} &= \frac{I/Y}{C/Y_{\text{Old}}}\\ 0.000544&= \frac{I/Y}{365}\\ I/Y&=0.198905 \end{align}[/latex]
19.89% compounded daily
9.7: Determining the Number of Compounds
- You just took over another financial adviser’s account. The client invested $15,500 at 6.92% compounded monthly and now has $24,980.58. How long (in years and months) has this client had the money invested?
Solution:
Step 1: Given information:
[latex]PV=\$15,\!500[/latex]; [latex]I/Y=6.92\%[/latex]; [latex]FV=\$24,\!980.58[/latex]
Step 2: Calculate [latex]i[/latex].
[latex]i=\frac{I/Y}{C/Y}=\frac{6.92\%}{1}=0.57\overline{6}\%[/latex]
Step 3: Use the formula for [latex]FV[/latex], rearrange and solve for [latex]n[/latex].
[latex]\begin{align} FV &= PV(1+i)^n\\ \$24,\!980.58 &= \$15,\!500(1+0.0057\overline{6})^n\\ 1.611650 &= (1.0057\overline{6})^n\\ \ln(1.611650) &= n \times \ln(1.0057\overline{6})\\ 0.477258 &= n \times 0.005750\\ n &= 83 \;\text{monthly compounds} \end{align}[/latex]
[latex]\begin{align} \text{Years} & = \frac{83}{12}= 6.91\overline{6} \;\text{which is}\; 6 \;\text{years plus}\;0.91\overline{6} \times 12 = 11\; \text{months} \end{align}[/latex]
6 years, 11 months
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| ? | 6.92 | 15,500 | 0 | 24,980.58 | 12 | 12 |
- Your organization has a debt of $30,000 due in 13 months and $40,000 due in 27 months. If a single payment of $67,993.20 was made instead using an interest rate of 5.95% compounded monthly, when was the payment made? Use today as the focal date.
Solution:
Step 1: First figure out what the money is worth today.
Original Agreement:
Payment #1 = $30,000 due in 13 months
Payment #2 = $40,000 due in 27 months
[latex]I/Y = 5.95\%[/latex]; [latex]C/Y = 12[/latex]
Proposed Agreement:
$67,993.20 due in x months
Step 2: Focal date = today
Step 3: Calculate [latex]i[/latex].
[latex]i=\frac{I/Y}{C/Y}=\frac{5.95\%}{12}=0.4958\overline{3}\%[/latex]
Step 4: Calculate [latex]n[/latex] of the payments.
Payment #1:
[latex]\begin{align} n &= (\text{Number of Years}) \times (\text{Compounds Per Year})\\ &= 1\frac{1}{12} \times 12\\ &= 1.08\overline{3} \times 12\\ &=13 \end{align}[/latex]
Payment #2:
[latex]\begin{align} n &= (\text{Number of Years}) \times (\text{Compounds Per Year})\\ &= 2\frac{3}{12} \times 12\\ &=2.25 \times 12\\ &= 27 \end{align}[/latex]
Step 5: Calculate [latex]PV[/latex] of the payments.
Payment #1:
[latex]PV = \frac{\$30,\!000}{(1.004958)^{13}} = \$28,\!131.73574[/latex]
Payment #2:
[latex]PV = \frac{\$40,\!000}{(1.004958)^{27}} = \$34,\!999.55193[/latex]
Step 6: Find the total [latex]PV[/latex] of the payments.
[latex]\text{Total today} = \$28,\!131.73574 + \$34,\!999.55193 = \$63,\!131.28768[/latex]
Now figure out where the payment occurs:
Step 1:
[latex]PV=\$63,\!131.28768[/latex]; [latex]FV = \$67,\!993.20[/latex]; [latex]I/Y=5.95\%[/latex]; [latex]C/Y=12[/latex]
Step 2: Find [latex]i[/latex].
[latex]i=\frac{I/Y}{C/Y}=\frac{5.95\%}{12}= 0.4958\overline{3}\%[/latex]
Step 3: Use the formula for [latex]FV[/latex], rearrange and solve for [latex]n[/latex].
[latex]\begin{align} FV &= PV(1+i)^n\\ \$67,\!993.20 &= \$63,\!131.28768(1+0.004958)^n\\ 1.121112 &= (1.004958)^n\\ \ln(1.077012) &= n \times \ln(1.004958)\\ 0.074191 &= n \times 0.004946\\ n &= 15 \;\text{monthly compounds} \end{align}[/latex]
Step 4: Convert the time to years and months.
[latex]\begin{align} \text{Number of years} &= \frac{15}{12}\\ &= 1.25\; \text{which is}\; 1\; \text{year plus}\; 0.25 \times 12 = 3\; \text{months} \end{align}[/latex]
Payment is made 15 months from today.
| Calculation | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Payment 1 | 13 | 5.95 | ? | 0 | 30,000 | 12 | 12 |
| Payment 2 | 27 | 5.95 | ? | 0 | 40,000 | 12 | 12 |
| Timing of Payment | ? | 5.95 | 6,3131.28768 | 0 | 67,993.2 | 12 | 12 |
- A $9,500 loan requires a payment of $5,000 after 1½ years and a final payment of $6,000. If the interest rate on the loan is 6.25% compounded monthly, when should the final payment be made? Use today as the focal date. Express your answer in years and months.
Solution:
Step 1: Given information:
[latex]P=\$9,\!500[/latex]; [latex]I/Y = 6.25\%[/latex]; [latex]C/Y = 12[/latex]
[latex]\text{Payment #}1 = \$5,\!000\; \text{due in}\; 1½\; \text{years}[/latex]
[latex]\text{Payment #}2 = \$6,\!000 \;\text{due in x years}[/latex]
Step 2: Focal date = today
Step 3: Find [latex]i[/latex].
[latex]i=\frac{I/Y}{C/Y}=\frac{6.25\%}{12}= 0.5208\overline{3}\%[/latex]
Step 4: Calculate [latex]n[/latex] for the first payment.
Payment #1:
[latex]\begin{align}n&=(\text{Number of Years}) \times (\text{Compounds Per Year})\\ &= 1\frac{1}{2} \times 12\\ &=1.5 \times 12\\ &= 18 \end{align}[/latex]
Payment #2:
[latex]n = ?[/latex]
Step 5: Calculate [latex]PV[/latex] of the payments.
Payment #1:
[latex]\begin{align} \$5,\!000 &= PV(1+0.005208\overline{3})^{18}\\ PV&=\frac{$5,000}{(1.005208\overline{3})^{18}}\\ &= \$4,\!553.65956 \end{align}[/latex]
Payment #2:
[latex]\begin{align} \$6,\!000 &= PV(1+0.005208\overline{3})^n\\ PV&=\frac{\$6,000}{(1.005208\overline{3})^n} \end{align}[/latex]
Step 6: Solve for [latex]n[/latex] of the final payment.
[latex]\begin{align} \$9,\!500&=\$4,\!553.65956+\frac{\$6,\!000}{(1.005208\overline{3})^n}\\ \$4,\!946.34044&=\frac{\$6,\!000}{(1.005208\overline{3})^n}\\ (1.005208\overline{3})^n&=\frac{\$6,\!000}{\$4,\!946.34044}\\ (1.005208\overline{3})^n&= 1.213018\\ n \times \ln(1.005208) &= \ln(1.213018)\\ n \times 0.005194 &= 0.193111\\ n &= 37.173874\; \text{monthly compounds (round up to}\;38 \; \text{months}) \end{align}[/latex]
Step 7: Convert the time to years and months.
[latex]\begin{align} \text{Number of years} &=\frac{38}{12}\\ &= 3.1\overline{6}\;\text{which is}\;3\;\text{years plus}\;0.1\overline{6} \times 12 = 2 \;\text{months} \end{align}[/latex]
3 years, 2 months
Image Descriptions
Figure 9.2.3: This timeline indicates $9300 at 4.25 years ago. The interest rate of 6.35% compounded semi-annually goes from 4.25 years ago to 1.75 years ago, giving i = 0.03175. The interest rate of 6.5% compounded quarterly goes from 1.75 years ago to today, giving i = 0.01625. $9300 moves from 4.25 years ago to 1.75 years ago as FV1, with n = 2.5 × 2 = 5. FV1 at 1.75 years ago moves to today as FV2 with n = 1.75 × 4 = 7. [Back to Figure 9.2.3]
Figure 9.3.2: This timeline indicates $45,839.05 at 8.5 years. The interest rate of 4.5% compounded semi-annually goes from Loan date to 4.5 years, giving i =4.5%/2 = 0.0225. The interest rate of 3.25% compounded annually goes from 4.5 years to 8.5 years, giving i = 3.25%/1= 0.0325. $9300 moves from 8.5 years to 4.55 years as PV1, with n = 4 × 1 = 4. FV1 at 4.5 years moves to loan date as FV2 with n = 4.5 × 2 = 9. [Back to Figure 9.3.2]
Figure 9.4.1: This timeline shows $250,000 at today, $300,000 at 1 year, $300,000 at 2 years, $300,000 at 3 years. The $300,000 at 1 year moves back to today as PV1, with n = 1 x 1 = 1. The $300,000 at 2 years moves back to today as PV2, with n = 2 x 1 = 2. The $300,000 at 3 years moves back to today as PV3, with n = 3 x 1 = 3. [Back to Figure 9.4.1]
Figure 9.4.2: This is a timeline with debts above the line and payments below the line. The debt of $1600 at 18 months ago is brought to 2 years as FV1 with n = 3.5 x 4 = 14. The debt of $2300 at 9 months ago is brought to 2 years as FV2 with n = 2.75 x 4 = 11. The debt of $5100 at 3 months ago is brought to 2 years as FV3 with n = 2.25 x 4 = 9. The payment of $1000 at today is brought to 2 years as FV4 with n = 2 x 4 = 8. The payment of $4000 at 9 months is brought to 2 years as FV5 with n = 1.25 x 4 = 5. There is a payment of x at 2 years. [Back to Figure 9.4.2]
Figure 9.4.3: This is a timeline with debts above the line and payments below the line. The debt of $7,429.74 at 12 months is brought to 15 months as FV1 with n = (3/12) x 12 = 3. The debt of $3,176.22 at 24 months is brought to 15 months as PV1 with n = (9/12) x 12 = 9. The payment of x at 30 months is brought to 15 months as PV2 with n = (15/12) x 12= 15. There is a payment of 2x at 15 months. [Back to Figure 9.4.3]

