Chapter 13: Solutions to Exercises
13.1: Calculating Interest and Principal Components
- A lump sum of $100,000 is placed into an investment annuity to make end-of-month payments for 20 years at 4% compounded semi-annually.
a) What is the size of the monthly payment?
b) Calculate the principal portion of the 203rd payment.
c) Calculate the interest portion of the 76th payment.
d) Calculate the total interest received in the fifth year.
e) Calculate the principal portion of the payments made in the seventh year.
Solution:
a) What is the size of the monthly payment?
MODE = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 20 \times 12 = 240 \;\text{payments}[/latex]
[latex]I/Y = 4[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = -100,\!000[/latex]
[latex]FV = 0[/latex]
[latex]PV = -100,\!000[/latex]
[latex]CPT\; PMT =\$604.2464648[/latex]
Make sure to reinput PMT =$604.25 (Input as a positive value rounded to 2 decimal places).
b) Calculate the principal portion of the 203rd payment.
2nd AMORT
P1 = 203
P2 = 203
↓
↓
PRN = $533.03
c) Calculate the interest portion of the 76th payment.
2nd AMORT
P1 = 76
P2 = 76
↓
↓
↓
INT = $253.73
d) Calculate the total interest received in the fifth year.
Year 1: payments 1 – 12
Year 2: payments 13 – 24
Year 3: payments 25 – 36
Year 4: payments 37 – 48
Year 5: payments 49 – 60
2nd AMORT
P1 = 49 (Starting with payment 49)
P2 = 60 (Ending with payment 60)
↓
↓
↓
INT = $3,332.61
e) Calculate the principal portion of the payments made in the seventh year.
Year 1: payments 1 – 12
Year 2: payments 13 – 24
Year 3: payments 25 – 36
Year 4: payments 37 – 48
Year 5: payments 49 – 60
Year 6: payments 61 – 72
Year 7: payments 73 – 84
2nd AMORT
P1 = 73
P2 = 84
↓
↓
PRN = $4,241.39
- At the age of 54, Hillary just finished all the arrangements on her parents' estate. She is going to invest her $75,000 inheritance at 6.25% compounded annually until she retires at age 65, and then she wants to receive month-end payments for the following 20 years. The income annuity is expected to earn 3.85% compounded annually.
a) What are the principal and interest portions for the first payment of the income annuity?
b) What is the portion of interest earned on the payments made in the second year of the income annuity?
c) By what amount is the principal of the income annuity reduced in the fifth year?
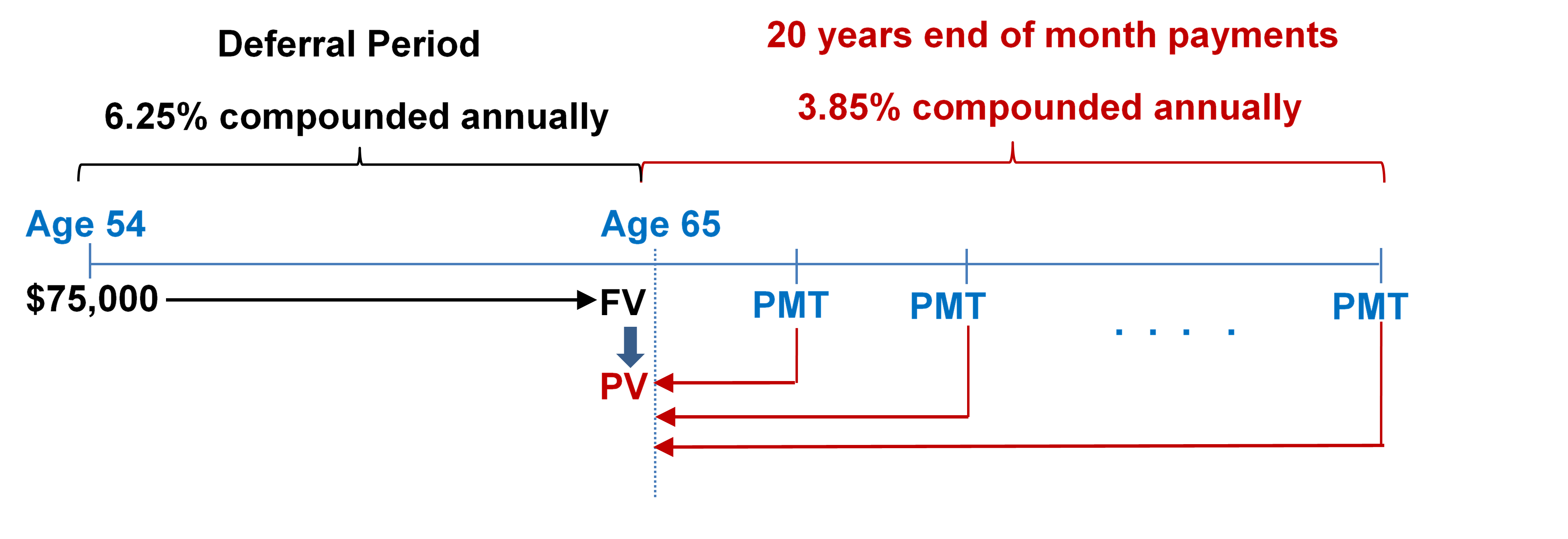
a) What are the principal and interest portions for the first payment of the income annuity?
Step 1: Find [latex]FV[/latex].
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 11 \times 1 = 11 \;\text{payments}[/latex]
[latex]I/Y = 6.25[/latex]
[latex]P/Y = 1[/latex]
[latex]C/Y = 1[/latex]
[latex]PV = 75,\!000[/latex]
[latex]PMT = 0[/latex]
[latex]PV = 75,\!000[/latex]
[latex]CPT\; FV =-\$146,\!109.88[/latex]
Step 2: Find [latex]PMT[/latex].
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 20 \times 12 = 240 \;\text{payments}[/latex]
[latex]I/Y = 3.85[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 1[/latex]
[latex]PV = \$146,\!109.88[/latex]
[latex]FV = 0[/latex]
[latex]PV = \$146,\!109.88[/latex]
[latex]CPT\; PMT =-868.83224[/latex]
Make sure to reinput PMT = -868.83 (Input as a negative value rounded to 2 decimal places).
2nd AMORT
P1 = 1
P2 = 1
↓
↓
PRN = $408.13
INT = $460.70
b) What is the portion of interest earned on the payments made in the second year of the income annuity?
2nd AMORT
P1 = 13
P2 = 24
↓
↓
↓
INT = $5,250.65
c) By what amount is the principal of the income annuity reduced in the fifth year?
2nd AMORT
P1 = 49
P2 = 60
↓
↓
PRN = $5,796.37
- Art Industries just financed a $10,000 purchase at 5.9% compounded annually. It fixes the loan payment at $300 per month.
a) How long will it take to pay the loan off?
b) What are the interest and principal components of the 16th payment?
c) For tax purposes, Art Industries needs to know the total interest paid for payments 7 through 18. Calculate the amount.
Solution:
a) How long will it take to pay the loan off?
Mode = END
[latex]I/Y = 5.9[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 1[/latex]
[latex]PV = 10,\!000[/latex]
[latex]PMT=-300[/latex]
[latex]FV= 0[/latex]
[latex]CPT\; N =36.402469\;\text{rounded up to}\; 37\;\text{ monthly payments}[/latex]
[latex]\begin{align} \text{Number of years}&=\frac{37}{12}\\ &= 3.08\overline{3}\\ &=3\;\text{years and}\; 0.08\overline{3}\times 12=1\; \text{month} \end{align}[/latex]
3 years, 1 month
b) What are the interest and principal components of the 16th payment?
2nd AMORT
P1 = 16
P2 = 16
↓
↓
PRN = $270.84
INT = $29.16
c) For tax purposes, Art Industries needs to know the total interest paid for payments 7 through 18. Calculate the amount.
2nd AMORT
P1 = 7
P2 = 18
↓
↓
↓
INT = $403.33
13.2: Calculating the Final Payment
- Semi-annual payments are to be made against a $97,500 loan at 7.5% compounded semi-annually with a 10-year amortization.
a) What is the amount of the final payment?
b) Calculate the principal and interest portions of the payments in the final two years.
Solution:
a)
Step 1: Find the regular payment.
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 10 \times 2 = 20 \;\text{payments}[/latex]
[latex]I/Y = 7.5[/latex]
[latex]P/Y = 2[/latex]
[latex]C/Y = 2[/latex]
[latex]PV = 97,\!500[/latex]
[latex]FV = 0[/latex]
[latex]CPT\; PMT = -\$7,\!016.30449[/latex]
Make sure to reinput PMT = -7,016.30 (Input as a negative value rounded to 2 decimal places).
Step 2: Use the AMORT function to find the BAL on the last line (payment 20).
2nd AMORT
P1 = 20
P2 = 20
↓
BAL = $0.130277
Step 3: Find the Final Payment
Final Payment = $7,016.30 + $0.130277 = $7,016.43.
b)
Year 9: payments 17-18
Year 10: payments 19-20
2nd AMORT
P1 = 17
P2 = 20
↓
BAL = $0.130277 (*added to payment of $7,016.30 = $7,016.43)
PRN = $25,619.18861 (* add BAL: $25,619.18861 + $0.130277 = $25,619.32)
INT = $2,446.011387
Therefore, PRN = $25,619.32; INT = $2,446.01.
- A $65,000 trust fund is set up to make end-of-year payments for 15 years while earning 3.5% compounded quarterly.
a) What is the amount of the final payment?
b) Calculate the principal and interest portion of the payments in the final three years.
Solution:
a)
Step 1: Find the regular payment.
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 15 \times 1 = 15 \;\text{payments}[/latex]
[latex]I/Y = 3.5[/latex]
[latex]P/Y = 1[/latex]
[latex]C/Y = 4[/latex]
[latex]PV = 65,\!000[/latex]
[latex]FV = 0[/latex]
[latex]CPT\; PMT = -\$5,\!662.190832[/latex]
Make sure to reinput PMT = -5,662.19 (Input as a negative value rounded to 2 decimal places).
Step 2: Use the AMORT function to find the BAL on the last line (payment 15)
2nd AMORT
P1 = 15
P2 = 15
↓
BAL = $0.016114
Step 3: Find the Final Payment
Final Payment = $5,662.19 + $0.016114 = $5,662.21.
b)
2nd AMORT
P1 = 13
P2 = 15
↓
BAL = $0.016114 (*added to payment of $5,662.19 = $5,662.21)
PRN = $15,849.40807 (* add BAL: $15,849.40807 + $0.016114 = $15,849.42)
INT = $1,137.161928
Therefore, PRN = $15,849.42; INT = $1,137.16.
- Mirabel Wholesale has a retail client that is struggling and wants to make instalments against its most recent invoice for $133,465.32. Mirabel works out a plan at 12.5% compounded monthly with beginning-of-month payments for two years.
a) What will be the amount of the final payment?
b) Calculate the principal and interest portions of the payments for the entire agreement.
Solution:
a)
Step 1: Find the regular payment.
Mode = BGN
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 2 \times 12= 24 \;\text{payments}[/latex]
[latex]I/Y = 12.5[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 12[/latex]
[latex]PV = 133,\!465.32[/latex]
[latex]FV = 0[/latex]
[latex]CPT\; PMT = -\$6,\!248.793434[/latex]
Make sure to reinput PMT = -6,248.79 (Input as a negative value rounded to 2 decimal places).
Step 2: Use the AMORT function to find the BAL on the last line (payment 24)
2nd AMORT
P1 = 24
P2 = 24
↓
BAL = $0.093078
Step 3: Find the Final Payment
Final Payment = $6,248.79 + $0.093078 = $6,248.88.
b)
2nd AMORT
P1 = 1
P2 = 24
↓
BAL = $0.093078 (*added to payment of $6,248.79 = $6,248.88)
PRN = $133,465.2269 (* add BAL: $133,465.2269 + $0.093078 = $133,465.32)
INT = $16,505.73308
Therefore, PRN = $133,465.32; INT = $16,505.73.
13.3: Amortization Schedules
- A farmer purchased a John Deere combine for $369,930. The equipment dealership sets up a financing plan to allow for end-of-quarter payments for the next two years at 7.8% compounded monthly. Construct a complete amortization schedule and calculate the total interest.
Solution:
Step 1: Find the regular payment.
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 2 \times 4= 8 \;\text{payments}[/latex]
[latex]I/Y = 7.8[/latex]
[latex]P/Y = 4[/latex]
[latex]C/Y = 12[/latex]
[latex]PV = 369,\!930[/latex]
[latex]FV = 0[/latex]
[latex]CPT\; PMT = -\$50,\!417.92645[/latex]
Make sure to reinput PMT = -50,417.93 (Input as a negative value rounded to 2 decimal places).
Step 2: Use the AMORT function to fill out the table.
| Payment Number | Payment Amount at End of Interval | Interest Accrued During Interval | Principal Paid During Interval | Balance at End of Interval |
|---|---|---|---|---|
| 0 | n/a | n/a | n/a | $369,930.00 |
| 1 | $50,417.93 | $7,260.63 | $43,157.30 | $326,772.70 |
| 2 | $50,417.93 | $6,413.58 | $44,004.35 | $282,768.34 |
| 3 | $50,417.93 | $5,549.90 | $44,868.03 | $237,900.31 |
| 4 | $50,417.93 | $4,669.28 | $45,748.65 | $192,151.66 |
| 5 | $50,417.93 | $3,771.37 | $46,646.56 | $145,505.09 |
| 6 | $50,417.93 | $2,855.83 | $47,562.10 | $97,942.99 |
| 7 | $50,417.93 | $1,922.33 | $48,495.60 | $49,447.39 |
| 8 | $50,417.90 | $970.51 | $49,447.39 | $0.00 |
Step 3: Adjust for the "missing pennies" (noted in bold italics) and total the interest.
| Payment Number | Payment Amount at End of Interval | Interest Accrued During Interval | Principal Paid During Interval | Balance at End of Interval |
|---|---|---|---|---|
| 0 | $369,930.00 | |||
| 1 | $50,417.93 | $7,260.63 | $43,157.30 | $326,772.70 |
| 2 | $50,417.93 | $6,413.57 | $44,004.36 | $282,768.34 |
| 3 | $50,417.93 | $5,549.90 | $44,868.03 | $237,900.31 |
| 4 | $50,417.93 | $4,669.28 | $45,748.65 | $192,151.66 |
| 5 | $50,417.93 | $3,771.36 | $46,646.57 | $145,505.09 |
| 6 | $50,417.93 | $2,855.83 | $47,562.10 | $97,942.99 |
| 7 | $50,417.93 | $1,922.33 | $48,495.60 | $49,447.39 |
| 8 | $50,417.90 | $970.51 | $49,447.39 | $0.00 |
| Total | $403,343.41 | $33,413.41 | $369,930.00 |
- Ron and Natasha had Oasis Leisure and Spa install an in-ground swimming pool for $51,000. The financing plan through the company allows for end-of-month payments for two years at 6.9% compounded quarterly. Ron and Natasha instruct Oasis to round their monthly payment upward to the next dollar amount evenly divisible by $500. Create a schedule for the first three payments, payments seven through nine, and the last three payments.
Solution:
Step 1: Find the regular payment.
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 2 \times 12= 24 \;\text{payments}[/latex]
[latex]I/Y = 6.9[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 4[/latex]
[latex]PV = 51,\!000[/latex]
[latex]FV = 0[/latex]
[latex]CPT\; PMT = -\$2,\!280.18[/latex]
Make sure to reinput PMT = - $2,500 ($2,280.18 rounded up to $2,500).
Step 2: Recalculate N with new PMT.
Mode = END
[latex]I/Y = 6.9[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 4[/latex]
[latex]PV = 51,\!000[/latex]
[latex]PMT = -2,\!500[/latex]
[latex]FV = 0[/latex]
[latex]CPT\; N = 21.753021\; \text{rounded up to}\; 22\; \text{monthly payments}[/latex]
Step 3: Use the AMORT function to fill out the table.
| Payment Number | Payment Amount at End of Interval | Interest Accrued During Interval | Principal Paid During Interval | Balance at End of Interval |
|---|---|---|---|---|
| 0 | $51,000.00 | |||
| 1 | $2,500.00 | $291.58 | $2,208.42 | $48,791.58 |
| 2 | $2,500.00 | $278.95 | $2,221.05 | $46,570.53 |
| 3 | $2,500.00 | $266.26 | $2,233.74 | $44,336.79 |
| ……. | ||||
| $37,558.64 | ||||
| 7 | $2,500.00 | $214.73 | $2,285.27 | $35,273.37 |
| 8 | $2,500.00 | $201.67 | $2,298.33 | $32,975.04 |
| 9 | $2,500.00 | $188.53 | $2,311.47 | $30,663.56 |
| ……… | ||||
| $6,809.38 | ||||
| 20 | $2,500.00 | $38.93 | $2,461.07 | $4,348.31 |
| 21 | $2,500.00 | $24.86 | $2,475.14 | $1,873.17 |
| 22 | $1,883.88 | $10.71 | $1,873.17 | $0.00 |
Step 4: Adjust for the "missing pennies" (noted in bold italics) and total the interest.
| Payment Number | Payment Amount at End of Interval | Interest Accrued During Interval | Principal Paid During Interval | Balance at End of Interval |
|---|---|---|---|---|
| 0 | $51,000.00 | |||
| 1 | $2,500.00 | $291.58 | $2,208.42 | $48,791.58 |
| 2 | $2,500.00 | $278.95 | $2,221.05 | $46,570.53 |
| 3 | $2,500.00 | $266.26 | $2,233.74 | $44,336.79 |
| ……. | ||||
| $37,558.64 | ||||
| 7 | $2,500.00 | $214.73 | $2,285.27 | $35,273.37 |
| 8 | $2,500.00 | $201.67 | $2,298.33 | $32,975.04 |
| 9 | $2,500.00 | $188.52 | $2,311.48 | $30,663.56 |
| ……… | ||||
| $6,809.38 | ||||
| 20 | $2,500.00 | $38.93 | $2,461.07 | $4,348.31 |
| 21 | $2,500.00 | $24.86 | $2,475.14 | $1,873.17 |
| 22 | $1,883.88 | $10.71 | $1,873.17 | $0.00 |
| Total | $21,883.88 | $1,516.21 | $20,367.67 |
- Hillary acquired an antique bedroom set recovered from a European castle for $118,000. She will finance the purchase at 7.95% compounded annually through a plan allowing for payments of $18,000 at the end of every quarter.
a) Create a complete amortization schedule and indicate her total interest paid.
b) Recreate the complete amortization schedule if Hillary pays two additional top-up payments consisting of 10% of the principal remaining after her third payment as well as her fifth payment. What amount of interest does she save?
Solution:
a)
Step 1: Find [latex]N[/latex].
Mode = END
[latex]I/Y = 7.95[/latex]
[latex]P/Y = 4[/latex]
[latex]C/Y = 1[/latex]
[latex]PMT = -18,\!000[/latex]
[latex]PV = 118,\!000[/latex]
[latex]FV = 0[/latex]
[latex]CPT\; N = 7.076614\; \text{rounded up to}\; 8\; \text{quarterly payments}[/latex]
Step 2: Use the AMORT function to fill out the table.
| Payment Number | Payment Amount at End of Interval | Interest Accrued During Interval | Principal Paid During Interval | Balance at End of Interval |
|---|---|---|---|---|
| 0 | $118,000.00 | |||
| 1 | $18,000.00 | $2,278.41 | $15,721.59 | $102,278.41 |
| 2 | $18,000.00 | $1,974.85 | $16,025.15 | $86,253.25 |
| 3 | $18,000.00 | $1,665.42 | $16,334.58 | $69,918.68 |
| 4 | $18,000.00 | $1,350.03 | $16,649.97 | $53,268.71 |
| 5 | $18,000.00 | $1,028.54 | $16,971.46 | $36,297.25 |
| 6 | $18,000.00 | $700.85 | $17,299.15 | $18,998.09 |
| 7 | $18,000.00 | $366.83 | $17,633.17 | $1,364.92 |
| 8 | $1,391.27 | $26.35 | $1,364.92 | $0.00 |
Step 3: Adjust for the "missing pennies" (noted in bold italics) and total the interest.
| Payment Number | Payment Amount at End of Interval | Interest Accrued During Interval | Principal Paid During Interval | Balance at End of Interval |
|---|---|---|---|---|
| 0 | $118,000.00 | |||
| 1 | $18,000.00 | $2,278.41 | $15,721.59 | $102,278.41 |
| 2 | $18,000.00 | $1,974.84 | $16,025.16 | $86,253.25 |
| 3 | $18,000.00 | $1,665.43 | $16,334.57 | $69,918.68 |
| 4 | $18,000.00 | $1,350.03 | $16,649.97 | $53,268.71 |
| 5 | $18,000.00 | $1,028.54 | $16,971.46 | $36,297.25 |
| 6 | $18,000.00 | $700.84 | $17,299.16 | $18,998.09 |
| 7 | $18,000.00 | $366.83 | $17,633.17 | $1,364.92 |
| 8 | $1,391.27 | $26.35 | $1,364.92 | $0.00 |
| Total | $9,391.27 |
b)
Step 1: Use the AMORT function to fill out the table.
| Payment Number | Payment Amount at End of Interval | Interest Accrued During Interval | Principal Paid During Interval | Balance at End of Interval |
|---|---|---|---|---|
| 0 | $0.00 | $118,000.00 | ||
| 1 | $18,000.00 | $2,278.41 | $15,721.59 | $102,278.41 |
| 2 | $18,000.00 | $1,974.85 | $16,025.15 | $86,253.25 |
| 3 | $18,000.00+$6,991.87* =$24,991.87 |
$1,665.42 | $16,334.58+$6,991.87 =$23,326.45 |
$62,926.81 |
| 4 | $18,000.00 | $1,215.02 | $16,784.98 | $46,141.83 |
| 5 | $18,000.00+$2,903.28** =$20,903.28 |
$890.93 | $17,109.07+$2,903.28 =$20,012.35 |
$26,129.48 |
| 6 | $18,000.00 | $504.52 | $17,495.48 | $8,634.01 |
| 7 | $8,800.72 | $166.71 | $8,634.01 | $0.00 |
*The balance after the third payment was $69,918.68. 10% of this amount is $6,991.87.
**The balance after the fifth payment was $29,032.76. 10% of this amount is $2,903.28.
Step 2: Adjust for the "missing pennies" (noted in bold italics) and total the interest.
| Payment Number | Payment Amount at End of Interval | Interest Accrued During Interval | Principal Paid During Interval | Balance at End of Interval |
|---|---|---|---|---|
| 0 | $0.00 | $118,000.00 | ||
| 1 | $18,000.00 | $2,278.41 | $15,721.59 | $102,278.41 |
| 2 | $18,000.00 | $1,974.84 | $16,025.16 | $86,253.25 |
| 3 | $24,991.87 | $1,665.43 | $23,326.44 | $62,926.81 |
| 4 | $18,000.00 | $1,215.02 | $16,784.98 | $46,141.83 |
| 5 | $20,903.28 | $890.93 | $20,012.35 | $26,129.48 |
| 6 | $18,000.00 | $504.53 | $17,495.47 | $8,634.01 |
| 7 | $8,800.72 | $166.71 | $8,634.01 | $0.00 |
| Total | $8,695.87 |
From Question 18a, amount of interest paid was $9,391.27.
Interest Saved = $9,391.27 − $8,695.87 = $695.40.
13.4: Special Application – Mortgages
- Three years ago, Phalatda took out a mortgage on her new home in Kelowna for $628,200 less a $100,000 down payment at 6.49% compounded semi-annually. She is making monthly payments over her three-year term based on a 30-year amortization. At renewal, she is able to obtain a new mortgage on a four-year term at 6.19% compounded semi-annually while continuing with monthly payments and the original amortization timeline.
Calculate the following:
a) Interest and principal portions in the first term.
b) New mortgage payment amount in the second term.
c) Balance remaining after the second term.
Solution:
a)
Step 1: Find the initial payment.
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 30 \times 12 = 360 \;\text{payments}[/latex]
[latex]I/Y = 6.49[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]FV = 0[/latex]
[latex]PV = 628,\!200 − 100,\!000 = 528,\!200[/latex]
[latex]CPT\; PMT =-\$3,\!305.288742[/latex]
Make sure to reinput PMT = -3,305.29 (Input as a negative value rounded to 2 decimal places).
Step 2: Use the AMORT function to find the BAL on the after the first term (payment 1-36).
2nd AMORT
P1 = 1
P2 = 36
↓
BAL = $508,947.54
b)
2nd AMORT
P1 = 1
P2 = 36
↓
↓
PRN = $19,252.46
INT = $99,737.98
c)
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 27 \times 12 = 324 \;\text{payments}[/latex]
[latex]I/Y = 6.19[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]FV = 0[/latex]
[latex]PV = 508,\!947.54[/latex]
[latex]CPT\; PMT =-\$3,\!211.32429[/latex]
Make sure to reinput PMT = -3,211.32 (Input as a negative value rounded to 2 decimal places).
Use the AMORT function to find the BAL on the after the second term (payment 1-48).
2nd AMORT
P1 = 1
P2 = 48
↓
BAL = $475,372.69
- The Verhaeghes have signed a three-year closed fixed rate mortgage with a 20-year amortization and monthly payments. They negotiated an interest rate of 4.84% compounded semi-annually. The terms of the mortgage allow for the Verhaeghes to make a single top-up payment at any one point throughout the term. The mortgage principal was $323,000 and 18 months into the term they made one top-up payment of $20,000.
a)What is the balance remaining at the end of the term?
b)By what amount was the interest portion reduced by making the top-up payment?
Solution:
a)
Step 1: Find the initial payment.
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 20 \times 12 = 240 \;\text{payments}[/latex]
[latex]I/Y = 4.84[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]FV = 0[/latex]
[latex]PV = 323,\!000[/latex]
[latex]CPT\; PMT =-\$2,\!094.701842[/latex]
Make sure to reinput PMT = -2,094.70 (Input as a negative value rounded to 2 decimal places).
Step 2: Use the AMORT function to find the BAL on the after the first 18 months.
2nd AMORT
P1 = 1
P2 = 18
↓
BAL = $308,009.80
Step 3: Find New Balance after $20,000 top-up payment.
New Balance = $308,009.80 − $20,000 = $288,009.80.
Reinput PV = $288,009.80.
Step 4: Use the AMORT function to find the BAL on the after the last 18 months of the first term.
2nd AMORT
P1 = 1
P2 = 18
↓
BAL = $270,417.34
b)
Step 1: Find Original BAL paid without top-up payment (payments 1-36).
Reinput PV = $323,000
2nd AMORT
P1 = 1
P2 = 36
↓
BAL = $291,904.76
Step 2: Find Interest Difference.
[latex]\begin{align} \text{Interest Difference}&=\$291,\!904.76 − \$270,\!417.34 − \$20,\!000\\ &= \$1,\!487.42 \end{align}[/latex]
- Fifteen years ago, Clarissa’s initial principal on her mortgage was $408,650. She set up a 30-year amortization, and in her first 10-year term of monthly payments her mortgage rate was 7.7% compounded semi-annually. Upon renewal, she took a further five-year term with monthly payments at a mortgage rate of 5.69% compounded semi-annually. Today, she renews the mortgage but shortens the amortization period by five years when she sets up a three-year closed fixed rate mortgage of 3.45% compounded semi-annually with monthly payments. What principal will she borrow in her third term and what is the remaining balance at the end of the term? What total interest portion and principal portion will she have paid across all 18 years?
Solution:
Step 1: Find the initial payment for 10-year term.
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 30 \times 12 = 360 \;\text{payments}[/latex]
[latex]I/Y = 7.7[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]FV = 0[/latex]
[latex]PV = 408,\!650[/latex]
[latex]CPT\; PMT =-\$2,\!879.565159[/latex]
Make sure to reinput PMT = -2,879.57 (Input as a negative value rounded to 2 decimal places).
Step 2: Use the AMORT function to find the BAL on the after the 10-year term (payments 1-120).
2nd AMORT
P1 = 1
P2 = 120
↓
BAL = $355,303.81
Step 3: Find the payment for 5-year term.
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 20 \times 12 = 240 \;\text{payments}[/latex]
[latex]I/Y = 5.69[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]FV = 0[/latex]
[latex]PV = 355,\!303.81[/latex]
[latex]CPT\; PMT =-\$2,\!468.979621[/latex]
Make sure to reinput PMT = -2,468.98 (Input as a negative value rounded to 2 decimal places).
Step 4: Use the AMORT function to find the BAL on the after the 5-year term (payments 1-120).
2nd AMORT
P1 = 1
P2 = 60
↓
BAL = $299,756.24
Step 5: Find the payment for 3-year term with amortization period shortened by 5 years. Number of years remaining = 15 – 5 = 10.
Mode = END
[latex]N = (\text{Number of Years}) \times (\text{Payments Per Year})[/latex]
[latex]N = 10 \times 12 = 120 \;\text{payments}[/latex]
[latex]I/Y = 3.45[/latex]
[latex]P/Y = 12[/latex]
[latex]C/Y = 2[/latex]
[latex]FV = 0[/latex]
[latex]PV =299,\!756.24[/latex]
[latex]CPT\; PMT =-\$2,\!953.710318[/latex]
Make sure to reinput PMT = -2,953.71 (Input as a negative value rounded to 2 decimal places).
Step 6: Use the AMORT function to find the BAL on the after the 3-year term (payments 1-36).
2nd AMORT
P1 = 1
P2 = 36
↓
BAL = $220,328.74
Start of 3rd term principal = $299,756.24.
Remaining balance at end of 3rd term = $220,328.74.
[latex]\begin{align} \text{Total principal across all}\;18\;\text{years}&=\$408,\!650 - \$220,\!328.74\\ &= \$188,\!321.26 \end{align}[/latex]
[latex]\text{Total interest across all}\;18\;\text{years}[/latex]
[latex]=(120 \times 2,\!879.57) + (60 \times 2,\!468.98) + (36 \times 2,\!953.71) - 188,\!321.26[/latex]
[latex]= \$411,\!499.50[/latex]
Image Description
Figure 13.1.2: Timeline: Deferral period from age 54 until age 65 at 6.25% compounded annually. Starting at age 55, 20 years end of month payments of PMT at 3.85% compounded annually. $75,000 at age 54 brought to age 65 as FV. At age 65 the FV becomes the PV for the stream of PMT's brought back to age 65. [Back to Figure 13.1.2]

