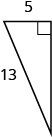Exercises: Use Properties of Angles, Triangles, and the Pythagorean Theorem (6.1)

Exercises: Use the Properties of Angles

Instructions: For questions 1-2, find:

a. the supplement and
b. the complement of the given angle

1. [latex]53^\circ[/latex]

Solution

a. [latex]127^\circ[/latex]
b. [latex]37^\circ[/latex]

2. [latex]29^\circ[/latex]
Solution

a. [latex]151^\circ[/latex]
b. [latex]61^\circ[/latex]

Exercises: Use the Properties of Angles

Instructions: For questions 3-10, use the properties of angles to solve.

3. Find the supplement of a [latex]135^\circ[/latex] angle.

Solution

[latex]45^\circ[/latex]

4. Find the complement of a [latex]38^\circ[/latex] angle.

Solution

[latex]52^\circ[/latex]

5. Find the complement of a [latex]27.5^\circ[/latex] angle.

Solution

[latex]62.5^\circ[/latex]

6. Find the supplement of a [latex]109.5^\circ[/latex] angle.

Solution

[latex]70.5^\circ[/latex]

7. Two angles are supplementary. The larger angle is [latex]56^\circ[/latex] more than the smaller angle. Find the measures of both angles.
Solution

[latex]62^\circ,\;118^\circ[/latex]

8. Two angles are supplementary. The smaller angle is [latex]36^\circ[/latex] less than the larger angle. Find the measures of both angles.

9. Two angles are complementary. The smaller angle is [latex]34^\circ[/latex] less than the larger angle. Find the measures of both angles.

Solution

[latex]62^\circ,\;28^\circ[/latex]

10. Two angles are complementary. The larger angle is [latex]52^\circ[/latex] more than the smaller angle. Find the measures of both angles.

Exercises: Use the Properties of Triangles

Instructions: For questions 11-22, solve using properties of triangles.

11. The measures of two angles of a triangle are [latex]26^\circ[/latex] and [latex]98^\circ[/latex]. Find the measure of the third angle.

Solution

[latex]56^\circ[/latex]

12. The measures of two angles of a triangle are [latex]61^\circ[/latex] and [latex]84^\circ[/latex]. Find the measure of the third angle.

Solution

[latex]35^\circ[/latex]

13. The measures of two angles of a triangle are [latex]105^\circ[/latex] and [latex]31^\circ[/latex]. Find the measure of the third angle.

Solution

[latex]44^\circ[/latex]

14. The measures of two angles of a triangle are [latex]47^\circ[/latex] and [latex]72^\circ[/latex]. Find the measure of the third angle.

Solution

[latex]61^\circ[/latex]

15. One angle of a right triangle measures [latex]33^\circ[/latex]. What is the measure of the other angle?

Solution

[latex]57^\circ[/latex]

16. One angle of a right triangle measures [latex]51^\circ[/latex]. What is the measure of the other angle?

Solution

[latex]39^\circ[/latex]

17. One angle of a right triangle measures [latex]22.5^\circ[/latex]. What is the measure of the other angle?

Solution

[latex]67.5^\circ[/latex]

18. One angle of a right triangle measures [latex]36.5^\circ[/latex]. What is the measure of the other angle?

Solution

[latex]53.5^\circ[/latex]

19. The two smaller angles of a right triangle have equal measures. Find the measures of all three angles.

Solution

[latex]45^\circ,\;45^\circ,\;90^\circ[/latex]

20. The measure of the smallest angle of a right triangle is [latex]20^\circ[/latex] less than the measure of the other small angle. Find the measures of all three angles.

21. The angles in a triangle are such that the measure of one angle is twice the measure of the smallest angle, while the measure of the third angle is three times the measure of the smallest angle. Find the measures of all three angles.

Solution

[latex]30^\circ,\;60^\circ,\;90^\circ[/latex]

22. The angles in a triangle are such that the measure of one angle is [latex]20^\circ[/latex] more than the measure of the smallest angle, while the measure of the third angle is three times the measure of the smallest angle. Find the measures of all three angles.

Exercises: Find the Length of the Missing or Indicated Side

Instructions: For questions 23-24, find the length of the indicated side(s).

23. In the following exercises, [latex]\bigtriangleup ABC[/latex] is similar to [latex]\bigtriangleup XYZ[/latex]. Find the length of the indicated side.

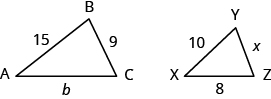
Two triangles are shown. They appear to be the same shape, but the triangle on the right is smaller. The vertices of the triangle on the left are labeled A, B, and C. The side across from A is labeled 9, the side across from B is labeled b, and the side across from C is labeled 15. The vertices of the triangle on the right are labeled X, Y, and Z. The side across from X is labeled x, the side across from Y is labeled 8, and the side across from Z is labeled 10.
Figure 6P.1.1
Solution

Side [latex]b[/latex] = [latex]12[/latex]
Side [latex]x[/latex] = [latex]6[/latex]

24. On a map, San Francisco, Las Vegas, and Los Angeles form a triangle whose sides are shown in the figure below. The actual distance from Los Angeles to Las Vegas is [latex]270[/latex] miles.

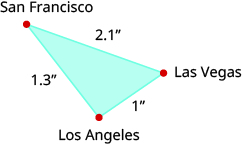
A triangle is shown. The vertices are labeled San Francisco, Las Vegas, and Los Angeles. The side across from San Francisco is labeled 1 inch, the side across from Las Vegas is labeled 1.3 inches, and the side across from Los Angeles is labeled 2.1 inches.
Figure 6P.1.2

a. Find the distance from Los Angeles to San Francisco.
b. Find the distance from San Francisco to Las Vegas.

Solution

a. [latex]351[/latex] miles
b. [latex]567[/latex] miles

Exercises: Use the Pythagorean Theorem

Instructions: For questions 25-28, use the Pythagorean Theorem to find the length of the hypotenuse.

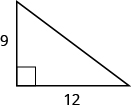
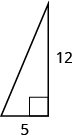
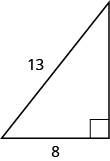
25.

A right triangle is shown. The right angle is marked with a box. One of the sides touching the right angle is labeled as 9, the other as 12.
Figure 6P.1.3
Solution

[latex]15[/latex]

26.
A right triangle is shown. The right angle is marked with a box. One of the sides touching the right angle is labeled as 16, the other as 12.
Figure 6P.1.4
Solution

[latex]20[/latex]

27.
A right triangle is shown. The right angle is marked with a box. One of the sides touching the right angle is labeled as 15, the other as 20.
Figure 6P.1.5
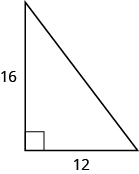
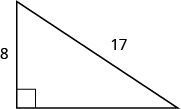
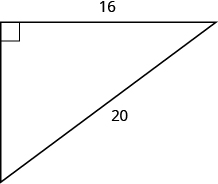
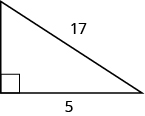
Solution

[latex]25[/latex]

28.

A right triangle is shown. The right angle is marked with a box. One of the sides touching the right angle is labeled as 5, the other as 12.
Figure 6P.1.6
Solution

[latex]13[/latex]

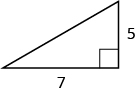
Exercises: Find the Length of the Missing Side

Instructions: For questions 29-36, use the Pythagorean Theorem to find the length of the missing side. Round to the nearest tenth, if necessary.

29.

A right triangle is shown. The right angle is marked with a box. The side across from the right angle is labeled as 10. One of the sides touching the right angle is labeled as 6.
Figure 6P.1.7
Solution

[latex]8[/latex]

30.

A right triangle is shown. The right angle is marked with a box. The side across from the right angle is labeled as 17. One of the sides touching the right angle is labeled as 8.
Figure 6P.1.8
Solution

[latex]15[/latex]

31.

A right triangle is shown. The right angle is marked with a box. The side across from the right angle is labeled as 13. One of the sides touching the right angle is labeled as 5.
Figure 6P.1.9
Solution

[latex]12[/latex]

32.

A right triangle is shown. The right angle is marked with a box. The side across from the right angle is labeled as 20. One of the sides touching the right angle is labeled as 16.
Figure 6P.1.10
Solution

[latex]12[/latex]

33.

A right triangle is shown. The right angle is marked with a box. The side across from the right angle is labeled as 13. One of the sides touching the right angle is labeled as 8.
Figure 6P.1.11
Solution

[latex]10.2[/latex]

34.

A right triangle is shown. The right angle is marked with a box. Both of the sides touching the right angle are labeled as 6.
Figure 6P.1.12
Solution

[latex]8.5[/latex]

35.

A right triangle is shown. The right angle is marked with a box. The side across from the right angle is labeled as 17. One of the sides touching the right angle is labeled as 15.
Figure 6P.1.13
Solution

[latex]8[/latex]

36.

A right triangle is shown. The right angle is marked with a box. The side across from the right angle is labeled as 7. One of the sides touching the right angle is labeled as 5.
Figure 6P.1.14
Solution

[latex]8.6[/latex]

Exercises: Pythagorean Theorem Applications

Instructions: For questions 37-40, solve. Approximate to the nearest tenth, if necessary.

37. A [latex]13 foot[/latex] string of lights will be attached to the top of a [latex]12 foot[/latex] pole for a holiday display. How far from the base of the pole should the end of the string of lights be anchored?

A vertical pole is shown with a string of lights going from the top of the pole to the ground. The pole is labeled 12 feet. The string of lights is labeled 13 feet.
Figure 6P.1.15
Solution

[latex]5[/latex] feet

38. Pam wants to put a banner across her garage door to congratulate her son on his college graduation. The garage door is [latex]12[/latex] feet high and [latex]16[/latex] feet wide. How long should the banner be to fit the garage door?

A picture of a house is shown. The rectangular garage is 12 feet high and 16 feet wide. A blue banner goes diagonally across the garage.
Figure 6P.1.16
Solution

[latex]20[/latex] feet

39. Chi is planning to put a path of paving stones through her flower garden. The flower garden is a square with sides of [latex]10[/latex] feet. What will the length of the path be?

A square garden is shown. One side is labeled as 10 feet. There is a diagonal path of blue circular stones going from the lower left corner to the upper right corner.
Figure 6P.1.17
Solution

[latex]14.1[/latex] feet

40. Brian borrowed a [latex]20 foot[/latex] extension ladder to paint his house. If he sets the base of the ladder [latex]6[/latex] feet from the house, how far up will the top of the ladder reach?

A picture of a house is shown with a ladder leaning against it. The ladder is labeled 20 feet tall. The horizontal distance from the house to the base of the ladder is 6 feet.
Figure 6P.1.18
Solution

[latex]19.1[/latex] feet

Exercises: Everyday Math

Instructions: For questions 41-42, answer the given everyday math word problems.

41. Building a scale model. Joe wants to build a doll house for his daughter. He wants the doll house to look just like his house. His house is [latex]30[/latex] feet wide and [latex]35[/latex] feet tall at the highest point of the roof. If the dollhouse will be [latex]2.5[/latex] feet wide, how tall will its highest point be?
Solution

[latex]2.9 feet[/latex]

42. Measurement A city engineer plans to build a footbridge across a lake from point [latex]X[/latex] to point [latex]Y[/latex], as shown in the picture below. To find the length of the footbridge, she draws a right triangle [latex]\bigtriangleup XYZ[/latex] with right angle at [latex]X[/latex]. She measures the distance from [latex]X[/latex] to [latex]Z[/latex] is [latex]800[/latex] feet, and from [latex]Y[/latex] to [latex]Z[/latex] is [latex]1,000[/latex] feet. How long will the bridge be?

A lake is shown. Point Y is on one side of the lake, directly across from point X. Point Z is on the same side of the lake as point X.
Figure 6P.1.19

Exercises: Writing Exercises

Instructions: For questions 43-44, answer the given writing exercises.

43. Write three of the properties of triangles from this section and then explain each in your own words.
Solution

Answers will vary.

44. Explain how the figure below illustrates the Pythagorean Theorem for a triangle with legs of length [latex]3[/latex] and [latex]4[/latex].

Three squares are shown, forming a right triangle in the center. Each square is divided into smaller squares. The smallest square is divided into 9 small squares. The medium square is divided into 16 small squares. The large square is divided into 25 small squares.
Figure 6P.1.20

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Fanshawe Pre-Health Sciences Mathematics 1 Copyright © 2022 by Domenic Spilotro, MSc is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book