3.10 Slope of a Line

Learning Objectives

By the end of this section, you will be able to:

  • Use [latex]m=\frac{rise}{run}[/latex] to find the slope of a line from its graph
  • Find the slope of horizontal and vertical lines
  • Use the slope formula to find the slope of a line between two points
  • Graph a line given a point and the slope
  • Solve slope applications
  • Recognize the relation between the graph and the slope–intercept form of an equation of a line
  • Identify the slope and [latex]y[/latex]-intercept form of an equation of a line
  • Graph a line using its slope and intercept
  • Choose the most convenient method to graph a line
  • Graph and interpret applications of slope–intercept
  • Use slopes to identify parallel lines
  • Use slopes to identify perpendicular lines

Try It

Before you get started, take this readiness quiz:

1) Simplify: [latex]\frac{1–4}{8-2}[/latex]
2) Divide: [latex]\frac{0}{4},\frac{4}{0}[/latex]
3) Simplify: [latex]\frac{15}{-3},\frac{-15}{3},\frac{-15}{-3}[/latex]
4) Add: [latex]\frac{x}{4}+\frac{1}{4}[/latex]
5) Find the reciprocal of [latex]\frac{3}{7}[/latex]
6) Solve [latex]2x-3y=12[/latex]

When you graph linear equations, you may notice that some lines tilt up as they go from left to right and some lines tilt down. Some lines are very steep and some lines are flatter. What determines whether a line tilts up or down or if it is steep or flat?

In mathematics, the ‘tilt’ of a line is called the slope of the line. The concept of slope has many applications in the real world. The pitch of a roof, grade of a highway, and a ramp for a wheelchair are some examples where you literally see slopes. And when you ride a bicycle, you feel the slope as you pump uphill or coast downhill.

In this section, we will explore the concept of slope.

Use [latex]m=\frac{rise}{run}[/latex] to Find the Slope of a Line from its Graph

Now, we’ll look at some graphs on the [latex]xy[/latex]-coordinate plane and see how to find their slopes. The method we will use here will be similar to how one would use geoboards.

To find the slope, we must count out the rise and the run. But where do we start?

We locate two points on the line whose coordinates are integers. We then start with the point on the left and sketch a right triangle, so we can count the rise and run.

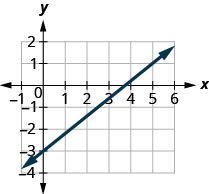
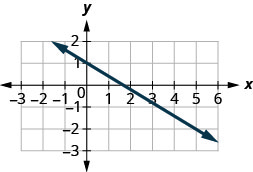
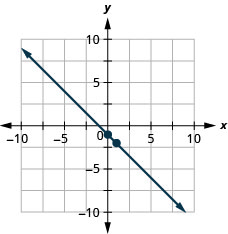
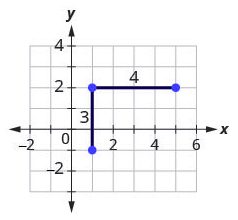
Example 3.10.1

How to Use [latex]m=\frac{rise}{run}[/latex] to Find the Slope of a Line from its Graph

Find the slope of the line shown.

The graph shows the x y coordinate plane. The x-axis runs from negative 1 to 6 and the y-axis runs from negative 4 to 2. A line passes through the points (0, negative 3) and (5, 1).
Figure 3.10.1
Solution
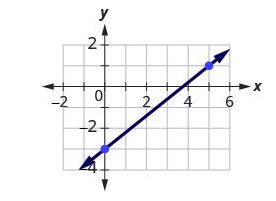
The graph shows the x y coordinate plane. The x-axis runs from negative 1 to 6 and the y-axis runs from negative 4 to 2. A line passes through the points (0, negative 3) and (5, 1).
Figure 3.10.2

Step 1: Locate two points whose coordinates are integers.
Mark [latex](0-,3)(5,1)[/latex]

Step 2: Starting with the point on the left, sketch a right triangle, going from the first point to the second point.

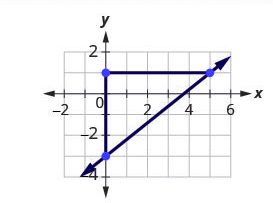
an additional point is plotted at (0, 1). The three points form a right triangle, with the line from (0, negative 3) to (5, 1) forming the hypotenuse and the lines from (0, negative 3) to (0, 1) and (0, 1) to (5, 1) forming the legs.
Figure 3.10.3

Step 3: Count the rise and the run on the legs of the triangle.
Count the rise.
Count the run.

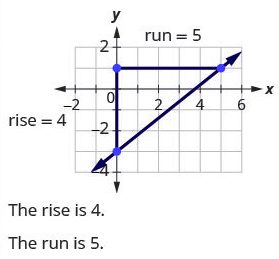
The third row then says, “Step 3: Count the rise and the run on the legs of the triangle.” The rise is 4 and the run is 5.
Figure 3.10.4

Step 4: Take the ration of rise to run to find the slope.

[latex]\begin{align*} &\text{Use the slope formula.}\;&m&=\frac{rise}{run}\\ &\text{Substitute the values of the rise and run.}\;&m&=\frac45\end{align*}[/latex]
The slope of the line is [latex]\frac45[/latex].

Try It

7) Find the slope of the line shown.

The graph shows the x y coordinate plane. The x-axis runs from negative 8 to 1 and the y-axis runs from negative 1 to 4. A line passes through the points (negative 5, 1) and (0, 3).
Figure 3.10.5
Solution

[latex]\frac{2}{5}[/latex]

8) Find the slope of the line shown.

The graph shows the x y coordinate plane. The x-axis runs from negative 1 to 5 and the y-axis runs from negative 2 to 4. A line passes through the points (0, negative 1) and (4, 2).
Figure 3.10.6
Solution

[latex]\frac{3}{4}[/latex]

HOW TO

Find the slope of a line from its graph using [latex]m=\frac{rise}{run}[/latex]

  1. Locate two points on the line whose coordinates are integers.
  2. Starting with the point on the left, sketch a right triangle, going from the first point to the second point.
  3. Count the rise and the run on the legs of the triangle.
  4. Take the ratio of rise to run to find the slope, [latex]m=\frac{rise}{run}[/latex]

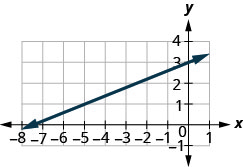
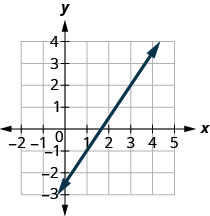
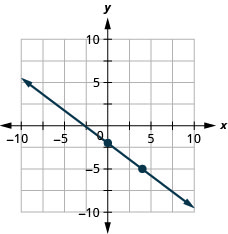
Example 3.10.2

Find the slope of the line shown.

The graph shows the x y coordinate plane. The x-axis runs from negative 1 to 9 and the y-axis runs from negative 1 to 7. A line passes through the points (0, 5), (3, 3), and (6, 1).
Figure 3.10.7
Solution

[latex] m=\frac{rise}{run}[/latex]

Step 1. Locate two points on the graph whose coordinates are integers.

[latex](0,5)[/latex] and [latex](3,3)[/latex]

Step 2: Which point is on the left?

[latex](0,5)[/latex]

Step 3: Starting at [latex](0,5)[/latex], sketch a right triangle to [latex](3,3)[/latex].

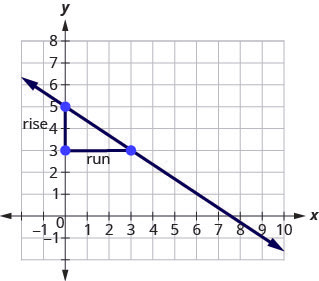
The x-axis of the plane runs from negative 1 to 9. The y-axis of the plane runs from negative 1 to 7. The points (0, 5) and (3, 3) are plotted. An additional point is plotted at (0, 3). The three points form a right triangle, with the line from (0, 5) to (3, 3) forming the hypotenuse and the lines from (0, 5) to (0, 3) and from (0, 3) to (3, 3) forming the legs. The leg from (0, 5) to (0, 3) is labeled “rise” and the leg from (0, 3) to (3, 3) is labeled “run”.
Figure 3.10.8

Step 4: Count the rise—it is negative.

The rise is [latex]-2[/latex].

Step 5: Count the run.

The run is [latex]3[/latex].

Step 6: Use the slope formula.

[latex]m=\frac{rise}{run}[/latex]

Step 7: Substitute the values of the rise and run.

[latex]\begin{align*}&\;&m&=\frac{-2}{3}\\&\text{Simplify.}\;&m&=-\frac{2}{3}\end{align*}[/latex]

The slope of the line is [latex]-\frac{2}{3}[/latex].

The graph shows the x y coordinate plane. The x and y-axes run from negative 7 to 7. A line passes through the points (negative 3, 7) and (6, 1). An additional point is plotted at (negative 3, 1). The three points form a right triangle, with the line from (negative 3, 7) to (6, 1) forming the hypotenuse and the lines from (negative 3, 7) to negative 1, 7) and from (negative 1, 7) to (6, 1) forming the legs.
Figure 3.10.9

So y increases by [latex]3[/latex] units as [latex]x[/latex] decreases by [latex]2[/latex] units. What if we used the points left [latex](-3,7)[/latex] and [latex](6,1)[/latex] to find the slope of the line?The rise would be [latex]-6[/latex] and the run would be [latex]9[/latex]. Then [latex]m=\frac{-6}{9}[/latex], and that simplifies to [latex]m=-\frac{2}{3}[/latex]. Remember, it does not matter which points you use—the slope of the line is always the same.

Try It

9) Find the slope of the line shown.

The graph shows the x y coordinate plane. The x-axis runs from negative 1 to 5 and the y-axis runs from negative 6 to 1. A line passes through the points (0, negative 2) and (3, negative 6).
Figure 3.10.10
Solution

[latex]-\frac{4}{3}[/latex]

10) Find the slope of the line shown.

The graph shows the x y coordinate plane. The x-axis runs from negative 3 to 6 and the y-axis runs from negative 3 to 2. A line passes through the points (0, 1) and (5, negative 2).
Figure 3.10.11
Solution

[latex]-\frac{3}{5}[/latex]

In the last two examples, the lines had [latex]y[/latex]-intercepts with integer values, so it was convenient to use the [latex]y[/latex]-intercept as one of the points to find the slope. In the next example, the [latex]y[/latex]-intercept is a fraction. Instead of using that point, we’ll look for two other points whose coordinates are integers. This will make the slope calculations easier.

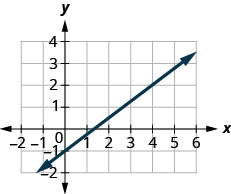
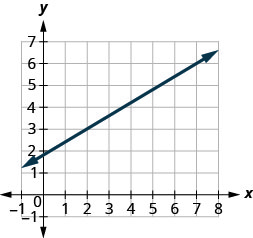
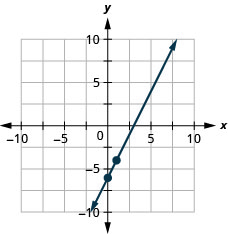
Example 3.10.3

Find the slope of the line shown.
The graph shows the x y coordinate plane. The x-axis runs from 0 to 8 and the y-axis runs from 0 to 7. A line passes through the points (2, 3) and (7, 6).
Figure 3.10.12
Solution

Step 1: Locate two points on the graph whose coordinates are integers.

[latex](2,3)[/latex] and [latex](7,6)[/latex]

Step 2: Which point is on the left?

[latex](2,3)[/latex]

Step 3: Starting at [latex](2,3)[/latex], sketch a right triangle to [latex](7,6)[/latex].

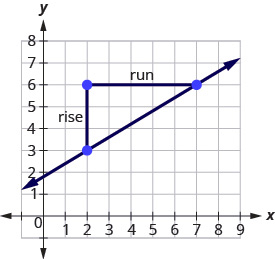
The x-axis of the plane runs from 0 to 8. The y-axis of the plane runs from 0 to 7. The points (2, 3) and (7, 6) are plotted. An additional point is plotted at (2, 6). The three points form a right triangle, with the line from (2, 3) to (7, 6) forming the hypotenuse and the lines from (2, 3) to (2, 6) and from (2, 6) to (7, 6) forming the legs. The leg from (2, 3) to (2, 6) is labeled “rise” and the leg from (2, 6) to (7, 6) is labeled “run”.
Figure 3.10.13

Step 4: Count the rise.

The rise is [latex]3[/latex].

Step 5: Count the run.

The run is [latex]5[/latex].

Step 6: Use the slope formula.

[latex]m=\frac{rise}{run}[/latex]

Step 7: Substitute the values of the rise and run.

The slope of the line is [latex]\frac{3}{5}[/latex]

This means that [latex]y[/latex] increases [latex]5[/latex] units as [latex]x[/latex] increases [latex]3[/latex] units. If you used a geoboard to introduce the concept of slope, you would always start with the point on the left and count the rise and the run to get to the point on the right. That way the run was always positive and the rise determined whether the slope was positive or negative. What would happen if we started with the point on the right? Let’s use the points [latex](2,3)[/latex] and [latex](7,6)[/latex] again, but now we’ll start at [latex](7,6)[/latex].

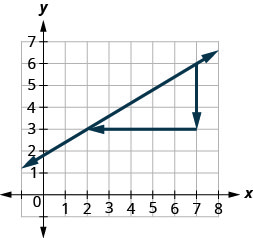
The graph shows the x y coordinate plane. The x -axis runs from 0 to 8. The y -axis runs from 0 to 7. A line passes through the points (2, 3) and (7, 6). An additional point is plotted at (7, 3). The three points form a right triangle, with the line from (2, 3) to (7, 6) forming the hypotenuse and the lines from (2, 3) to (7, 3) and from (7, 3) to (7, 6) forming the legs.
Figure 3.10.14

Step 1: Count the rise.

The rise is [latex]-3[/latex].

Step 2: Count the run. It goes from right to left, so it is negative.

The run is [latex]-5[/latex].

Step 3: Use the slope formula.

[latex]m=\frac{rise}{run}[/latex]

Step 4: Substitute the values of the rise and run.

[latex]m=\frac{-3}{-5}[/latex]

Step 5: The slope of the line is [latex]\frac{3}{5}[/latex].
It does not matter where you start—the slope of the line is always the same.

Try It

11) Find the slope of the line shown.

The graph shows the x y coordinate plane. The x-axis runs from negative 4 to 2 and the y-axis runs from negative 6 to 2. A line passes through the points (negative 3, 4) and (1, 1).
Figure 3.10.15
Solution

[latex]\frac{5}{4}[/latex]

12) Find the slope of the line shown.

The graph shows the x y coordinate plane. The x-axis runs from negative 1 to 4 and the y-axis runs from negative 2 to 3. A line passes through the points (1, negative 1) and (3, 2).
Figure 3.10.16
Solution

[latex]\frac{3}{2}[/latex]

Find the Slope of Horizontal and Vertical Lines

Do you remember what was special about horizontal and vertical lines? Their equations had just one variable.

Horizontal line [latex]y = b[/latex] Vertical line [latex]x = a[/latex]
[latex]y[/latex]-coordinates are the same. [latex]x[/latex]-coordinates are the same.

So how do we find the slope of the horizontal line [latex]y=4[/latex]? One approach would be to graph the horizontal line, find two points on it, and count the rise and the run. Let’s see what happens when we do this.

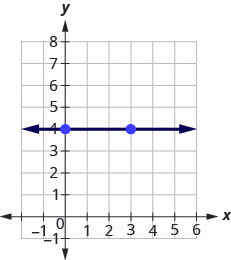
The graph shows the x y coordinate plane. The x-axis runs from negative 1 to 5 and the y-axis runs from negative 1 to 7. A line passes through the points (0, 4) and (3, 4).
Figure 3.10.17

Step 1: What is the rise?

The rise is [latex]0[/latex].

Step 2: Count the run.

The run is [latex]3[/latex].

Step 3: What is the slope?

[latex]\begin{align*}m&=\frac{rise}{run}\\m&=\frac{0}{3}\\m&=0\end{align*}[/latex]

The slope of the horizontal line [latex]y=4[/latex] is [latex]0[/latex].

All horizontal lines have slope [latex]0[/latex]. When the [latex]y[/latex]-coordinates are the same, the rise is [latex]0[/latex].

Slope of a Horizontal Line

The slope of a horizontal line, [latex]y=b[/latex], is [latex]0[/latex].

The floor of your room is horizontal. Its slope is [latex]0[/latex]. If you carefully placed a ball on the floor, it would not roll away.

Now, we’ll consider a vertical line, the line.

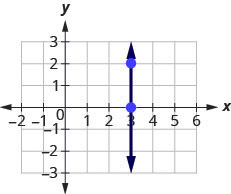
The graph shows the x y coordinate plane. The x-axis runs from negative 1 to 5 and the y-axis runs from negative 2 to 2. A line passes through the points (3, 0) and (3, 2).
Figure 3.10.18

Step 1: What is the rise?

The rise is [latex]2[/latex].

Step 2: Count the run.

The run is [latex]0[/latex].

Step 3: What is the slope?

[latex]\begin{align*}m&=\frac{rise}{run}\\m&=\frac{2}{0}\end{align*}[/latex]

But we can’t divide by [latex]0[/latex]. Division by [latex]0[/latex] is not defined. So we say that the slope of the vertical line [latex]x=3[/latex] is undefined.

The slope of any vertical line is undefined. When the [latex]x[/latex]-coordinates of a line are all the same, the run is [latex]0[/latex].

Slope of a Vertical Line

The slope of a vertical line, [latex]x=a[/latex], is undefined.

Example 3.10.4

Find the slope of each line:

a. [latex]x=8[/latex]
b. [latex]y=-5[/latex]

Solution

a. [latex]x=8[/latex]
 This is a vertical line.
 Its slope is undefined.

b. [latex]y=-5[/latex]
 This is a horizontal line.
 It has slope [latex]0[/latex].

Try It

13) Find the slope of the line: [latex]x=-4[/latex].

Solution

undefined

14) Find the slope of the line: [latex]y=7[/latex].

Solution

[latex]0[/latex]

Quick Guide to the Slopes of Lines

This figure shows four lines with arrows. The first line rises up and runs to the right. It has a positive slope. The second line falls down and runs to the right. It has a negative slope. The third line is neither rises nor falls, extending horizontally in either direction. It has a slope of zero. The fourth line is completely vertical, one end rising up and the other rising down, running neither to the left nor right. It has an undefined slope.
Figure 3.10.19

Remember, we ‘read’ a line from left to right, just like we read written words in English.

Use the Slope Formula to find the Slope of a Line Between Two Points

Sometimes we’ll need to find the slope of a line between two points when we don’t have a graph to count out the rise and the run. We could plot the points on grid paper, then count out the rise and the run, but as we’ll see, there is a way to find the slope without graphing. Before we get to it, we need to introduce some algebraic notation.

We have seen that an ordered pair [latex](x,y)[/latex] gives the coordinates of a point. But when we work with slopes, we use two points. How can the same symbol [latex](x,y)[/latex] be used to represent two different points? Mathematicians use subscripts to distinguish the points.

[latex](x_1,y_1)[/latex] read ‘ [latex]x[/latex] sub 1, [latex]y[/latex] sub 1 ‘
[latex](x_2,y_2)[/latex] read ‘ [latex]x[/latex] sub 2, [latex]y[/latex] sub 2 ‘

The use of subscripts in math is very much like the use of last name initials in elementary school. Maybe you remember Laura C. and Laura M. in your third grade class?

We will use [latex](x_1,y_1)[/latex] to identify the first point and [latex](x_2,y_2)[/latex] to identify the second point.

If we had more than two points, we could use [latex](x_3,y_3)[/latex], [latex](x_4,y_4)[/latex], and so on.

Let’s see how the rise and run relate to the coordinates of the two points by taking another look at the slope of the line between the points [latex](2,3)[/latex] and [latex](7,6)[/latex].

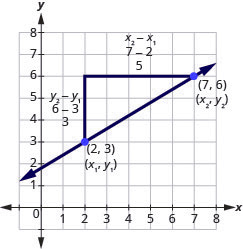
The graph shows the x y coordinate plane. The x and y-axes run from 0 to 7. A line passes through the points (2, 3) and (7, 6), which are plotted and labeled. The ordered pair (2, 3) is labeled (x subscript 1, y subscript 1). The ordered pair (7, 6) is labeled (x subscript 2, y subscript 2). An additional point is plotted at (2, 6). The three points form a right triangle, with the line from (2, 3) to (7, 6) forming the hypotenuse and the lines from (2, 3) to (2, 6) and from (2, 6) to (7, 6) forming the legs. The first leg, from (2, 3) to (2, 6) is labeled y subscript 2 minus y subscript 1, 6 minus 3, and 3. The second leg, from (2, 3) to (7, 6), is labeled x subscript 2 minus x subscript 1, y minus 2, and 5.
Figure 3.10.20

Since we have two points, we will use subscript notation,

[latex]\begin{pmatrix}x_1&y_1\\2&3\end{pmatrix}[/latex]      [latex]\begin{pmatrix}x_2&y_2\\7&6\end{pmatrix}[/latex]

On the graph, we counted the rise of [latex]3[/latex] and the run of [latex]5[/latex].

Notice that the rise of [latex]3[/latex] can be found by subtracting the [latex]y[/latex]-coordinates [latex]6[/latex] and [latex]3[/latex].

[latex]3=6-3[/latex]

And the run of [latex]5[/latex] can be found by subtracting the [latex]x[/latex]-coordinates [latex]7[/latex] and [latex]2[/latex].

[latex]5=7-2[/latex]

We know [latex]m=\frac{rise}{run}[/latex]. So [latex]m=\frac{3}{5}[/latex].

We rewrite the rise and run by putting in the coordinates [latex]m=\frac{6-3}{7-2}[/latex].

But [latex]6[/latex] is [latex]y_2[/latex], the [latex]y[/latex]-coordinate of the second point and [latex]3[/latex] is [latex]y_1[/latex] the [latex]y[/latex]-coordinate of the first point.

So we can rewrite the slope using subscript notation. [latex]m=\frac{y_2-y_1}{7-2}[/latex]

Also, [latex]7[/latex] is [latex]x_2[/latex], the [latex]x[/latex]-coordinate of the second point and [latex]2[/latex] is [latex]x_1[/latex], the [latex]x[/latex]-coordinate of the first point.

So, again, we rewrite the slope using subscript notation. [latex]m=\frac{y_2-y_1}{x_2-x_1}[/latex]

We’ve shown that [latex]m=\frac{y_2-y_1}{x_2-x_1}[/latex] is really another version of [latex]m=\frac{rise}{run}[/latex]. We can use this formula to find the slope of a line when we have two points on the line.

Slope Formula

The slope of the line between two points [latex](x_1,y_1)[/latex] and [latex](x_2,y_2)[/latex] is

[latex]m=\frac{y_2-y_1}{x_2-x_1}[/latex]

This is the slope formula.

The slope is:

[latex]y[/latex] of the second point minus [latex]y[/latex] of the first point
over
[latex]x[/latex] of the second points minus [latex]x[/latex] of the first point

Example 3.10.5

Use the slope formula to find the slope of the line between the points [latex](1,2)[/latex] and [latex](4,5)[/latex].

Solution

[latex]m=\frac{y_2-y_1}{x_2-x_1}[/latex]

Step 1: We’ll call [latex](1,2)[/latex] point #1 and [latex](4,5)[/latex] point #2.

[latex]\begin{pmatrix}x_1&y_1\\1&2\end{pmatrix}[/latex]         [latex]\begin{pmatrix}x_2&y_2\\4&5\end{pmatrix}[/latex]

Step 2: Use the slope formula.

[latex]m=\frac{rise}{run}[/latex]

Step 3: Substitute the values.

[latex]y[/latex] of the second point minus [latex]y[/latex] of the first point.

[latex]m=\frac{5-2}{x_2-x_1}[/latex]

[latex]x[/latex] of the second point minus [latex]x[/latex] of the first point.

[latex]m=\frac{5-2}{4-1}[/latex]

Step 4: Simplify the numerator and the denominator.

[latex]\begin{align*} &\;&m&=\frac33\\ &\text{Simplify.}&m&=1 \end{align*}[/latex]

Let’s confirm this by counting out the slope on a graph using [latex]m=\frac{rise}{run}[/latex].

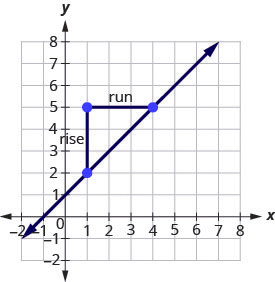
The graph shows the x y-coordinate plane. The x and y-axes of the plane run from 0 to 7. A line passes through the points (1, 2) and (4, 5), which are plotted. An additional point is plotted at (1, 5). The three points form a right triangle, with the line from (1, 2) to (4, 5) forming the hypotenuse and the lines from (1, 2) to (1, 5) and from (1, 5) to (4, 5) forming the legs. The leg from (1, 2) to (1, 5) is labeled “rise” and the leg from (1, 5) to (4, 5) is labeled “run”.
Figure 3.10.21

It doesn’t matter which point you call point #1 and which one you call point #2. The slope will be the same. Try the calculation yourself.

Try It

15) Use the slope formula to find the slope of the line through the points: [latex](8,5)[/latex] and [latex](6,3)[/latex].

Solution

[latex]1[/latex]

16) Use the slope formula to find the slope of the line through the points: [latex](1,5)[/latex] and [latex](5,9)[/latex].

Solution

[latex]1[/latex]

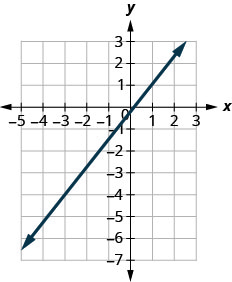
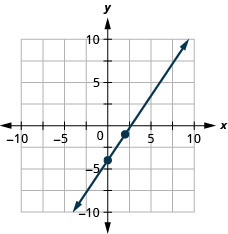
Example 3.10.6

Use the slope formula to find the slope of the line through the points [latex](-2,-3)[/latex] and [latex](-7,4)[/latex].

Solution

Step 1. We’ll call [latex](-2,-3)[/latex] point #1 and [latex](-7,4)[/latex] point #2.

[latex]\begin{pmatrix}x_1&y_1\\-2&-3\end{pmatrix}[/latex]         [latex]\begin{pmatrix}x_2&y_2\\-7&4\end{pmatrix}[/latex]

Step 2. Use the slope formula.

[latex]m=\frac{y_2-y_1}{x_2-x_1}[/latex]

Step 3. Substitute the values.

[latex]y[/latex] of the second point minus [latex]y[/latex] of the first point.

[latex]m=\frac{4-(-3)}{x_2-x_1}[/latex]

[latex]x[/latex] of the second point minus [latex]x[/latex] of the first point.

[latex]m=\frac{4-(-3)}{-7-(-2)}[/latex]

Step 4. Simplify.

[latex]\begin{align*}m&=\frac{7}{-5}\\m&=-\frac{7}{5}\end{align*}[/latex]

Let’s verify this slope on the graph shown.

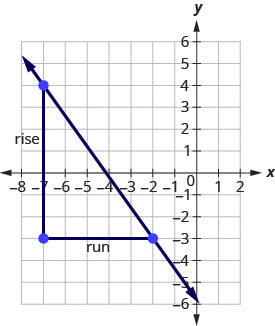
The graph shows the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 2 and the y-axis of the plane runs from negative 6 to 5. A line passes through the points (negative 7, 4) and (negative 2, negative 3), which are plotted and labeled. An additional point is plotted at (negative 7, negative 3). The three points form a right triangle, with the line from (negative 7, 4) to (negative 2, negative 3) forming the hypotenuse and the lines from (negative 7, 4) to (negative 7, negative 3) and from (negative 7, negative 3) to (negative 2, negative 3) forming the legs. The leg from (negative 7, 4) to (negative 7, negative 3) is labeled “rise” and the leg from (negative 7, negative 3) to (negative 2, negative 3) is labeled “run”.
Figure 3.10.22
[latex]\begin{align*}m&=\frac{rise}{run}\\m&=\frac{-7}{5}\\m&=-\frac{7}{5}\end{align*}[/latex]

Try It

17) Use the slope formula to find the slope of the line through the points: [latex](-3,4)[/latex] and [latex](2,-1)[/latex]

Solution

[latex]-1[/latex]

18) Use the slope formula to find the slope of the line through the pair of points: [latex](-2,6)[/latex] and [latex](-3,-4)[/latex].

Solution

[latex]10[/latex]

Graph a Line Given a Point and the Slope

Up to now, in this chapter, we have graphed lines by plotting points, by using intercepts, and by recognizing horizontal and vertical lines.

One other method we can use to graph lines is called the point–slope method. We will use this method when we know one point and the slope of the line. We will start by plotting the point and then use the definition of slope to draw the graph of the line.

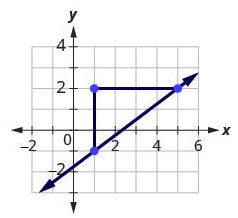
Example 3.10.7

Graph the line passing through the point [latex](1,-1)[/latex] whose slope is [latex]m=\frac{3}{4}[/latex].

Solution

Step 1: Plot the given point.
Plot [latex](1,-1)[/latex].

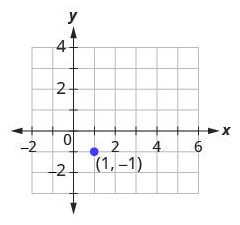
a graph of the x y-coordinate plane. The x-axis of the plane runs from negative 1 to 7. The y-axis of the plane runs from negative 3 to 4. The point (0, negative 1) is plotted.
Figure 3.10.23

Step 2: Use the slope formula [latex]m=\frac{rise}{run}[/latex] to identify the rise and the run.
Identify the rise and the run.

[latex]\begin{align*}m&=\frac34\\[2ex]\frac{rise}{run}&=\frac34\\[3ex]\text{rise}&=3\\\text{run}&=4\end{align*}[/latex]

Step 3: Starting at the given point, count out the rise and run to mark the second point
Start at [latex](1,-1)[/latex] and count the rise and the run. Up [latex]3[/latex] units, right [latex]4[/latex] units.

an additional two points are plotted: (1, 2), which is 3 units up from (1, negative 1), and (5, 2), which is 3 units up and 4 units right from (1, negative 1).
Figure 3.10.24

Step 4: Connect the points with a line.
Connect the two points with a line.

a line is drawn through the points (1, negative 1) and (5, 2). This line is also the hypotenuse of the right triangle formed by the three points, (1, negative 1), (1, 2) and (5, 2).
Figure 3.10.25

Try It

19) Graph the line passing through the point [latex](2,-2)[/latex] with the slope [latex]m=\frac{4}{3}[/latex].

Solution
The graph shows the x y coordinate plane. The x and y-axes run from negative 12 to 12. A line passes through the points (negative 4, negative 10) and (2, negative 2).
Figure 3.10.26

20) Graph the line passing through the point [latex](-2,3)[/latex] with the slope [latex]m=\frac{1}{4}[/latex].

Solution
The graph shows the x y coordinate plane. The x and y-axes run from negative 12 to 12. A line passes through the points (negative 2, 3) and (10, 6).
Figure 3.10.27

HOW TO

Graph a line given a point and the slope.

  1. Plot the given point.
  2. Use the slope formula [latex]m=\frac{rise}{run}[/latex] to identify the rise and the run.
  3. Starting at the given point, count out the rise and run to mark the second point.
  4. Connect the points with a line.

Example 3.10.8

Graph the line with [latex]y[/latex]-intercept [latex]2[/latex] whose slope is [latex]m=-\frac{2}{3}[/latex].
Solution

Step 1: Plot the given point, the [latex]y[/latex]-intercept, [latex](0,2)[/latex].

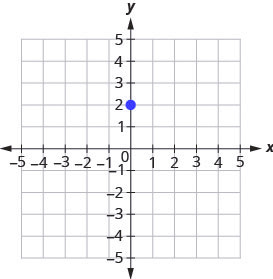
The graph shows the x y coordinate plane. The x and y-axes run from negative 5 to 5. The point (0, 2) is plotted.
Figure 3.10.28

[latex]m=-\frac{2}{3}[/latex]

Step 2: Identify the rise and the run.

[latex]\begin{align*}\left(\frac{rise}{run}\right)&=\frac{-2}{3}\\rise&=-2\\run&=3\end{align*}[/latex]

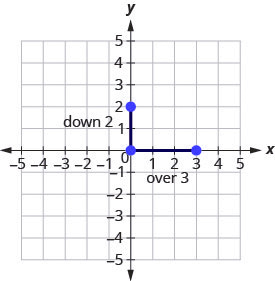
The graph shows the x y coordinate plane. The x and y-axes run from negative 5 to 5. The points (0, 2), (0, 0), and (3,0) are plotted and labeled. The line from (0, 2) to (0, 0) is labeled “down 2” and the line from (0, 0) to (3, 0) is labeled “right 3”.
Figure 3.10.29

Step 3: Count the rise and the run. Mark the second point.

Step 4: Connect the two points with a line.

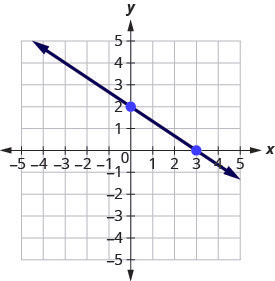
The graph shows the x y coordinate plane. The x and y-axes run from negative 5 to 5. A line passes through the plotted points (0, 2) and (3,0).
Figure 3.10.30

You can check your work by finding a third point. Since the slope is [latex]m=-\frac{2}{3}[/latex], it can be written as [latex]m=\frac{2}{-3}[/latex]. Go back to [latex](0,2)[/latex] and count out the rise, [latex]2[/latex], and the run, [latex]-3[/latex]

Try It

21) Graph the line with the [latex]y[/latex]-intercept [latex]4[/latex] and slope [latex]m=-\frac{5}{2}[/latex].

Solution
The graph shows the x y coordinate plane. The x and y-axes run from negative 12 to 12. A line intercepts the y-axis at (0, 4) and passes through the point (4, negative 6).
Figure 3.10.31

22) Graph the line with the [latex]x[/latex]-intercept [latex]-3[/latex] and slope [latex]m=-\frac{3}{4}[/latex].

Solution
The graph shows the x y coordinate plane. The x and y-axes run from negative 12 to 12. A line intercepts the x-axis at (negative 3, 0) and passes through the point (1, negative 3).
Figure 3.10.32

Example 3.10.9

Graph the line passing through the point [latex](-1,-3)[/latex] whose slope is [latex]m=4[/latex].

Solution

Step 1: Plot the given point.

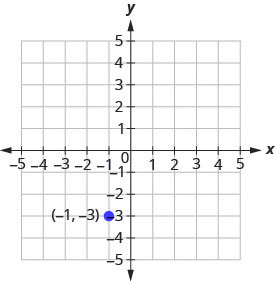
The graph shows the x y coordinate plane. The x and y-axes run from negative 5 to 5. The point (negative 1, negative 3) is plotted and labeled.
Figure 3.10.33

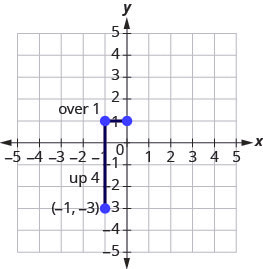
Step 2: Identify the rise and the run.

[latex]m=4[/latex]

Step 3: Write [latex]4[/latex] as a fraction.

[latex]\begin{align*}\frac{rise}{run}&=\frac{4}{1}\\rise&=4\\run&=1\end{align*}[/latex]

Step 4: Count the rise and run and mark the second point.

This figure shows how to graph the line passing through the point (negative 1, negative 3) whose slope is 4. The first step is to identify the rise and run. The rise is 4 and the run is 1. 4 divided by 1 is 4, so the slope is 4. Next we count the rise and run and mark the second point. To the right is a graph of the x y-coordinate plane. The x and y-axes run from negative 5 to 5. We start at the plotted point (negative 1, negative 3) and count the rise, 4. We reach the point negative 1, 1, which we plot. We then count the run from this point, which is 1. We reach the point (0, 1), which is plotted. The last step is to connect the two points with a line. We draw a line which passes through the points (negative 1, negative 3) and (0, 1).
Figure 3.10.34

Step 5: Connect the two points with a line.

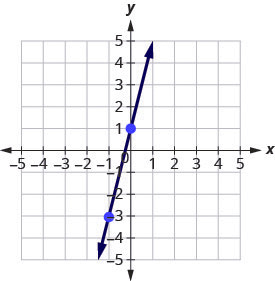
The graph shows the x y coordinate plane. The x and y-axes run from negative 5 to 5. A line passes through the plotted points (-1, -3) and (1,0).
Figure 3.10.35

You can check your work by finding a third point. Since the slope is [latex]m=4[/latex], it can be written as [latex]m=\frac{-4}{-1}[/latex]. Go back to [latex](-1,-3)[/latex] and count out the rise, [latex]-4[/latex], and the run, [latex]-1[/latex].

Try It

23) Graph the line with the point [latex](-2,1)[/latex] and slope [latex]m=3[/latex].

Solution
The graph shows the x y coordinate plane. The x and y-axes run from negative 7 to 7. A line passes through the points (negative 2, 1) and (negative 1, 4).
Figure 3.10.36

24) Graph the line with the point [latex](4,-2)[/latex] and slope [latex]m=-2[/latex].

Solution
The graph shows the x y coordinate plane. The x and y-axes run from negative 7 to 7. A line passes through the points (4, negative 2) and (5, negative 4).
Figure 3.10.37

Solve Slope Applications

At the beginning of this section, we said there are many applications of slope in the real world. Let’s look at a few now.

Example 3.10.10

The ‘pitch’ of a building’s roof is the slope of the roof. Knowing the pitch is important in climates where there is heavy snowfall. If the roof is too flat, the weight of the snow may cause it to collapse. What is the slope of the roof shown?

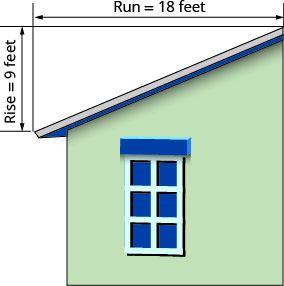
This figure shows a house with a sloped roof. The roof on one half of the building is labeled "pitch of the roof". There is a line segment with arrows at each end measuring the vertical length of the roof and is labeled "rise equals 9 feet". There is a line segment with arrows at each end measuring the horizontal length of the root and is labeled "run equals 18 feet".
Figure 3.10.38
Solution

Step 1: Use the slope formula.

[latex]m=\frac{rise}{run}[/latex]

Step 2: Substitute the values for rise and run.

[latex]m=\frac{9}{18}[/latex]

Step 3: Simplify.

[latex]m=\frac{1}{2}[/latex]

Step 4: The slope of the roof is [latex]\frac{1}{2}[/latex].

The roof rises [latex]1[/latex] foot for every [latex]2[/latex] feet of horizontal run.

Try It

25) Use Example 3.10.10, substituting the [latex]rise = 14[/latex] and [latex]run = 24[/latex].

Solution

[latex]\frac{7}{12}[/latex]

26) Use Example 3.10.10, substituting [latex]rise = 15[/latex] and [latex]run = 36[/latex].

Solution

[latex]\frac{5}{12}[/latex]

Example 3.10.11

Have you ever thought about the sewage pipes going from your house to the street? They must slope down [latex]\frac{1}{4}[/latex] inch per foot in order to drain properly. What is the required slope?

This figure is a right triangle. One leg is negative one quarter inch and the other leg is one foot.
Figure 3.10.39
Solution

Step 1: Use the slope formula

[latex]\begin{align*} &\;&m&=\frac{rise}{run}\\[2ex] &\;&m&=\frac{-\frac14inch}{1\;foot}\\[2ex] &\;&m&=\frac{-\frac14inch}{12\;inches}\\[2ex] &\text{Simplify.}&m&=-\frac1{48} \end{align*}[/latex]

The slope of the pipe is [latex]-\frac{1}{48}[/latex]

The pipe drops [latex]1[/latex] inch for every [latex]48[/latex] inches of horizontal run.

Try It

27) Find the slope of a pipe that slopes down [latex]\frac{1}{3}[/latex] inch per foot.

Solution

[latex]-\frac{1}{36}[/latex]

28) Find the slope of a pipe that slopes down [latex]\frac{3}{4}[/latex] inch per yard.

Solution

[latex]-\frac{1}{48}[/latex]

Recognize the Relation Between the Graph and the Slope–Intercept Form of an Equation of a Line

We have graphed linear equations by plotting points, using intercepts, recognizing horizontal and vertical lines, and using the point–slope method. Once we see how an equation in slope–intercept form and its graph are related, we’ll have one more method we can use to graph lines.

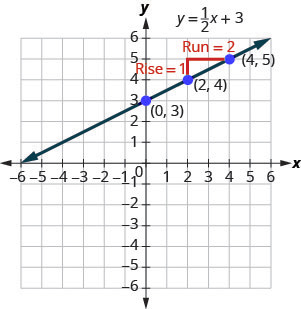
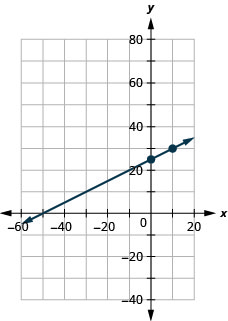
In Graph Linear Equations in Two Variables, we graphed the line of the equation [latex]y=\frac{1}{2}x+3[/latex] by plotting points. See Figure 3.10.40. Let’s find the slope of this line.

 

This figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. The line is labeled with the equation y equals one half x, plus 3. The points (0, 3), (2, 4) and (4, 5) are labeled also. A red vertical line begins at the point (2, 4) and ends one unit above the point. It is labeled “Rise equals 1”. A red horizontal line begins at the end of the vertical line and ends at the point (4, 5). It is labeled “Run equals 2. The red lines create a right triangle with the line y equals one half x, plus 3 as the hypotenuse.
Figure 3.10.40

The red lines show us the rise is [latex]1[/latex] and the run is [latex]2[/latex]. Substituting into the slope formula:

[latex]\begin{align*}m&= \frac {rise}{run}\\m&= \frac {1}{5}\end{align*}[/latex]

What is the [latex]y[/latex]-intercept of the line? The [latex]y[/latex]-intercept is where the line crosses the [latex]y[/latex]-axis, so [latex]y[/latex]-intercept is [latex](0,3)[/latex]. The equation of this line is:

[latex]{y=}{\color{red}{\frac12}}{x+}{\color{blue}{3}}{}[/latex]

Notice, the line has:

Slope [latex]{m=}{\color{red}{\frac12}}[/latex]

When a linear equation is solved for [latex]y[/latex], the coefficient of the [latex]x[/latex] term is the slope and the constant term is the [latex]y[/latex]-coordinate of the [latex]y[/latex]-intercept. We say that the equation [latex]y=\frac{1}{2}x+3[/latex] is in slope–intercept form.

Slope [latex]{m=}{\color{red}{\frac12}}[/latex]

[latex]\begin{align*}y&={\color{red}{\frac12}}x+{\color{blue}{3}}\\y&={\color{red}{m}}x+{\color{blue}{b}}\end{align*}[/latex]

Slope-Intercept Form of an Equation of a Line

The slope–intercept form of an equation of a line with slope [latex]m[/latex] and [latex]y[/latex]-intercept, [latex]\left(0,b\right)[/latex] is,

[latex]y=mx+b[/latex]

Sometimes the slope–intercept form is called the “[latex]y[/latex]-form.”

Example 3.10.12

Use the graph to find the slope and [latex]y[/latex]-intercept of the line, [latex]y=2x+1[/latex].

Compare these values to the equation [latex]y=mx+b[/latex].

Solution
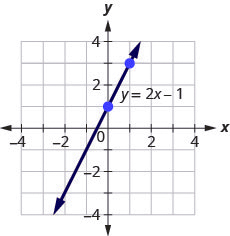
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. The line is labeled with the equation y equals 2 x, plus 1. The points (negative 2, negative 3), (0, 1) and (1, 3) are plotted.
Figure 3.10.41

To find the slope of the line, we need to choose two points on the line. We’ll use the points [latex](0,1)[/latex] and [latex](1,3)[/latex].

Step 1: Find the rise and run.

[latex]\begin{align*}m&=\frac{rise}{run}\\m&=\frac21\\m&=2\end{align*}[/latex]

Step 2: Find the [latex]y[/latex]-intercept of the line.

The [latex]y[/latex]-intercept is the point [latex](0, 1)[/latex].

Step 3: We found the slope [latex]m=2[/latex] and the y-intercept [latex](0,1)[/latex].

[latex]\begin{eqnarray*}y&=&{\color{red}{2}}x\;+\;{\color{blue}{1}}\\y&=&{\color{red}{m}}x\;+\;{\color{blue}{b}}\end{eqnarray*}[/latex]

The slope is the same as the coefficient of [latex]x[/latex] and the [latex]y[/latex]-coordinate of the [latex]y[/latex]-intercept is the same as the constant term.

Try It

29) Use the graph to find the slope and [latex]y[/latex]-intercept of the line [latex]y=\frac{2}{3}x-1[/latex]. Compare these values to the equation [latex]y=mx+b[/latex].

The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. The line goes through the points (0, negative 1) and (6, 3).
Figure 3.10.42
Solution

slope [latex]m=\frac{2}{3}[/latex] and [latex]y[/latex]-intercept [latex](0,-1)[/latex]

30) Use the graph to find the slope and [latex]y[/latex]-intercept of the line [latex]y=\frac{1}{2}x+3[/latex]. Compare these values to the equation [latex]y=mx+b[/latex].

The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. The line goes through the points (0, 3) and (negative 6, 0).
Figure 3.10.43
Solution

slope [latex]m=\frac{1}{2}[/latex] and [latex]y[/latex]-intercept [latex](0,3)[/latex]

Identify the Slope and [latex]y[/latex]-Intercept From an Equation of a Line

In Understand Slope of a Line, we graphed a line using the slope and a point. When we are given an equation in slope–intercept form, we can use the [latex]y[/latex]-intercept as the point, and then count out the slope from there. Let’s practice finding the values of the slope and [latex]y[/latex]-intercept from the equation of a line.

Example 3.10.13

Identify the slope and [latex]y[/latex]-intercept of the line with equation [latex]y=-3x+5[/latex].

Solution

We compare our equation to the slope–intercept form of the equation.

[latex]{y\;=\;}{\color{red}{m}}{x\;+\;}{\color{blue}{b}}[/latex]

Step 1: Write the equation of the line.

[latex]{y=}{\color{red}{-}}{{\color{red}{3}}x\;+\;}{\color{blue}{5}}[/latex]

Step 2: Identify the slope.

[latex]{m=}{\color{red}{-}}{}{\color{red}{3}}[/latex]

Step 3: Identify the [latex]y[/latex]-intercept.

[latex]y[/latex]-intercept is [latex]{\color{black}{(}}{{\color{black}{0}}{\color{black}{,}}{\color{black}{\;}}{\color{blue}{5}}}{\color{black}{)}}[/latex].

Try It

31) Identify the slope and [latex]y[/latex]-intercept of the line [latex]y=\frac{2}{5}x-1[/latex]

Solution

[latex]\frac{2}{5}[/latex]; [latex](0,-1)[/latex]

32) Identify the slope and [latex]y[/latex]-intercept of the line [latex]y=-\frac{4}{3}x+1[/latex]

Solution

[latex]-\frac{4}{3}[/latex]; [latex](0,1)[/latex]

When an equation of a line is not given in slope–intercept form, our first step will be to solve the equation for [latex]y[/latex].

Example 3.10.14

Identify the slope and [latex]y[/latex]-intercept of the line with equation [latex]x+2y=6[/latex].
Solution

This equation is not in slope–intercept form. In order to compare it to the slope–intercept form we must first solve the equation for [latex]y[/latex].

Step 1: Solve for [latex]y[/latex].

[latex]x+2y=6[/latex]

Step 2: Subtract [latex]x[/latex] from each side.

[latex]2y\;=\;-x\;+\;6[/latex]

Step 3: Divide both sides by [latex]2[/latex].

[latex]\begin{align*} &\;&\frac{2y}{2}&=\frac{-x+6}2\\[2ex] &\text{Simplify.}&\frac{2y}2&=\frac{-x}2+\frac62 \end{align*}[/latex]

Remember: [latex]\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}[/latex]

[latex]y\;=-\frac12x\;+\;3[/latex]

Step 6: Write the slope–intercept form of the equation of the line.

[latex]{y\;=\;}{\color{red}{m}}{x\;+\;}{\color{blue}{b}}{}[/latex]

Step 7: Write the equation of the line.

[latex]{y\;=\;-}{\color{red}{\frac12}}{x\;+\;}{\color{blue}{3}}[/latex]

Step 8: Identify the slope.

[latex]{\color{black}{m}}{{\color{black}{\;}}{\color{black}{=}}{\color{blue}{\;}}{\color{red}{-}}}{\color{red}{\frac12}}[/latex]

Step 9: Identify the [latex]y[/latex]-intercept.

[latex]y[/latex]-intercept = [latex]{(0,\;}{\color{blue}{3}}{)}[/latex]

Try It

33) Identify the slope and [latex]y[/latex]-intercept of the line [latex]x+4y=8[/latex].

Solution

[latex]-\frac{1}{4}[/latex]; [latex](0,2)[/latex]

34) Identify the slope and [latex]y[/latex]-intercept of the line [latex]3x+2y=12[/latex].

Solution

[latex]-\frac{3}{2}[/latex]; [latex](0,6)[/latex]

Graph a Line Using its Slope and Intercept

Now that we know how to find the slope and [latex]y[/latex]-intercept of a line from its equation, we can graph the line by plotting the [latex]y[/latex]-intercept and then using the slope to find another point.

Example 3.10.15

 Graph the line of the equation [latex]y=4x-2[/latex] using its slope and [latex]y[/latex]-intercept.

Solution

Step 1: Find the slope-intercept form of the equation.
This equation is in slope-intercept form

[latex]y=4x-2[/latex]

Step 2: Identify the slope and [latex]y[/latex]-intercept.
Use [latex]{y=}{\color{red}{m}}{x+}{\color{blue}{b}}[/latex]
Find the slope.
Find the [latex]y[/latex]-intercept.

[latex]\begin{align*}y&={\color{red}{m}}x+{\color{blue}{b}}\\y&={\color{red}{4}}x+({\color{blue}{-2}})\\m&=4\\b&=-2, (0,-2) \end{align*}[/latex]

Step 3 is to plot the y-intercept. An x y-coordinate plane is shown with the x-axis of the plane running from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. The point (0, negative 2) is plotted.
Figure 3.10.44

Step 4: Use the slope formula [latex]m=\frac{rise}{run}[/latex] to identify the rise and the run.
Identify the rise and the run.

[latex]\begin{align*} m&=4\\ \frac{rise}{run}&=\frac41\\ rise&=4\\ run&=1 \end{align*}[/latex]

Step 5: Starting at the y-intercept, count out the rise and run to mark the second point.
Start at (0,-2) and count the rise and run.
Up 4, right 1.

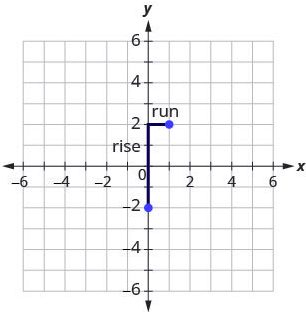
Step 5 is to start at they-intercept, count out the rise and run to mark the second point. So start at the point (0, negative 2) and count the rise and the run. The rise is up 4 and the run is right 1. On the x y-coordinate plane is a red vertical line starts at the point (0, negative 2) and rises 4 units at its end a red horizontal line runs 1 unit to end at the point (1, 2). The point (1, 2) is plotted.
Figure 3.10.45

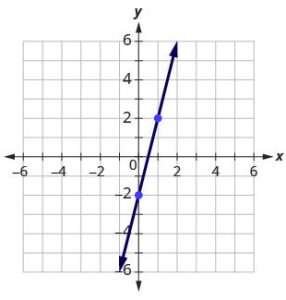
Step 6: Connect the points with a line.
Connect the two points with a line.

On the x y-coordinate plane the points (0, negative 2) and (1, 2) are plotted and a line runs through the two points. The line is the graph of y equals 4 x, minus 2.
Figure 3.10.46

Try It

35) Graph the line of the equation [latex]y=4x+1[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The points (0, 1) and (1, 5) are plotted on the line.
Figure 3.10.47

36) Graph the line of the equation [latex]y=2x-3[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The points (0, negative 3) and (1, negative 1) are plotted on the line.
Figure 3.10.48

HOW TO

Graph a line using its slope and [latex]y[/latex]-intercept.

  1. Find the slope-intercept form of the equation of the line.
  2. Identify the slope and [latex]y[/latex]-intercept.
  3. Plot the [latex]y[/latex]-intercept.
  4. Use the slope formula [latex]m=\frac{rise}{run}[/latex] to identify the rise and the run.
  5. Starting at the [latex]y[/latex]-intercept, count out the rise and run to mark the second point.
  6. Connect the points with a line.

Example 3.10.16

Graph the line of the equation [latex]y=−x+4[/latex] using its slope and [latex]y[/latex]-intercept.

Solution

[latex]y=mx+b[/latex]

Step 1: The equation is in slope–intercept form.

[latex]y=−x+4[/latex]

Step 2: Identify the slope and [latex]y[/latex]-intercept.

[latex]m=-1[/latex]

[latex]y[/latex]-intercept is [latex](0, 4)[/latex]

Step 3: Plot the [latex]y[/latex]-intercept.

See graph below.

Step 4: Identify the rise and the run.

[latex]m=\frac{-1}{1}[/latex]

Step 5: Count out the rise and run to mark the second point.

[latex]rise =−1[/latex], [latex]run=1[/latex]

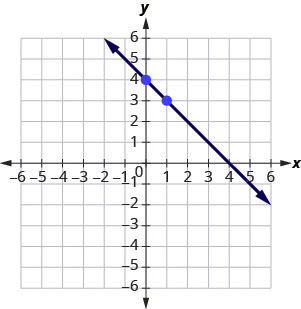
At the very bottom of the figure is a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. The points (0, 4) and (1, 3) are plotted on the line.
Figure 3.10.49

Step 6: Draw the line.

Step 7: To check your work, you can find another point on the line and make sure it is a solution of the equation.

In the graph we see the line goes through [latex](4, 0)[/latex].

Step 8: Check.

[latex]\begin{align*}y&=-x+4\\0&\overset?=-4+4\\0&=0\checkmark\end{align*}[/latex]

Try It

37) Graph the line of the equation [latex]y=−x-3[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The points (0, negative 3) and (1, negative 4) are plotted on the line.
Figure 3.10.50

38) Graph the line of the equation [latex]y=−x-1[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The points (0, negative 1) and (1, negative 2) are plotted on the line.
Figure 3.10.51

Example 3.10.17

Graph the line of the equation [latex]y=-\frac{2}{3}x-3[/latex] using its slope and [latex]y[/latex]-intercept.

Solution

[latex]y=mx+b[/latex]

Step 1: The equation is in slope–intercept form.

[latex]m=-\frac{2}{3}[/latex]; [latex]y[/latex]-intercept is [latex](0, −3)[/latex]

Step 2: Identify the slope and [latex]y[/latex]-intercept.

See graph below.

Step 3: Plot the [latex]y[/latex]-intercept.

Step 4: Identify the rise and the run.

Step 5: Count out the rise and run to mark the second point.

Step 6: Draw the line.

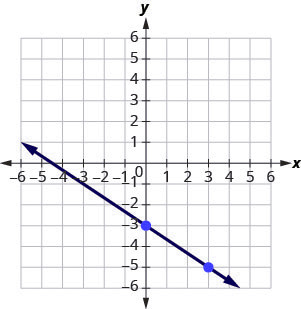
a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. The points (0, negative 3) and (3, negative 5) are plotted on the line.
Figure 3.10.52

Try It

39) Graph the line of the equation [latex]y=-\frac{5}{2}x+1[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The points (0,1) and (2, negative 4) are plotted on the line.
Figure 3.10.53

40) Graph the line of the equation [latex]y=-\frac{3}{4}x-2[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The points (0, negative 2) and (4, negative 5) are plotted on the line.
Figure 3.10.54

Example 3.10.18

Graph the line of the equation [latex]4x-3y=12[/latex] using its slope and [latex]y[/latex]-intercept.

Solution

[latex]4x-3y=12[/latex]

Step 1: Find the slope–intercept form of the equation.

[latex]\begin{align*} 4x-3y&=12\\ -3y&=-4x+12\\ -\frac{3y}{3}&=\frac{-4x+12}{-3} \end{align*}[/latex]

Step 2: The equation is now in slope–intercept form.

[latex]y=\frac{4}{3}x-4[/latex]

Step 3: Identify the slope and [latex]y[/latex]-intercept.

[latex]m=\frac{4}{3}[/latex]

[latex]y[/latex]-intercept is [latex](0, −4)[/latex]

See graph below.

Step 4: Plot the [latex]y[/latex]-intercept.

Step 5: Identify the rise and the run; count out the rise and run to mark the second point.

Step 6: Draw the line.

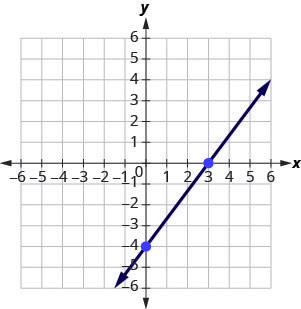
a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. The points (0, negative 4) and (3, 0) are plotted on the line.
Figure 3.10.55

Try It

41) Graph the line of the equation [latex]2x-y=6[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The points (0, negative 6) and (1, negative 4) are plotted on the line.
Figure 3.10.56

42) Graph the line of the equation [latex]3x-2y=8[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The points (0, negative 4) and (2, negative 1) are plotted on the line.
Figure 3.10.57

We have used a grid with [latex]x[/latex] and [latex]y[/latex] both going from about [latex]-10[/latex] to [latex]10[/latex] for all the equations we’ve graphed so far. Not all linear equations can be graphed on this small grid. Often, especially in applications with real-world data, we’ll need to extend the axes to bigger positive or smaller negative numbers.

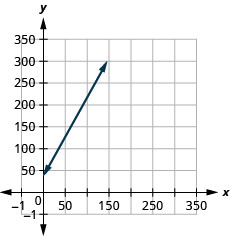
Example 3.10.19

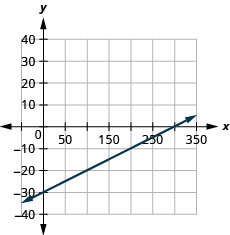
Graph the line of the equation [latex]y=0.2x+45[/latex] using its slope and [latex]y[/latex]-intercept.

Solution

We’ll use a grid with the axes going from about [latex]-80[/latex] to [latex]80[/latex].

[latex]y=mx+b[/latex]

Step 1: The equation is in slope–intercept form.

[latex]y=0.2x+45[/latex]

Step 2: Identify the slope and [latex]y[/latex]-intercept.

[latex]m = 0.2[/latex]

The [latex]y[/latex]-intercept is [latex](0, 45)[/latex].

Step 3: Plot the [latex]y[/latex]-intercept.

See graph below.

Step 4: Count out the rise and run to mark the second point.

The slope is [latex]m = 0.2[/latex]; in fraction form this means [latex]m=\frac{2}{10}[/latex]. Given the scale of our graph, it would be easier to use the equivalent fraction [latex]m=\frac{10}{50}[/latex].

Step 5: Draw the line.

a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 80 to 80. The y-axis of the plane runs from negative 80 to 80. The points (0, 45) and (50, 55) are plotted on the line.
Figure 3.10.58

Try It

43) Graph the line of the equation [latex]y=0.5x+25[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 70 to 30. The y-axis of the plane runs from negative 20 to 40. The points (0, 25) and (10, 30) are plotted on the line.
Figure 3.10.59

44) Graph the line of the equation [latex]y=0.1x-30[/latex] using its slope and [latex]y[/latex]-intercept.

Solution
The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 50 to 350. The y-axis of the plane runs from negative 40 to 40. The points (0, negative 30) and (100, negative 20) are plotted on the line.
Figure 3.10.60
Now that we have graphed lines by using the slope and [latex]y[/latex]-intercept, let’s summarize all the methods we have used to graph lines. See Figure 3.10.61.
The table has two rows and four columns. The first row spans all four columns and is a header row. The header is “Methods to Graph Lines”. The second row is made up of four columns. The first column is labeled “Plotting Points” and shows a smaller table with four rows and two columns. The first row is a header row with the first column labeled “x” and the second labeled “y”. The rest of the table is blank. Below the table it reads “Find three points. Plot the points, make sure they line up, then draw the line.” The Second column is labeled “Slope–Intercept” and shows the equation y equals m x, plus b. Below the equation it reads “Find the slope and y-intercept. Start at the y-intercept, then count the slope to get a second point.” The third column is labeled “Intercepts” and shows a smaller table with four rows and two columns. The first row is a header row with the first column labeled “x” and the second labeled “y”. The second row has a 0 in the “x” column and the “y” column is blank. The second row is blank in the “x” column and has a 0 in the “y” column. The third row is blank. Below the table it reads “Find the intercepts and a third point. Plot the points, make sure they line up, then draw the line.” The fourth column is labeled “Recognize Vertical and Horizontal Lines”. Below that it reads “The equation has only one variable.” The equation x equals a is a vertical line and the equation y equals b is a horizontal line.
Figure 3.10.61

Choose the Most Convenient Method to Graph a Line

Now that we have seen several methods we can use to graph lines, how do we know which method to use for a given equation?

While we could plot points, use the slope–intercept form, or find the intercepts for any equation, if we recognize the most convenient way to graph a certain type of equation, our work will be easier. Generally, plotting points is not the most efficient way to graph a line. We saw better methods in previous sections and earlier in this section. Let’s look for some patterns to help determine the most convenient method to graph a line.

Here are six equations we graphed in this chapter, and the method we used to graph each of them.

Equation Method
#1

[latex]x = 2[/latex]

 Vertical Line
#2 [latex]y = 4[/latex] Horizontal Line
#3 [latex]-x+2y =6[/latex] Intercepts
#4 [latex]4x-3y =12[/latex] Intercepts
#5 [latex]y=4x-2[/latex] Slope-intercept
#6 [latex]y=-x+4[/latex] Slope-intercept

Equations #1 and #2 each have just one variable. Remember, in equations of this form the value of that one variable is constant; it does not depend on the value of the other variable. Equations of this form have graphs that are vertical or horizontal lines.

In equations #3 and #4, both [latex]x[/latex] and [latex]y[/latex] are on the same side of the equation. These two equations are of the form [latex]Ax\;+\;By\;=\;C[/latex]. We substituted [latex]y=0[/latex] to find the [latex]x[/latex]-intercept and [latex]x=0[/latex] to find the [latex]y[/latex]-intercept, and then found a third point by choosing another value for [latex]x[/latex] or [latex]y[/latex].

Equations #5 and #6 are written in slope–intercept form. After identifying the slope and [latex]y[/latex]-intercept from the equation we used them to graph the line.

This leads to the following strategy.

Strategy for Choosing the Most Convenient Method to Graph a Line

Consider the form of the equation.

  • If it only has one variable, it is a vertical or horizontal line.
    • [latex]x=a[/latex] is a vertical line passing through the [latex]x[/latex]-axis at [latex]a[/latex].
    • [latex]y=b[/latex] is a horizontal line passing through the [latex]y[/latex]-axis at [latex]b[/latex].
  • If [latex]y[/latex] is isolated on one side of the equation, in the form [latex]y=mx+b[/latex], graph by using the slope and [latex]y[/latex]-intercept.
    • Identify the slope and [latex]y[/latex]-intercept and then graph.
  • If the equation is of the form [latex]Ax\;+\;By\;=\;C[/latex], find the intercepts.
    • Find the [latex]x[/latex]– and [latex]y[/latex]-intercepts, a third point, and then graph.

Example 3.10.20

Determine the most convenient method to graph each line.

a. [latex]y=-6[/latex]
b. [latex]5x-3y=15[/latex]
c. [latex]x=7[/latex]
d. [latex]y=\frac{2}{5}x-1[/latex]

Solution

a. [latex]y=-6[/latex]
 This equation has only one variable, [latex]y[/latex]. Its graph is a horizontal line crossing the [latex]y[/latex]-axis at [latex]-6[/latex].

b. [latex]5x-3y=15[/latex]
 This equation is of the form [latex]Ax\;+\;By\;=\;C[/latex]. The easiest way to graph it will be to find the intercepts and one more point.

c. [latex]x=7[/latex]
 There is only one variable, [latex]x[/latex]. The graph is a vertical line crossing the [latex]x[/latex]-axis at [latex]7[/latex].

d. [latex]y=\frac{2}{5}x-1[/latex]
 Since this equation is in [latex]y=mx+b[/latex] form, it will be easiest to graph this line by using the slope and [latex]y[/latex]-intercept.

Try It

45) Determine the most convenient method to graph each line:

a. [latex]3x+2y=12[/latex]
b. [latex]y=4[/latex]
c. [latex]y=\frac{1}{5}x-4[/latex]
d. [latex]x=-7[/latex]

Solution

a. intercepts
b. horizontal line
c. slope–intercept
d. vertical line

46) Determine the most convenient method to graph each line:

a. [latex]x=6[/latex]
b. [latex]y=-\frac{3}{4}x+1[/latex]
c. [latex]y=-8[/latex]
d. [latex]4x-3y=-1[/latex]

Solution

a. vertical line
b. slope–intercept
c. horizontal line
d. intercepts

Graph and Interpret Applications of Slope–Intercept

Many real-world applications are modelled by linear equations. We will take a look at a few applications here so you can see how equations written in slope–intercept form relate to real-world situations.

Usually when a linear equation models a real-world situation, different letters are used for the variables, instead of [latex]x[/latex] and [latex]y[/latex]. The variable names remind us of what quantities are being measured.

Example 3.10.21

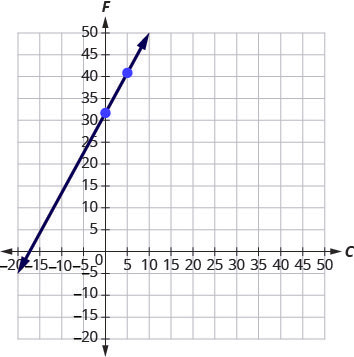
The equation [latex]F=\frac{9}{5}C+32[/latex] is used to convert temperatures, [latex]C[/latex], on the Celsius scale to temperatures, [latex]F[/latex], on the Fahrenheit scale.

a. Find the Fahrenheit temperature for a Celsius temperature of [latex]0[/latex].
b. Find the Fahrenheit temperature for a Celsius temperature of [latex]20[/latex].
c. Interpret the slope and [latex]F[/latex]-intercept of the equation.
d. Graph the equation.

Solution

a.
Step 1: Find the Fahrenheit temperature for a Celsius temperature of [latex]0[/latex].

Step 2: Find [latex]F[/latex] when [latex]C=0[/latex].

[latex]\begin{align*}F&=\frac9 5 C+32\\F&=\frac9 5\times 0+32\\F&= 32\end{align*}[/latex]

b.
Step 1: Find the Fahrenheit temperature for a Celsius temperature of [latex]20[/latex].

Step 2: Find [latex]F[/latex] when [latex]C=20[/latex].

[latex]\begin{align*}F&=\frac9 5 C+32\\F&=\frac9 5 (20)+32\\F&= 36+32\\F&=68\end{align*}[/latex]

c.
Interpret the slope and [latex]F[/latex]-intercept of the equation. Even though this equation uses [latex]F[/latex] and [latex]C[/latex], it is still in slope–intercept form.

[latex]\begin{align*}{\color{red}{y}}&=m{\color{blue}{x}}+b\\{\color{red}{F}}&=m{\color{blue}{C}}+b\\F&=\frac95C+32\end{align*}[/latex]

The slope, [latex]\frac{9}{5}[/latex], means that the temperature Fahrenheit ([latex]F[/latex]) increases [latex]9[/latex] degrees when the temperature Celsius [latex](C)[/latex] increases [latex]5[/latex] degrees. The [latex]F[/latex]-intercept means that when the temperature is [latex](0)[/latex] on the Celsius scale, it is [latex]32^\circ[/latex] on the Fahrenheit scale.

d.
Graph the equation. We’ll need to use a larger scale than our usual. Start at the [latex]F[/latex]-intercept [latex](0,32)[/latex] then count out the rise of [latex]9[/latex] and the run of [latex]5[/latex] to get a second point. See Figure 3.10.62

A graph with 2 points plotted at (0,32) and (5,41)
Figure 3.10.62

Try It

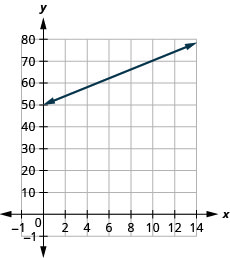
47) The equation [latex]h=2s+50[/latex] is used to estimate a woman’s height in inches, [latex]h[/latex], based on her shoe size, [latex]s[/latex].

a. Estimate the height of a child who wears women’s shoe size [latex]0[/latex].
 b. Estimate the height of a woman with shoe size [latex]8[/latex].
 c. Interpret the slope and [latex]h[/latex]-intercept of the equation.
 d. Graph the equation.

Solution

a. [latex]50[/latex] inches
b. [latex]66[/latex] inches
c. The slope, [latex]2[/latex], means that the height, [latex]h[/latex], increases by [latex]2[/latex] inches when the shoe size, [latex]s[/latex], increases by [latex]1[/latex]. The [latex]h[/latex]-intercept means that when the shoe size is [latex]0[/latex], the height is [latex]50[/latex] inches.
d.

The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane represents the variable s and runs from negative 2 to 15. The y-axis of the plane represents the variable h and runs from negative 1 to 80. The line begins at the point (0, 50) and goes through the points (8, 66).
Figure 3.10.63

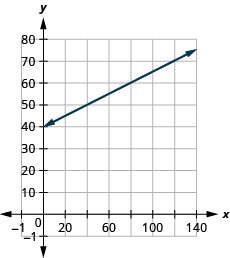
48) The equation [latex]T=\frac{1}{4}n+40[/latex] is used to estimate the temperature in degrees Fahrenheit, [latex]T[/latex], based on the number of cricket chirps, [latex]n[/latex], in one minute.

a. Estimate the temperature when there are no chirps.
 b. Estimate the temperature when the number of chirps in one minute is [latex]100[/latex].
 c. Interpret the slope and [latex]T[/latex]-intercept of the equation.
 d. Graph the equation.

Solution

a. [latex]40[/latex] degrees
b. [latex]65[/latex] degrees
c. The slope, [latex]\frac{1}{4}[/latex], means that the temperature Fahrenheit ([latex]F[/latex]) increases [latex]1[/latex] degree when the number of chirps, [latex]n[/latex], increases by [latex]4[/latex]. The [latex]T[/latex]-intercept means that when the number of chirps is [latex]0[/latex], the temperature is [latex]40^\circ[/latex]

d.

The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane represents the variable n and runs from 10 to 140 The y-axis of the plane represents the variable T and runs from negative 5 to 75. The line begins at the point (0, 40) and goes through the point (100, 65).
Figure 3.10.64

The cost of running some types business has two components—a fixed cost and a variable cost. The fixed cost is always the same regardless of how many units are produced. This is the cost of rent, insurance, equipment, advertising, and other items that must be paid regularly. The variable cost depends on the number of units produced. It is for the material and labour needed to produce each item.

Example 3.10.22

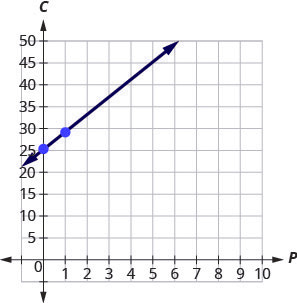
Stella has a home business selling gourmet pizzas. The equation [latex]C=4p+25[/latex] models the relation between her weekly cost, [latex]C[/latex], in dollars and the number of pizzas, [latex]p[/latex], that she sells.

a. Find Stella’s cost for a week when she sells no pizzas.
 b. Find the cost for a week when she sells [latex]15[/latex] pizzas.
 c. Interpret the slope and [latex]C[/latex]-intercept of the equation.
 d. Graph the equation.

Solution

a.

Step 1: Find Stella’s cost for a week when she sells no pizzas.

[latex]C=4p+25[/latex]

Step 2: Find [latex]C[/latex] when [latex]p=0[/latex].

[latex]\begin{align*} &\;&C&=4p+25\\ &\;&C&=4(0)+25\\ &\text{Simplify.}&C&=25 \end{align*}[/latex]

Stella’s fixed cost is [latex]\$25[/latex] when she sells no pizzas.

b.
Step 1: Find the cost for a week when she sells 15 pizzas.

[latex]C=4p+25[/latex]

Step 2: Find [latex]C[/latex] when [latex]p=15[/latex].

[latex]\begin{align*} &\;&C&=4p+25\\ &\;&C&=4(15)+25\\ &\text{Simplify.}&C&=60+25\\ &\;&C&=85 \end{align*}[/latex]

Stella’s costs are [latex]\$85[/latex] when she sells [latex]15[/latex] pizzas.

c.
Step 1: Interpret the slope and [latex]C[/latex]-intercept of the equation.

[latex]\begin{align*} {\color{red}{y}}&=m{\color{blue}{x}}+b\\ {\color{red}{C}}&=4{\color{blue}{p}}+25 \end{align*}[/latex]

The slope, [latex]4[/latex], means that the cost increases by [latex]\$4[/latex] for each pizza Stella sells. The [latex]C[/latex]-intercept means that even when Stella sells no pizzas, her costs for the week are [latex]\$25[/latex].

d.
Step 1: Graph the equation.
We’ll need to use a larger scale than our usual. Start at the [latex]C[/latex]-intercept [latex](0, 25)[/latex] then count out the rise of [latex]4[/latex] and the run of [latex]1[/latex] to get a second point

a line graphed on the x y-coordinate plane. The x-axis of the plane represents the variable p and runs from negative 1 to 20. The y-axis of the plane represents the variable C and runs from negative 1 to 100. The line begins at the point (0, 25) and goes through the point (15, 85).
Figure 3.10.65

Try It

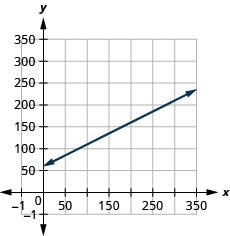
49) Sam drives a delivery van. The equation [latex]C=0.5m+60[/latex] models the relation between his weekly cost, [latex]C[/latex], in dollars and the number of miles, [latex]m[/latex], that he drives.

a. Find Sam’s cost for a week when he drives [latex]0[/latex] miles.
 b. Find the cost for a week when he drives [latex]250[/latex] miles.
 c. Interpret the slope and [latex]C[/latex]-intercept of the equation.
 d. Graph the equation.

Solution

a. [latex]\$60[/latex]
b. [latex]\$185[/latex]
c. The slope, [latex]0.5[/latex], means that the weekly cost, [latex]C[/latex], increases by [latex]\$0.50[/latex] when the number of miles driven, [latex]n[/latex], increases by [latex]1[/latex]. The [latex]C[/latex]-intercept means that when the number of miles driven is [latex]0[/latex], the weekly cost is [latex]\$60[/latex].
d.

The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane represents the variable m and runs from negative 10 to 400. The y-axis of the plane represents the variable C and runs from negative 10 to 300. The line begins at the point (0, 65) and goes through the point (250, 185).
Figure 3.10.66


50) Loreen has a calligraphy business. The equation [latex]C=1.8n+35[/latex] models the relation between her weekly cost, [latex]C[/latex], in dollars and the number of wedding invitations, [latex]n[/latex], that she writes.

a. Find Loreen’s cost for a week when she writes no invitations.
 b. Find the cost for a week when she writes [latex]75[/latex] invitations.
 c. Interpret the slope and [latex]C[/latex]-intercept of the equation.
 d. Graph the equation.

Solution

a. [latex]\$35[/latex]
b. [latex]\$170[/latex]
c. The slope, [latex]1.8[/latex], means that the weekly cost, [latex]C[/latex], increases by [latex]\$1.80[/latex] when the number of invitations, [latex]n[/latex], increases by [latex]1.80[/latex].
 The [latex]C[/latex]-intercept means that when the number of invitations is [latex]0[/latex], the weekly cost is [latex]\$35[/latex].
d.

The figure shows a line graphed on the x y-coordinate plane. The x-axis of the plane represents the variable n and runs from negative 10 to 400. The y-axis of the plane represents the variable C and runs from negative 10 to 300. The line begins at the point (0, 35) and goes through the point (75, 170).
Figure 3.10.67

Use Slopes to Identify Parallel Lines

The slope of a line indicates how steep the line is and whether it rises or falls as we read it from left to right. Two lines that have the same slope are called parallel lines. Parallel lines never intersect.

The figure shows three pairs of lines side-by-side. The pair of lines on the left run diagonally rising from left to right. The pair run side-by-side, not crossing. The pair of lines in the middle run diagonally dropping from left to right. The pair run side-by-side, not crossing. The pair of lines on the right run diagonally also dropping from left to right, but with a lesser slope. The pair run side-by-side, not crossing.
Figure 3.10.68

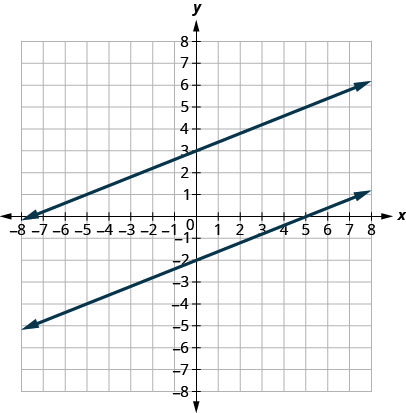
We say this more formally in terms of the rectangular coordinate system. Two lines that have the same slope and different [latex]y[/latex]-intercepts are called parallel lines. See Figure 3.10.69.

Verify that both lines have the same slope, [latex]m=\frac{2}{5}[/latex], and different [latex]y[/latex]-intercepts.
The figure shows two lines graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. One line goes through the points (negative 5,1) and (5,5). The other line goes through the points (negative 5, negative 4) and (5,0).
Figure 3.10.69

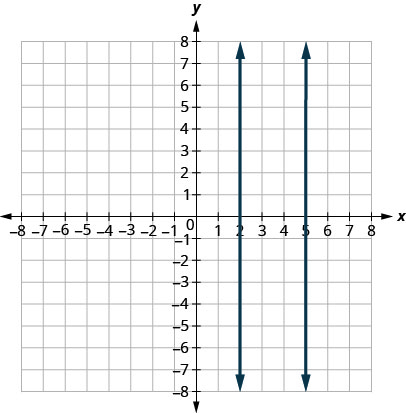
What about vertical lines? The slope of a vertical line is undefined, so vertical lines don’t fit in the definition above. We say that vertical lines that have different [latex]x[/latex]-intercepts are parallel. See Figure 3.10.70.

Vertical lines with different [latex]x[/latex]-intercepts are parallel.

The figure shows two vertical lines graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. One line goes through the points (2,1) and (2,5). The other line goes through the points (5, negative 4) and (5,0).
Figure 3.10.70

Parallel Lines

Parallel lines are lines in the same plane that do not intersect.

  • Parallel lines have the same slope and different [latex]y[/latex]-intercepts.
  • If [latex]m_1[/latex] and [latex]m_2[/latex] are the slopes of two parallel lines then [latex]m_1=m_2[/latex].
  • Parallel vertical lines have different [latex]x[/latex]-intercepts.

Let’s graph the equations [latex]y=-2x+3[/latex] and [latex]2x+y=-1[/latex] on the same grid. The first equation is already in slope–intercept form: [latex]y=-2x+3[/latex]. We solve the second equation for [latex]y[/latex]:

[latex]2x + y = -1[/latex]
[latex]y = -2x-1[/latex]

Graph the lines.

The figure shows two lines graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. One line goes through the points (negative 4, 7) and (3, negative 7). The other line goes through the points (negative 2, 7) and (5, negative 7).
Figure 3.10.71

Notice the lines look parallel. What is the slope of each line? What is the [latex]y[/latex]-intercept of each line?

[latex]y = mx+b[/latex] [latex]y = mx+b[/latex]
[latex]y = -2x +3[/latex] [latex]y = -2x-1[/latex]
[latex]m = -2[/latex] [latex]m = -2[/latex]
[latex]b = 3, (0,3)[/latex] [latex]b = -1, (0,-1)[/latex]

The slopes of the lines are the same and the [latex]y[/latex]-intercept of each line is different. So we know these lines are parallel.

Since parallel lines have the same slope and different [latex]y[/latex]-intercepts, we can now just look at the slope–intercept form of the equations of lines and decide if the lines are parallel.

Example 3.10.23

Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]3x-2y=6[/latex] and [latex]y=\frac{3}{2}x+1[/latex] are parallel.

Solution

Step 1: Solve the first equation for [latex]y[/latex].

[latex]\begin{align*} 3x-2y&=6\\ -2y&=-3x+6\\ \frac{-2y}{-2}&=\frac{3x+6}{-2}\\y&=\frac{3}{2}x-3\end{align*}[/latex] [latex]y=\frac32x+1[/latex]

Step 2: The equation is now in slope-intercept form.

[latex]y=\frac{3}{2}x-3[/latex]

Step 3: The equation of the second line is already in slope-intercept form.

[latex]y=\frac{3}{2}x+1[/latex]

Step 4: Identify the slope and [latex]y[/latex]-intercept of both lines.

[latex]\begin{align*}y&=mx+b\\m&=\frac{3}{2}\\y&= \frac{3}{2}x-3\end{align*}[/latex] [latex]\begin{align*}y&=mx+b\\m&=\frac{3}{2}\\y=\frac{3}{2}x+1\\y&=\frac{3}{2}x+1\end{align*}[/latex]
[latex]y[/latex]-intercept is (0, −3) [latex]y[/latex]-intercept is [latex](0, 1)[/latex]

The lines have the same slope and different [latex]y[/latex]-intercepts and so they are parallel. You may want to graph the lines to confirm whether they are parallel.

Try It

51) Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]2x+5y=5[/latex] and [latex]y=-\frac{2}{5}x-4[/latex] are parallel.

Solution

parallel

52) Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]4x-3y=6[/latex] and [latex]y=\frac{4}{3}x-1[/latex]are parallel.

Solution

parallel

Example 3.10.24

Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]y=-4[/latex] and [latex]y=3[/latex] are parallel.

Solution
[latex]y=-4[/latex] [latex]y=3[/latex]

Step 1: Write each equation in slope-intercept form.
Since there is no [latex]x[/latex] term we write [latex]0x[/latex].

[latex]y=0x-4[/latex] [latex]y=0x+3[/latex]

Step 2: Identify the slope and [latex]y[/latex]-intercept of both lines.

[latex]m=0[/latex] [latex]m=0[/latex]
[latex]y[/latex]-intercept is [latex](0, 4)[/latex] [latex]y[/latex]-intercept is [latex](0, 3)[/latex]

The lines have the same slope and different [latex]y[/latex]-intercepts and so they are parallel.

There is another way you can look at this example. If you recognize right away from the equations that these are horizontal lines, you know their slopes are both [latex]0[/latex]. Since the horizontal lines cross the [latex]y[/latex]-axis at [latex]y=-4[/latex] and at [latex]y=3[/latex], we know the [latex]y[/latex]-intercepts are [latex](0,-4)[/latex] and [latex](0,3)[/latex]. The lines have the same slope and different [latex]y[/latex]-intercepts and so they are parallel.

Try It

53) Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]y=8[/latex] and [latex]y=-6[/latex] are parallel.

Solution

parallel

54) Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]y=1[/latex] and [latex]y=-5[/latex] are parallel.

Solution

parallel

Example 3.10.25

Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]x=-2[/latex] and [latex]x=-5[/latex] are parallel.

Solution
[latex]x=-2[/latex] and [latex]x=-5[/latex]

Since there is no [latex]y[/latex], the equations cannot be put in slope–intercept form. But we recognize them as equations of vertical lines. Their [latex]x[/latex]-intercepts are [latex]-2[/latex] and [latex]-5[/latex]. Since their [latex]x[/latex]-intercepts are different, the vertical lines are parallel.

Try It

55) Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]x=1[/latex] and [latex]x=-5[/latex] are parallel.

Solution

parallel

56) Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]x=8[/latex] and [latex]x=-6[/latex] are parallel.

Solution

parallel

Example 3.10.26

Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]y=2x-3[/latex] and [latex]-6x+3y=-9[/latex] are parallel. You may want to graph these lines, too, to see what they look like.

Solution
[latex]y=2x-3[/latex] [latex]-6x+3y=-9[/latex]

Step 1: The first equation is already in slope-intercept form.

[latex]y=2x-3[/latex]

Step 2: Solve the second equation for [latex]y[/latex].

[latex]\begin{align*} -6x+3y&=-9\\ 3y&=6x-9\\ \frac{3y}{3}&=\frac{6x-9}{3}\\ y&=2x-3 \end{align*}[/latex]

Step 3: The second equation is now in slope-intercept form.

[latex]y=2x-3[/latex] [latex]y=2x-3[/latex]

Step 4: Identify the slope and [latex]y[/latex]-intercept of both lines.

[latex]\begin{align*} y&=2x-3\\ y&=mx+b\\ m&=2 \end{align*}[/latex] [latex]\begin{align*} y&=2x-3\\ y&=mx+b\\ m&=2 \end{align*}[/latex]
[latex]y[/latex]-intercept is [latex](0, −3)[/latex] [latex]y[/latex]-intercept is [latex](0, −3)[/latex]

The lines have the same slope, but they also have the same [latex]y[/latex]-intercepts. Their equations represent the same line. They are not parallel; they are the same line.

Try It

57) Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]y=-\frac{1}{2}x-1[/latex] and [latex]x+2y=2[/latex] are parallel.

Solution

not parallel; same line

58) Use slopes and [latex]y[/latex]-intercepts to determine if the lines [latex]y=\frac{3}{4}x-3[/latex] and [latex]3x-4y=12[/latex] are parallel.

Solution

not parallel; same line

Use Slopes to Identify Perpendicular Lines

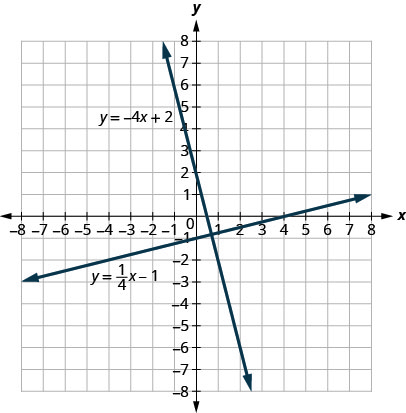
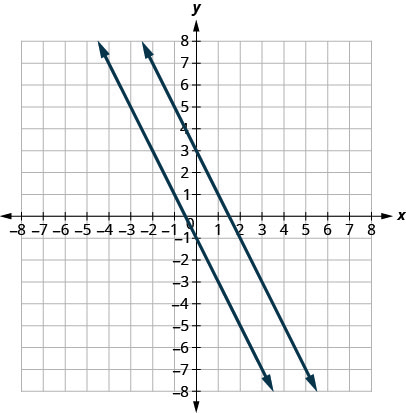
Let’s look at the lines whose equations are [latex]y=\frac{1}{4}x-1[/latex] and [latex]y=-4x+2[/latex], shown in Figure 3.10.72.

The figure shows two lines graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. One line is labeled with the equation y equals negative 4x plus 2 and goes through the points (0,2) and (1, negative 2). The other line is labeled with the equation y equals one fourth x minus 1 and goes through the points (0, negative 1) and (4,0).
Figure 3.10.72

These lines lie in the same plane and intersect in right angles. We call these lines perpendicular.

What do you notice about the slopes of these two lines? As we read from left to right, the line [latex]y=\frac{1}{4}x-1[/latex] rises, so its slope is positive. The line [latex]y=-4x+2[/latex] drops from left to right, so it has a negative slope. Does it make sense to you that the slopes of two perpendicular lines will have opposite signs?

If we look at the slope of the first line, [latex]m_1=\frac{1}{4}[/latex] , and the slope of the second line, [latex]m_2=-4[/latex], we can see that they are negative reciprocals of each other. If we multiply them, their product is [latex]-1[/latex].

[latex]m_1\cdot m_2[/latex]
[latex]\frac{1}{4}(-4)[/latex]
[latex]-1[/latex]

This is always true for perpendicular lines and leads us to this definition.

Perpendicular Lines

Perpendicular lines are lines in the same plane that form a right angle.

If [latex]m_1[/latex] and [latex]m_2[/latex] are the slopes of two perpendicular lines, then:

[latex]m_1\cdot m_2=-1[/latex] and [latex]m_1=-\frac{1}{m_2}[/latex]

Vertical lines and horizontal lines are always perpendicular to each other.

We were able to look at the slope–intercept form of linear equations and determine whether or not the lines were parallel. We can do the same thing for perpendicular lines.

We find the slope–intercept form of the equation, and then see if the slopes are negative reciprocals. If the product of the slopes is [latex]-1[/latex], the lines are perpendicular. Perpendicular lines may have the same [latex]y[/latex]-intercepts.

Example 3.10.27

Use slopes to determine if the lines, [latex]y=-5x-4[/latex] and [latex]x-5y=5[/latex] are perpendicular.

Solution

Step 1: The first equation is already in slope-intercept form.

[latex]y=-5x-4[/latex]

Step 2: Solve the second equation for [latex]y[/latex].

[latex]\begin{align*} x-5y&=5\\ -5y&=x+5\\ \frac{-5y}{-5}&=\frac{x+5}{-5}\\ y&=\frac{1}{-5}x-1 \end{align*}[/latex]

Step 3: Identify the slope of each line.

[latex]\begin{align*} y&=-5x-4\\ y&=mx+b\\ m_1&=-5 \end{align*}[/latex] [latex]\begin{align*} y&=\frac{1}{5}x-4\\ y&=mx+b\\ m_2&=\frac{1}{5} \end{align*}[/latex]

The slopes are negative reciprocals of each other, so the lines are perpendicular. We check by multiplying the slopes,

[latex]\begin{align*}m_1\cdot m_2\\&=-5(\frac{1}{5})\\&=-1\end{align*}[/latex]

Try It

59) Use slopes to determine if the lines [latex]y=-3x+2[/latex] and [latex]x-3y=4[/latex] are perpendicular.

Solution

perpendicular

60) Use slopes to determine if the lines [latex]y=2x-5[/latex] and [latex]x+2y=-6[/latex] are perpendicular.

Solution

perpendicular

Example 3.10.28

Use slopes to determine if the lines, [latex]7x+2y=3[/latex] and [latex]2x+7y=5[/latex] are perpendicular.

Solution

Step 1: Solve the equations for [latex]y[/latex].

[latex]\begin{align*} 7x+2y&=3\\ 2y&=-7x+3\\ \frac{2y}{2}&=\frac{-7x+3}{2}\\ y&=\frac{-7}{2}x+\frac{3}{2} \end{align*}[/latex] [latex]\begin{align*} 2x+7y&=5\\ 2y&=-2x+5\\ \frac{7y}{7}&=\frac{-2x+5}{7}\\ y&=\frac{-2}{7}x+\frac{5}{7} \end{align*}[/latex]

Step 2: Identify the slope of each line.

[latex]\begin{align*}y&=mx+b\\m_1&=-\frac{7}{2}\end{align*}[/latex] [latex]\begin{align*}y&=mx+b\\m_2&=-\frac{2}{7}\end{align*}[/latex]

The slopes are reciprocals of each other, but they have the same sign. Since they are not negative reciprocals, the lines are not perpendicular.

Try It

61) Use slopes to determine if the lines [latex]5x+4y=1[/latex] and [latex]4x+5y=3[/latex] are perpendicular.

Solution

not perpendicular

62) Use slopes to determine if the lines [latex]2x-9y=3[/latex] and [latex]9x-2y=1[/latex] are perpendicular.

Solution

not perpendicular

Key Concepts

  • Find the Slope of a Line from its Graph using [latex]m=\frac{rise}{run}[/latex]
  1. Locate two points on the line whose coordinates are integers.
  2. Starting with the point on the left, sketch a right triangle, going from the first point to the second point.
  3. Count the rise and the run on the legs of the triangle.
  4. Take the ratio of rise to run to find the slope.
  • Graph a Line Given a Point and the Slope
  1. Plot the given point.
  2. Use the slope formula [latex]m=\frac{rise}{run}[/latex] to identify the rise and the run.
  3. Starting at the given point, count out the rise and run to mark the second point.
  4. Connect the points with a line.
  • Slope of a Horizontal Line
    • The slope of a horizontal line, [latex]y=b[/latex], is [latex]0[/latex].
  • Slope of a vertical line
    • The slope of a vertical line, [latex]x=a[/latex], is undefined

Graph a Line Using its Slope and y-Intercept

  1. The slope–intercept form of an equation of a line with slope [latex]m[/latex] and [latex]y[/latex]-intercept, [latex](0,b)[/latex] is, [latex]y=mx+b[/latex].
  2. Find the slope-intercept form of the equation of the line.
  3. Identify the slope and [latex]y[/latex]-intercept.
  4. Plot the [latex]y[/latex]-intercept.
  5. Use the slope formula [latex]m=\frac{rise}{run}[/latex] to identify the rise and the run.
  6. Starting at the [latex]y[/latex]-intercept, count out the rise and run to mark the second point.
  7. Connect the points with a line.
  •  Strategy for Choosing the Most Convenient Method to Graph a Line: Consider the form of the equation.
    • If it only has one variable, it is a vertical or horizontal line.
      [latex]x=a[/latex] is a vertical line passing through the [latex]x[/latex]-axis at [latex]a[/latex].
      [latex]y=b[/latex] is a horizontal line passing through the [latex]y[/latex]-axis at [latex]b[/latex].
    • If [latex]y[/latex] is isolated on one side of the equation, in the form [latex]y=mx+b[/latex], graph by using the slope and [latex]y[/latex]-intercept.
       Identify the slope and [latex]y[/latex]-intercept and then graph.
    • If the equation is of the form [latex]Ax\;+\;By\;=\;C[/latex], find the intercepts.
       Find the [latex]x[/latex]-intercept and [latex]y[/latex]-intercept, a third point, and then graph.
  • Parallel lines are lines in the same plane that do not intersect.
    • Parallel lines have the same slope and different [latex]y[/latex]-intercepts.
      • If [latex]m_1[/latex] and [latex]m_2[/latex] are the slopes of two parallel lines then [latex]m_1=m_2[/latex].
    • Parallel vertical lines have different [latex]x[/latex]-intercepts.
  • Perpendicular lines are lines in the same plane that form a right angle.
    • If [latex]m_1[/latex] and [latex]m_2[/latex] are the slopes of two perpendicular lines, then [latex]m_1\cdot m_2=-1[/latex] and [latex]m_1=-\frac{1}{m_2}[/latex]
    • Vertical lines and horizontal lines are always perpendicular to each other.

Self Check

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Glossary

geoboard
A geoboard is a board with a grid of pegs on it.
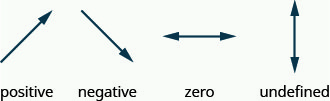
negative slope
A negative slope of a line goes down as you read from left to right.
positive slope
A positive slope of a line goes up as you read from left to right.
rise
The rise of a line is its vertical change.
run
The run of a line is its horizontal change.
slope formula
The slope of the line between two points [latex](x_1,y_1)[/latex] and [latex](x_2,y_2)[/latex] is [latex]m=\frac{y_2-y_1}{x_2-x_1}[/latex]
slope of a line
The slope of a line is [latex]m=\frac{rise}{run}[/latex]. The rise measures the vertical change and the run measures the horizontal change.
parallel lines
Lines in the same plane that do not intersect.
perpendicular lines
Lines in the same plane that form a right angle.
slope-intercept form of an equation of a line
The slope–intercept form of an equation of a line with slope [latex]m[/latex] and [latex]y[/latex]-intercept, [latex](0,b)[/latex] is, [latex]y=mx+b[/latex].
definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Fanshawe Pre-Health Sciences Mathematics 1 Copyright © 2022 by Domenic Spilotro, MSc is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book