4.3 Solve Systems of Equations by Elimination

Learning Objectives

By the end of this section, you will be able to:

  • Solve a system of equations by elimination
  • Solve applications of systems of equations by elimination
  • Choose the most convenient method to solve a system of linear equations

Try It

Before you get started, take this readiness quiz.

1) Simplify [latex]-5\left(6-3a\right)[/latex].
2) Solve the equation [latex]\frac{1}{3}x+\frac{5}{8}=\frac{31}{24}[/latex].

We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.

The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.

Solve a System of Equations by Elimination

The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.

For any expressions [latex]a[/latex], [latex]b[/latex], [latex]c[/latex], and [latex]d[/latex],

[latex]\begin{array}{cccc}\text{if}& a& =& b\\ \text{and}& c& =& d\\ \text{then}& a+c& =& b+d\end{array}[/latex]

To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.

Notice how that works when we add these two equations together:

[latex]\begin{array}{r}3x+y&=&5\\2x-y&=&0\\\hline5x&=&5\end{array}[/latex]

The [latex]y[/latex]’s add to zero and we have one equation with one variable.

Let’s try another one:

[latex]\begin{array}{c}x+4y&=&2\\2x+5y&=&-2\end{array}[/latex]

This time we don’t see a variable that can be immediately eliminated if we add the equations.

But if we multiply the first equation by [latex]−2[/latex], we will make the coefficients of [latex]x[/latex] opposites. We must multiply every term on both sides of the equation by [latex]−2[/latex].

[latex]\begin{eqnarray*}-2(x+4y)&=&-2(2)\\2x+5y&=&-2\\-2x-8y&=&-4\\2x+5y&=&-2\end{eqnarray*}[/latex]

Now we see that the coefficients of the [latex]x[/latex] terms are opposites, so [latex]x[/latex] will be eliminated when we add these two equations.

Add the equations yourself—the result should be [latex]−3y =−6[/latex]. And that looks easy to solve, doesn’t it? Here is what it would look like.

[latex]\begin{array}{c} \Bigg\{ \begin{array}{c} \phantom{}-2x-8y=-4 \\ \underline{\text{}}{\rule{1em}{0ex}}{2x+5y=-2} \\ \rule{3cm}{0.2mm} \end{array}\\ -3y=-6 \end{array}[/latex]

We’ll do one more:

[latex]\begin{array}{c}4x-3y&=&10\\3x+5y&=&-7\end{array}[/latex]

It doesn’t appear that we can get the coefficients of one variable to be opposites by multiplying one of the equations by a constant, unless we use fractions. So instead, we’ll have to multiply both equations by a constant.

We can make the coefficients of [latex]x[/latex] be opposites if we multiply the first equation by [latex]3[/latex] and the second by [latex]−4[/latex], so we get [latex]12x[/latex] and [latex]−12x[/latex].

[latex]\begin{eqnarray*}(4x-3y)&=&3(10)\\-4(3x+5y)&=&-4(-7)\end{eqnarray*}[/latex]

This gives us these two new equations:

[latex]\begin{eqnarray*}12x-9y&=&30\\-12x+20y&=&28\end{eqnarray*}[/latex]

When we add these equations,

[latex]\begin{array}{r}12x-9y=30\\-12x+20y=28\\\hline-29y=58\end{array}[/latex]

the [latex]x[/latex]’s are eliminated and we just have [latex]−29y=58[/latex].

Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.

Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.

Example 4.3.1

How to Solve a System of Equations by Elimination

Solve the system by elimination.

[latex]\begin{array}{c}2x+y=7\\x-2y=6\end{array}[/latex]

Solution
This figure has seven rows and three columns. The first row reads, “Step 1: Write both equations in standard form. If any coefficients are fractions, clear them.” It also says, “Both equations are in standard form, A x + B y = C. There are no fractions.” It also gives the two equations as 2x + y = 7 and x – 2y = 6.
Figure 4.3.1
The second row reads, “Step 2: Make the coefficients of one variable opposites. Decide which variable you will eliminate. Multiply one or both equations so that the coefficients of that variable are opposites.” It also says, “We can eliminate the y’s by multiplying the first equation by 2. Multiply both sides of 2x + y = 7 by 2.” It also shows the steps with equations. Initially the equations are ex + y = 7 and x – 2y = 6. Then they become 2(2x + y) = 2 times 7 and x – 2y = 6. They then become 4x + 2y = 14 and x – 2y = 6.
Figure 4.3.2
The third row says, “Step 3: Add the equations resulting from step 2 to eliminate one variable.” It also says, “We add the x’s, y’s, and constants.” It then gives the equation as 5x = 20.
Figure 4.3.3
The fourth row says, “Step 4: Solve for the remaining variable.” It also says, “Solve for x.” It gives the equation as x = 4.
Figure 4.3.4
The fifth row says, “Step 5: Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.” It also says, “Substitute x = 4 into the second equation, x – 2y = 6. Then solve for y.” It then gives the equations as x – 2y = 6 which becomes 4 – 2y = 6. This is then −2y = 2, and thus, y = −1.
Figure 4.3.5
The sixth row says, “Step 6: Write the solution as an order pair.” It also says, “Write it as (x, y).” It gives the ordered pair as (4, −1).
Figure 4.3.6
The seventh row says, “Step 7: Check that the ordered pair is a solution to both original equations.” It also says, “Substitute (4, −1) into 2x + y = 7 and x – 2y = 6. Do they make both equations true? Yes!” It then gives the equations. 2x + y = 7 becomes 2 times 4 + −1 = 7 which is 7 = 7. x – 2y = 6 becomes 4 – 2 times −1 = 6 which is 6 = 6. The row then says, “The solution is (4, −1).”
Figure 4.3.7

Try It

3) Solve the system by elimination.

[latex]\begin{eqnarray*}3x+y&=&5\\2x-3y&=&7\end{eqnarray*}[/latex]

Solution

[latex]\left(2,-1\right)[/latex]

4) Solve the system by elimination.

[latex]\begin{eqnarray*}4x+y&=&-5\\-2x-2y&=&-2\end{eqnarray*}[/latex]

Solution

[latex]\left(-2,3\right)[/latex]

HOW TO

How to solve a system of equations by elimination.

  1. Write both equations in standard form. If any coefficients are fractions, clear them.
  2. Make the coefficients of one variable opposites.
    • Decide which variable you will eliminate.
    • Multiply one or both equations so that the coefficients of that variable are opposites.
  3. Add the equations resulting from Step 2 to eliminate one variable.
  4. Solve for the remaining variable.
  5. Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
  6. Write the solution as an ordered pair.
  7. Check that the ordered pair is a solution to both original equations.

First we’ll do an example where we can eliminate one variable right away.

Example 4.3.2

Solve the system by elimination.

[latex]\begin{array}{c}x+y=10\\ x-y=12\end{array}[/latex]

Solution

[latex]\left\{\begin{array}{l}x+y=10\\x-y=12\end{array}\right.[/latex]

Both equations are in standard form.

The coefficients of [latex]y[/latex] are already opposites.

Step 1: Add the two equations to eliminate [latex]y[/latex].

The resulting equation has only 1 variable, [latex]x[/latex].

[latex]\begin{array}{r}\left\{\begin{array}{l}x+y&=&10\\x-y&=&12\end{array}\right.\\\hline&2x=22&\end{array}[/latex]

Step 2: Solve for [latex]x[/latex], the remaining variable.

Step 3: Substitute [latex]x = 11[/latex] into one of the original equations.

x=11 x+y=10
Figure 4.3.8

[latex]{\color{red}{11}}{+y=10}[/latex]

Step 4: Solve for the other variable, [latex]y[/latex].

[latex]y=-1[/latex]

Step 5: Write the solution as an ordered pair.

The ordered pair is [latex](11,−1)[/latex].

Step 6. Check that the ordered pair is a solution to both original equations.

[latex]\begin{eqnarray*}\text{Equation 1:}\;x\;+\;y\;&=&\;10\\11+(-1)&\overset?=&10\\10&=&10\;\checkmark\\\\\text{Equation 2:}\;x-y&=&12\\11-(-1)&\overset?=&12\\12&=&12\;\checkmark\end{eqnarray*}[/latex]

The solution is [latex](11,−1)[/latex].

Try It

5) Solve the system by elimination.

[latex]\begin{eqnarray*}2x+y&=&5\\x-y&=&4\end{eqnarray*}[/latex]

Solution

[latex]\left(3,-1\right)[/latex]

6) Solve the system by elimination.

[latex]\begin{eqnarray*}x+y&=&3\\-2x-y&=&-1\end{eqnarray*}[/latex]

Solution

[latex]\left(-2,5\right)[/latex]

In Example 4.3.3, we will be able to make the coefficients of one variable opposites by multiplying one equation by a constant.

Example 4.3.3

Solve the system by elimination.

[latex]\begin{array}{c}3x-2y=-2\\ 5x-6y=10\end{array}[/latex]

Solution

[latex]\left\{\begin{array}{l}3x-2y=-2\\5x-6y=10\end{array}\right.[/latex]

Both equations are in standard form.

None of the coefficients are opposites.

Step 1: We can make the coefficients of [latex]y[/latex] opposites by multiplying the first equation by [latex]−3[/latex].

[latex]\left\{\begin{array}{l}{\color{red}{-}}{\color{red}{3}}(3x-2y)={\color{red}{-}}{\color{red}{3}}(-2)\\5x-6y=10\end{array}\right.[/latex]

Step 2: Simplify.

[latex]\left\{\begin{array}{l}-9x+6y=6\\5x-6y=10\end{array}\right.[/latex]

Step 3: Add the two equations to eliminate [latex]y[/latex].

[latex]\begin{array}{r}\left\{\begin{array}{l}-9x+6y=6\\5x-6y=10\end{array}\right.\\\hline&-4x=16&\end{array}[/latex]

Step 4: Solve for the remaining variable, [latex]x[/latex].

Step 5: Substitute [latex]x=−4[/latex] into one of the original equations.

x=-4 3x-2y=-2
Figure 4.3.9

[latex]{3(}{\color{red}{-}}{}{\color{red}{4}}{)-2y=-2}[/latex]

Step 6: Solve for [latex]y[/latex].

[latex]\begin{eqnarray*}-12-2y&=&-2\\-2y&=&10\\y&=&-5\end{eqnarray*}[/latex]

Step 7: Write the solution as an ordered pair.

The ordered pair is [latex](−4, −5)[/latex].

Step 8: Check that the ordered pair is a solution to both original equations.

[latex]\begin{eqnarray*}\text{Equation 1:}\;3x-2y&=&-2\\3(-4)-2(-5)&\overset?=&-2\\-12+10&\overset?=&-2\\-2&=&-2\;\checkmark\\\\\text{Equation 2:}\;5x-6y&=&10\\3(-4)-6(-5)&\overset?=&10\\-20+30&\overset?=&10\\10&=&10\checkmark\end{eqnarray*}[/latex]

The solution is [latex](−4, −5)[/latex].

Try It

7) Solve the system by elimination.

[latex]\begin{eqnarray*}4x-3y&=&1\\5x-9y&=&-4\end{eqnarray*}[/latex]

Solution

[latex]\left(1,1\right)[/latex]

8) Solve the system by elimination.

[latex]\begin{eqnarray*}3x+2y&=&2\\6x+5y&=&8\end{eqnarray*}[/latex]

Solution

[latex]\left(-2,4\right)[/latex]

Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.

Example 4.3.4

Solve the system by elimination. [latex]\begin{array}{c}4x-3y=9\\ 7x+2y=-6\end{array}[/latex]

Solution

In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by a constant to get the opposites.

[latex]\left\{\begin{array}{l}4x-3y=9\\7x+2y=-6\end{array}\right.[/latex]

Step 1: Both equations are in standard form. To get opposite coefficients of [latex]y[/latex], we will multiply the first equation by [latex]2[/latex] and the second equation by [latex]3[/latex].

[latex]\left\{\begin{array}{l}{\color{red}{-}}{\color{red}{3}}(3x-2y)={\color{red}{-}}{\color{red}{3}}(-2)\\5x-6y=10\end{array}\right.[/latex]

Step 2: Simplify.

[latex]\left\{\begin{array}{l}8x-6y=18\\21x+6y=-18\end{array}\right.[/latex]

Step 3: Add the two equations to eliminate [latex]y[/latex].

[latex]\begin{array}{r}\left\{\begin{array}{l}8x-6y=18\\21x+6y=-18\end{array}\right.\\\hline39x=0\end{array}[/latex]

Step 4: Solve for [latex]x[/latex].

Step 5: Substitute [latex]x = 0[/latex] into one of the original equations.

x=0 7x+2y=-6
Figure 4.3.10

[latex]{7\times}{\color{red}{0}}{+2y=-6}[/latex]

Step 6: Solve for [latex]y[/latex].

[latex]2y=-6[/latex]

[latex]y=-3[/latex]

Step 7: Write the solution as an ordered pair.

The ordered pair is [latex](0, −3)[/latex].

Step 8: Check that the ordered pair is a solution to both original equations.

[latex]\begin{array}{cccc}\begin{array}{ccc}4x-3y& =& 9\\ 4\left(0\right)-3\left(-3\right)& \stackrel{?}{=}& 9\\ 9& =& 9✓\end{array}& & & \begin{array}{ccc}7x+2y& =& -6\\ 7\left(0\right)+2\left(-3\right)& \stackrel{?}{=}& -6\\ -6& =& -6✓\end{array}\end{array}[/latex]

The solution is [latex](0, −3)[/latex].

What other constants could we have chosen to eliminate one of the variables? Would the solution be the same?

Try It

9) Solve the system by elimination.

[latex]\begin{eqnarray*}3x-4y&=&-9\\ 5x+3y&=&14\end{eqnarray*}[/latex]

Solution

[latex]\left(1,3\right)[/latex]

10) Solve the system by elimination.

[latex]\begin{eqnarray*}7x+8y&=&4\\ 3x-5y&=&27\end{eqnarray*}[/latex]

Solution

[latex]\left(4,-3\right)[/latex]

When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by its LCD.

Example 4.3.5

Solve the system by elimination.

[latex]\begin{array}{c}x+\frac{1}{2}y=6\\ \frac{3}{2}x+\frac{2}{3}y=\frac{17}{2}\end{array}[/latex]

Solution

In this example, both equations have fractions. Our first step will be to multiply each equation by its LCD to clear the fractions.

[latex]\left\{\begin{array}{l}x+\frac12y=6\\\frac32x+\frac23y=\frac{17}2\end{array}\right.[/latex]

Step 1: To clear the fractions, multiply each equation by its LCD.

[latex]\left\{\begin{array}{l}{\color{red}{2}}(x+\frac12y)={\color{red}{2}}(6)\\{\color{red}{6}}(\frac32x+\frac23y)={\color{red}{6}}(\frac{17}2)\end{array}\right.[/latex]

Step 2: Simplify.

[latex]\left\{\begin{array}{l}2x+y=12\\9x+4y=51\end{array}\right.[/latex]

Now we are ready to eliminate one of the variables. Notice that both equations are in standard form.

Step 3: We can eliminate [latex]y[/latex] multiplying the top equation by [latex]−4[/latex].

[latex]\left\{\begin{array}{l}{\color{red}{-}}{\color{red}{4}}(2x+y)={\color{red}{-}}{\color{red}{4}}(12)\\9x+4y=51\end{array}\right.[/latex]

Step 4: Simplify and add.

Step 5: Substitute [latex]x = 3[/latex] into one of the original equations.

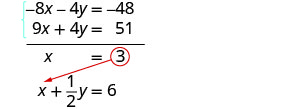
-8x-4y=-48 9x+4y=51 ---------- x=3 x+1/2y=6
Figure 4.3.11

Step 6: Solve for [latex]y[/latex].

[latex]\begin{eqnarray*}{\color{red}{3}}+\frac12y&=&6\\\frac12y&=&3\\y&=&6\end{eqnarray*}[/latex]

Step 7: Write the solution as an ordered pair.

The ordered pair is [latex](3, 6)[/latex].

Step 8: Check that the ordered pair is a solution to both original equations.

[latex]\begin{eqnarray*}\text{Equation 1:}\;x+\frac12y=6\\3+\frac12(6)\overset?=6\\3+3=6\\6=6\\\text{Equation 2:}\;\frac32x+\frac23y=\frac{17}2\\ \frac32(3)+\frac23(6)\overset?=\frac{17}2\\ \frac92+4\overset?=\frac{17}2\\ \frac92+\frac82\overset?=\frac{17}2\\ \frac{17}2=\frac{17}2\\\end{eqnarray*}[/latex]

The solution is [latex](3, 6)[/latex].

Try It

11) Solve the system by elimination.

[latex]\begin{eqnarray*}\frac{1}{3}x-\frac{1}{2}y&=&1\\ \frac{3}{4}x-y&=&\frac{5}{2}\end{eqnarray*}[/latex]

Solution

[latex]\left(6,2\right)[/latex]

12) Solve the system by elimination.

[latex]\begin{eqnarray*}x+\frac{3}{5}y&=&-\frac{1}{5}\\ -\frac{1}{2}x-\frac{2}{3}y&=&\frac{5}{6}\end{eqnarray*}[/latex]

Solution

[latex]\left(1,-2\right)[/latex]

In the Solving Systems of Equations by Graphing we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.

Example 4.3.6

Solve the system by elimination. [latex]\begin{eqnarray*}3x+4y&=&12\\ y&=&3-\frac{3}{4}x\end{eqnarray*}[/latex]

Solution

[latex]\begin{eqnarray*}\left\{\begin{array}{l}23x+4y=12\\y=3-\frac34x\end{array}\right.\end{eqnarray*}[/latex]

Step 1: Write the second equation in standard form.

[latex]\begin{eqnarray*}\left\{\begin{array}{l}23x+4y=12\\y=3-\frac34x\end{array}\right.\end{eqnarray*}[/latex]

Step 2: Clear the fractions by multiplying the second equation by [latex]4[/latex].

[latex]\begin{eqnarray*}\left\{\begin{array}{l}3x+4y=12\\{\color{red}{4}}\left(\frac34x+y\right)={\color{red}{4}}(3)\end{array}\right.\end{eqnarray*}[/latex]

Step 3: Simplify.

[latex]\begin{eqnarray*}\left\{\begin{array}{l}3x+4y=12\\3x+4y=12\end{array}\right.\\\end{eqnarray*}[/latex]

Step 4: To eliminate a variable, we multiply the second equation by [latex]-1[/latex].

Step 5: Simplify and add.

[latex]\begin{eqnarray*}\left\{\begin{array}{l}3x+4y=12\\\underline{-3x-4y=12}\end{array}\right.\\0=0\\\end{eqnarray*}[/latex]

This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions.

After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.

Try It

13) Solve the system by elimination.

[latex]\begin{eqnarray*}5x-3y&=&15\\ y&=&-5+\frac{5}{3}x\end{eqnarray*}[/latex]

Solution

Infinitely many solutions.

14) Solve the system by elimination.

[latex]\begin{eqnarray*}x+2y&=&6\\ y&=&-\frac{1}{2}x+3\end{eqnarray*}[/latex]

Solution

Infinitely many solutions.

Example 4.3.7

Solve the system by elimination. [latex]\begin{eqnarray*}-6x+15y&=&10\\ 2x-5y&=&-5\end{eqnarray*}[/latex]

Solution

Step 1: The equations are in standard form.

[latex]\left\{\begin{array}{l}-6x+15y=10\\2x-5y=-5\end{array}\right.[/latex]

Step 2: Multiply the second equation by [latex]3[/latex] to eliminate a variable.

[latex]\left\{\begin{array}{l}-6x+15y=10\\{\color{red}{3}}(2x-5y)={\color{red}{3}}(-5)\end{array}\right.[/latex]

Step 3: Simplify and add.

[latex]\begin{eqnarray*}\left\{\begin{array}{l}-6x+15y=10\\\underline{-6x-15y=-15}\end{array}\right.\\0\neq-5\end{eqnarray*}[/latex]

This statement is false. The equations are inconsistent and so their graphs would be parallel lines.

The system does not have a solution.

Try It

15) Solve the system by elimination.

[latex]\begin{eqnarray*}-3x+2y&=&8\\9x-6y&=&13\end{eqnarray*}[/latex]

Solution

No solution.

16) Solve the system by elimination.

[latex]\begin{eqnarray*}7x-3y&=&-2\\-14x+6y&=&8\end{eqnarray*}[/latex]

Solution

No solution.

Solve Applications of Systems of Equations by Elimination

Some applications problems translate directly into equations in standard form, so we will use the elimination method to solve them. As before, we use our Problem Solving Strategy to help us stay focused and organized.

Example 4.3.8

The sum of two numbers is [latex]39[/latex]. Their difference is [latex]9[/latex]. Find the numbers.

Solution

Step 1: Read the problem.

Step 2: Identify what we are looking for.

We are looking for two numbers.

Step 3: Name what we are looking for.

Choose a variable to represent that quantity.

Let [latex]n=[/latex] the first number.

Let [latex]m=[/latex] the second number.

Step 4: Translate into a system of equations.

The system is:

The sum of two numbers is [latex]39[/latex].

[latex]n+m=39[/latex]

Their difference is [latex]9[/latex].

[latex]\begin{align*}n-m&=9\\n+m&=39\\n-m&=9\end{align*}[/latex]

Step 5: Solve the system of equations.

To solve the system of equations, use elimination.

The equations are in standard form and the coefficients of [latex]m[/latex] are opposites. Add.

Solve for [latex]n[/latex].

Substitute [latex]n=24[/latex] into one of the original equations and solve for [latex]m[/latex].

[latex]\begin{array}{r}\left\{\begin{array}{l}n+m&=39\\-n-m=9\end{array}\right.\\\hline2n&=48\end{array}[/latex]

[latex]\begin{eqnarray*}n&=&24\\n+m&=&39\\24+m&=&39\\m&=&15\end{eqnarray*}[/latex]

Step 6: Check the answer.

Since [latex]24+15=39[/latex] and [latex]24-15=9[/latex], the answers check.

Step 7: Answer the question.

The numbers are [latex]24[/latex] and [latex]15[/latex].

Try It

17) The sum of two numbers is [latex]42[/latex]. Their difference is [latex]8[/latex]. Find the numbers.

Solution

The numbers are [latex]25[/latex] and [latex]17[/latex].

18) The sum of two numbers is [latex]−15[/latex]. Their difference is [latex]−35[/latex]. Find the numbers.

Solution

The numbers are [latex]−25[/latex] and [latex]10[/latex].

Example 4.3.9

Joe stops at a burger restaurant every day on his way to work. Monday he had one order of medium fries and two small sodas, which had a total of [latex]620[/latex] calories. Tuesday he had two orders of medium fries and one small soda, for a total of [latex]820[/latex] calories. How many calories are there in one order of medium fries? How many calories in one small soda?

Solution

Step 1: Read the problem.

Step 2: Identify what we are looking for.

We are looking for the number of calories in one order of medium fries and in one small soda.

Step 3: Name what we are looking for.

Let [latex]f =[/latex] the number of calories in [latex]1[/latex] order of medium fries.

Let [latex]s =[/latex] the number of calories in [latex]1[/latex] small soda.

Step 4: Translate into a system of equations:

Our system is:

one medium fries and two small sodas had a total of [latex]620[/latex] calories

[latex]f+2s=620[/latex]

two medium fries and one small soda had a total of [latex]820[/latex] calories.

[latex]2f+s=820[/latex]

[latex]\left\{\begin{array}{l}f+2s=620\\2f+s=820\end{array}\right.[/latex]

Step 5: Solve the system of equations.

To solve the system of equations, use elimination. The equations are in standard form. To get opposite coefficients of [latex]f[/latex], multiply the top equation by [latex]−2[/latex].Simplify and add.Solve for [latex]s[/latex].Substitute [latex]s = 140[/latex] into one of the original equations and then solve for [latex]f[/latex].

[latex]\left\{\begin{array}{l}{\color{red}{-}}{\color{red}{2}}(f+2s)={\color{red}{-}}{\color{red}{2}}(620)\\2f+s=820\end{array}\right.[/latex]

[latex]\begin{array}{r}\left\{\begin{array}{l}-2f-4s=-1240\\2f+s=820\end{array}\right.\\\hline-3s=-420\end{array}[/latex]

[latex]\begin{eqnarray*}{\color{red}{s}}&=&{\color{red}{140}}\\f+2s&=&620\\f+2\times{\color{red}{140}}&=&620\\f+280&=&620\\f&=&340\end{eqnarray*}[/latex]

Step 6: Check the answer.

Verify that these numbers make sense in the problem and that they are solutions to both equations. We leave this to you!

Step 7: Answer the question.

The small soda has [latex]140[/latex] calories and the fries have [latex]340[/latex] calories.

Try It

19) Malik stops at the grocery store to buy a bag of diapers and [latex]2[/latex] cans of formula. He spends a total of [latex]$37[/latex]. The next week he stops and buys [latex]2[/latex] bags of diapers and [latex]5[/latex] cans of formula for a total of [latex]$87[/latex]. How much does a bag of diapers cost? How much is one can of formula?

Solution

The bag of diapers costs [latex]$11[/latex] and the can of formula costs [latex]$13[/latex].

20) To get her daily intake of fruit for the day, Sasha eats a banana and [latex]8[/latex] strawberries on Wednesday for a calorie count of [latex]145[/latex]. On the following Wednesday, she eats two bananas and [latex]5[/latex] strawberries for a total of [latex]235[/latex] calories for the fruit. How many calories are there in a banana? How many calories are in a strawberry?

Solution

There are [latex]105[/latex] calories in a banana and [latex]5[/latex] calories in a strawberry.

Choose the Most Convenient Method to Solve a System of Linear Equations

When you will have to solve a system of linear equations in a later math class, you will usually not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.

This table has two rows and three columns. The first row labels the columns as “Graphing,” “Substitution,” and “Elimination.” Under “Graphing” it says, “Use when you need a picture of the situation.” Under “Substitution” it says, “Use when one equation is already solved for one variable.” Under “Elimination” it says, “Use when the equations are in standard form.”
Figure 4.1.1

Example 4.3.10

For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

a.

[latex]\begin{eqnarray*}3x+8y&=&40\\ 7x-4y&=&-32\end{eqnarray*}[/latex]

b.

[latex]\begin{eqnarray*}5x+6y&=&12\\ y&=&\frac{2}{3}x-1\end{eqnarray*}[/latex]

Solution

a.

[latex]\begin{align*}3x+8y&=40\\7x-4y&=-32\end{align*}[/latex]

Since both equations are in standard form, using elimination will be most convenient.

b.

[latex]\begin{align*}5x+6y&=12\\y&=\frac{2}{3}x-1\end{align*}[/latex]

Since one equation is already solved for [latex]y[/latex], using substitution will be most convenient.

Try It

21) For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

a.

[latex]\begin{eqnarray*}4x-5y&=&-32\\ 3x+2y&=&-1\end{eqnarray*}[/latex]

b.

[latex]\begin{eqnarray*}x&=&2y-1\\ 3x-5y&=&-7\end{eqnarray*}[/latex]

Solution

a. Since both equations are in standard form, using elimination will be most convenient.
b. Since one equation is already solved for [latex]x[/latex], using substitution will be most convenient.

22) For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

a.

[latex]\begin{eqnarray*}y&=&2x-1\\ 3x-4y&=&-6\end{eqnarray*}[/latex]

b.

[latex]\begin{eqnarray*}6x-2y&=&12\\3x+7y&=&-13\end{eqnarray*}[/latex]

Solution

a. Since one equation is already solved for [latex]y[/latex], using substitution will be most convenient
b. Since both equations are in standard form, using elimination will be most convenient.

Access these online resources for additional instruction and practice with solving systems of linear equations by elimination.

Key Concepts

  • To Solve a System of Equations by Elimination
    1. Write both equations in standard form. If any coefficients are fractions, clear them.
    2. Make the coefficients of one variable opposites.
      • Decide which variable you will eliminate.
      • Multiply one or both equations so that the coefficients of that variable are opposites.
    3. Add the equations resulting from Step 2 to eliminate one variable.
    4. Solve for the remaining variable.
    5. Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.
    6. Write the solution as an ordered pair.
    7. Check that the ordered pair is a solution to both original equations.

Self Check

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

What does this checklist tell you about your mastery of this section? What steps will you take to improve?

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Fanshawe Pre-Health Sciences Mathematics 1 Copyright © 2022 by Domenic Spilotro, MSc is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book