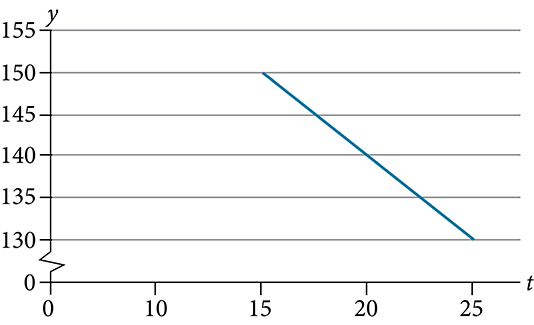Exercises: Linear Functions and Applications of Linear Functions (3.12)

Exercises: Verbal Problems

Instructions: For questions 1-7, answer the given verbal word problems.
1. Terry is skiing down a steep hill. Terry’s elevation, [latex]E(t)[/latex], in feet after [latex]t[/latex] seconds is given by [latex]E(t)=3000-70t[/latex]. Write a complete sentence describing Terry’s starting elevation and how it is changing over time.
Solution

Terry starts at an elevation of [latex]3000[/latex] feet and descends [latex]70[/latex] feet per second.

2. Jessica is walking home from a friend’s house. After [latex]2[/latex] minutes she is [latex]1.4[/latex] miles from home. Twelve minutes after leaving, she is [latex]0.9[/latex] miles from home. What is her rate in miles per hour?
3. A boat is [latex]100[/latex] miles away from the marina, sailing directly toward it at [latex]10[/latex] miles per hour. Write an equation for the distance of the boat from the marina after [latex]t[/latex] hours.
Solution

[latex]d(t)=100-10t[/latex]

4. Explain how to find the output variable in a word problem that uses a linear function.
5. Explain how to find the input variable in a word problem that uses a linear function.
Solution

Determine the independent variable. This is the variable upon which the output depends.

6. Explain how to determine the slope in a word problem that uses a linear function.
7. Explain how to interpret the initial value in a word problem that uses a linear function.
Solution

To determine the initial value, find the output when the input is equal to zero.

Exercises: Algebraic Problems

Instructions: For questions 8-9, consider this scenario: A town’s population has been decreasing at a constant rate. In 2010 the population was [latex]5\text{,}900[/latex]. By 2012 the population had dropped [latex]4\text{,}700[/latex]. Assume this trend continues.

8. Predict the population in 2016.

Solution

[latex]2\text{,}300[/latex]

9. Identify the year in which the population will reach [latex]0[/latex].

Exercises: Algebraic Problems

Instructions: For questions 10-11, consider this scenario: A town’s population has been increasing at a constant rate. In 2010 the population was [latex]46\text{,}020[/latex]. By 2012 the population had increased to [latex]52\text{,}070[/latex]. Assume this trend continues.

10. Predict the population in 2016.
Solution

[latex]64\text{,}170[/latex]

11. Identify the year in which the population will reach [latex]75\text{,}000[/latex].

Exercises: Algebraic Problems

Instructions: For questions 12-17, consider this scenario: A town has an initial population of [latex]75\text{,}000[/latex]. It grows at a constant rate of [latex]2\text{,}500[/latex] per year for [latex]5[/latex] years.

12. Find the linear function that models the town’s population [latex]P[/latex]as a function of the year, [latex]t[/latex], where[latex]t[/latex]is the number of years since the model began.

Solution

[latex]P(t)=75,000+2500t[/latex]

13. Find a reasonable domain and range for the function [latex]P[/latex].
14. If the function [latex]P[/latex] is graphed, find and interpret the [latex]x[/latex]– and [latex]y[/latex]-intercepts.
Solution

[latex](–30,0)[/latex] Thirty years before the start of this model, the town had no citizens.
[latex](0,75\text{,}000)[/latex] Initially, the town had a population of [latex]75\text{,}000[/latex].

15. If the function [latex]P[/latex] is graphed, find and interpret the slope of the function.
16. When will the population reach [latex]100\text{,}000[/latex]?
Solution

Ten years after the model began

17. What is the population in the year [latex]12[/latex] years from the onset of the model?

Exercises: Algebraic Problems

Instructions: For questions 18-23, consider this scenario: The weight of a newborn is [latex]7.5[/latex] pounds. The baby gained one-half pound a month for its first year.

18. Find the linear function that models the baby’s weight [latex]W[/latex]as a function of the age of the baby, in months, [latex]t[/latex].
Solution

[latex]W(t)=0.5t+7.5[/latex]

19. Find a reasonable domain and range for the function [latex]W[/latex].
20. If the function [latex]W[/latex] is graphed, find and interpret the [latex]x[/latex]– and [latex]y[/latex]-intercepts.
Solution

[latex](-15,0)[/latex]: The [latex]x[/latex]-intercept is not a plausible set of data for this model because it means the baby weighed [latex]0[/latex] pounds 15 months prior to birth. [latex](0,7.5)[/latex]: The baby weighed [latex]7.5[/latex] pounds at birth.

21. If the function [latex]W[/latex] is graphed, find and interpret the slope of the function.
22. When did the baby weight [latex]10.4[/latex] pounds?
Solution

At age [latex]5.8[/latex] months

23. What is the output when the input is [latex]6.2[/latex]?

Exercises: Algebraic Problems

Instructions: For questions 24-29, consider this scenario: The number of people afflicted with the common cold in the winter months steadily decreased by [latex]205[/latex] each year from 2005 until 2010. In 2005, [latex]12\text{,}025[/latex] people were inflicted.

24. Find the linear function that models the number of people inflicted with the common cold [latex]C[/latex] as a function of the year, [latex]t[/latex].

Solution

[latex]C(t)=12\text{,}025-205t[/latex]

25. Find a reasonable domain and range for the function [latex]C[/latex].
26. If the function [latex]C[/latex] is graphed, find and interpret the [latex]x[/latex]– and [latex]y[/latex]-intercepts.
Solution

[latex](58.7,0)[/latex]: In roughly [latex]59[/latex] years, the number of people inflicted with the common cold would be [latex]0[/latex].
[latex](0,12\text{,}025)[/latex]: Initially there were [latex]12\text{,}025[/latex] people afflicted by the common cold.

27. If the function [latex]C[/latex] is graphed, find and interpret the slope of the function.
28. When will the output reach [latex]0[/latex]?
Solution

2063

29. In what year will the number of people be [latex]9\text{,}700[/latex]?

Exercises: Graphical Problems

Instructions: For questions 30-33, use the graph in Figure 3P.12.1, which shows the profit, [latex]y[/latex], in thousands of dollars, of a company in a given year, [latex]t[/latex], where [latex]t[/latex] represents the number of years since 1980.

Graph of a decreasing line from (15, 150) to (25, 130). The x-axis goes from 0 to 30 in intervals of 5 and the y-axis goes from 125 to 155 in intervals of 5.
Figure 3P.12.1
30. Find the linear function[latex]y[/latex], where[latex]y[/latex] depends on [latex]t[/latex], the number of years since 1980.
Solution

[latex]y=-2t+180[/latex]

31. Find and interpret the [latex]y[/latex]-intercept.
32. Find and interpret the [latex]x[/latex]-intercept.
Solution

In 2070, the company’s profit will be zero.

33. Find and interpret the slope.

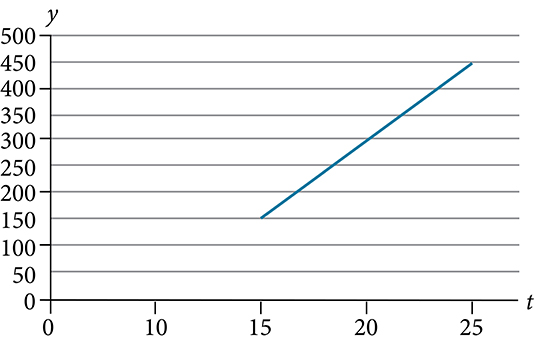
Exercises: Graphical Problems

Instructions: For questions 34-37, use the graph in Figure 3P.12.2, which shows the profit, [latex]y[/latex],in thousands of dollars, of a company in a given year, [latex]t[/latex],where[latex]t[/latex]represents the number of years since 1980.

Graph of a line from (15, 150) to (25, 450). The x-axis goes from 0 to 30 in intervals of 5 and the y-axis goes from 0 to 500 in intervals of 50.
Figure 3P.12.2
34. Find the linear function[latex]y[/latex], where [latex]y[/latex] depends on [latex]t[/latex], the number of years since 1980.
Solution

[latex]y=30t-300[/latex]

35. Find and interpret the [latex]y[/latex]-intercept.
Solution

[latex](0,-300)[/latex] In 1980, the company lost [latex]$300\text{,}000[/latex].

36. Find and interpret the [latex]x[/latex]-intercept.
37. Find and interpret the slope.
Solution

[latex]y=30t-300[/latex] of form [latex]y=mx+b,m=30[/latex]. For each year after 1980, the company’s profits increased [latex]$30\text{,}000[/latex] per year

Exercises: Numeric Problems

Instructions: For questions 38-40, use the median home values in Mississippi and Hawaii (adjusted for inflation) shown in Table 3P.12.1. Assume that the house values are changing linearly.

Table 3P.12.1: Median Home Values of Mississipi and Hawaii in 1950 and 2000
Year Mississippi Hawaii
1950 [latex]$25\text{,}200[/latex] [latex]$74\text{,}400[/latex]
2000 [latex]$71\text{,}400[/latex] [latex]$272\text{,}700[/latex]
38. In which state have home values increased at a higher rate?
39. If these trends were to continue, what would be the median home value in Mississippi in 2010?
Solution

[latex]$80\text{,}640[/latex]

40. If we assume the linear trend existed before 1950 and continues after 2000, the two states’ median house values will be (or were) equal in what year? (The answer might be absurd.)

Exercises: Numeric

Instructions: For questions 41-43, use the median home values in Indiana and Alabama (adjusted for inflation) shown in (Figure). Assume that the house values are changing linearly.

Table 3P.12.2: Median Home Values of Indiana and Alabama in 1950 and 2000
Year Indiana Alabama
1950 $37,700 $27,100
2000 $94,300 $85,100
41. In which state have home values increased at a higher rate?
Solution

Alabama

42. If these trends were to continue, what would be the median home value in Indiana in 2010?
43. If we assume the linear trend existed before 1950 and continues after 2000, the two states’ median house values will be (or were) equal in what year? (The answer might be absurd.)
Solution

2328

Exercises: Real-World Applications

Instructions: For questions 44-66, solve the given real-world application problems.
44. At noon, a barista notices that she has [latex]$20[/latex] in her tip jar. If she makes an average of [latex]$0.50[/latex] from each customer, how much will she have in her tip jar if she serves[latex]n[/latex]more customers during her shift?
Solution

[latex]20+0.5n[/latex]

45. A gym membership with two personal training sessions costs [latex]$125[/latex], while gym membership with five personal training sessions costs [latex]$260[/latex]. What is cost per session?
46. A clothing business finds there is a linear relationship between the number of shirts, [latex]n[/latex], it can sell and the price, [latex]p[/latex], it can charge per shirt. In particular, historical data shows that [latex]1\text{,}000[/latex] shirts can be sold at a price of [latex]$30[/latex], while [latex]3\text{,}000[/latex] shirts can be sold at a price of [latex]$22[/latex]. Find a linear equation in the form [latex]p(n)=mn+b[/latex] that gives the price [latex]p[/latex] they can charge for [latex]n[/latex] shirts.
Solution

[latex]p(n)=-0.004n+34[/latex]

47. A phone company charges for service according to the formula: [latex]C(n)=24+0.1n[/latex], where [latex]n[/latex] is the number of minutes talked, and [latex]C(n)[/latex] is the monthly charge, in dollars. Find and interpret the rate of change and initial value.
48. A farmer finds there is a linear relationship between the number of bean stalks, [latex]n[/latex], she plants and the yield, [latex]y[/latex], each plant produces. When she plants [latex]30[/latex] stalks, each plant yields [latex]30[/latex] oz of beans. When she plants [latex]34[/latex] stalks, each plant produces [latex]28[/latex] oz of beans. Find a linear relationships in the form [latex]y=mn+b[/latex] that gives the yield when [latex]n[/latex] stalks are planted.
Solution

[latex]y=-0.5n+45[/latex]

49. A city’s population in the year 1960 was [latex]287\text{,}500[/latex]. In 1989 the population was [latex]275\text{,}900[/latex]. Compute the rate of growth of the population and make a statement about the population rate of change in people per year.
50. A town’s population has been growing linearly. In 2003, the population was [latex]45\text{,}000[/latex], and the population has been growing by [latex]1\text{,}700[/latex] people each year. Write an equation, [latex]P(t)[/latex], for the population [latex]t[/latex] years after 2003.
Solution

[latex]P(t)=1700t+45,000[/latex]

51. Suppose that average annual income (in dollars) for the years 1990 through 1999 is given by the linear function: [latex]I(x)=1054x+23\text{,}286[/latex], where [latex]x[/latex] is the number of years after 1990. Which of the following interprets the slope in the context of the problem?

a. As of 1990, average annual income was [latex]$23\text{,}286[/latex].
b. In the ten-year period from 1990–1999, average annual income increased by a total of [latex]$1\text{,}054[/latex].
c. Each year in the decade of the 1990s, average annual income increased by [latex]$1\text{,}054[/latex].
d. Average annual income rose to a level of [latex]$23\text{,}286[/latex] by the end of 1999.

52. When temperature is [latex]0[/latex] degrees Celsius, the Fahrenheit temperature is [latex]32[/latex]. When the Celsius temperature is [latex]100[/latex], the corresponding Fahrenheit temperature is [latex]212[/latex]. Express the Fahrenheit temperature as a linear function of [latex]C[/latex], the Celsius temperature, [latex]F(C)[/latex].

a. Find the rate of change of Fahrenheit temperature for each unit change temperature of Celsius.
b. Find and interpret [latex]F(28)[/latex].
c. Find and interpret [latex]F(–40)[/latex].

Solution

a. [latex]\text{Rate of change =}\frac{\Delta F}{\Delta C}=\frac{212-32}{100-0}=1.8\text{ degrees F for one degree change in C}[/latex]
b. [latex]F(28)=1.8(28)+32=82.4\text{ degrees F is 28 degrees C}[/latex]
c. [latex]F(-40)=1.8(-40)+32=-40\text{ degrees F is -40 degrees C}[/latex]

53. In 2004, a school population was [latex]1001[/latex]. By 2008 the population had grown to [latex]1697[/latex]. Assume the population is changing linearly.

a. How much did the population grow between the year 2004 and 2008?
b. How long did it take the population to grow from [latex]1001[/latex] students to [latex]1697[/latex] students?
c. What is the average population growth per year?
d. What was the population in the year 2000?
e. Find an equation for the population, [latex]P[/latex], of the school [latex]t[/latex] years after 2000.
f. Using your equation, predict the population of the school in 2011.

54. In 2003, a town’s population was [latex]1431[/latex]. By 2007 the population had grown to [latex]2134[/latex]. Assume the population is changing linearly.

a. How much did the population grow between the year 2003 and 2007?
b. How long did it take the population to grow from [latex]1431[/latex] people to [latex]2134[/latex] people?
c. What is the average population growth per year?
d. What was the population in the year 2000?
e. Find an equation for the population, [latex]P[/latex], of the town [latex]t[/latex] years after 2000.
f. Using your equation, predict the population of the town in 2014.

Solution

a. [latex]2134-1431=703[/latex] people
b. [latex]2007-2003=4[/latex] years
c. Average rate of growth [latex]=\frac{703}{4}=175.75[/latex] people per year. So, using [latex]y=mx+b[/latex], we have [latex]y=175.75x+1431[/latex].
d. The year 2000 corresponds to [latex]t=-3[/latex].
So, [latex]y=175.75(-3)+1431=903.75[/latex] or roughly [latex]904[/latex] people in year 2000
e. If the year 2000 corresponds to [latex]t=0[/latex], then we have ordered pair [latex](0,903.75)[/latex].
[latex]y=175.75x+903.75[/latex] corresponds to [latex]P(t)=175.75t+903.75[/latex].
f. The year 2014 corresponds to [latex]t=14[/latex]. Therefore, [latex]P(14)=175.75(14)+903.75=3364.25[/latex].
So, a population of 3364.

55. A phone company has a monthly cellular plan where a customer pays a flat monthly fee and then a certain amount of money per minute used on the phone. If a customer uses [latex]410[/latex] minutes, the monthly cost will be [latex]$71.50[/latex]. If the customer uses [latex]720[/latex] minutes, the monthly cost will be [latex]$118[/latex].

a. Find a linear equation for the monthly cost of the cell plan as a function of [latex]x[/latex], the number of monthly minutes used.
b. Interpret the slope and [latex]y[/latex]-intercept of the equation.
c. Use your equation to find the total monthly cost if [latex]687[/latex] minutes are used.

56. A phone company has a monthly cellular data plan where a customer pays a flat monthly fee of [latex]$10[/latex] and then a certain amount of money per megabyte (MB) of data used on the phone. If a customer uses [latex]20[/latex] MB, the monthly cost will be [latex]$11.20[/latex]. If the customer uses [latex]130[/latex] MB, the monthly cost will be [latex]$17.80[/latex].

a. Find a linear equation for the monthly cost of the data plan as a function of [latex]x[/latex], the number of MB used.
b. Interpret the slope and [latex]y[/latex]-intercept of the equation.
c. Use your equation to find the total monthly cost if [latex]250[/latex] MB are used.

Solution

a.

[latex]\begin{array}{l}\text{Ordered pairs are }(20,11.20)\text{ and }(130,17.80)\\\begin{array}{rcl}m&=&\frac{17.80-11.20}{130-20}=0.06\text{ and }b\text{ is at the point }(0,10)\\y&=&mx+b\\y&=& 0.06x+10\\\text{or }C(x)&=&0.06x+10 \end{array}\end{array}[/latex]

b.

[latex]0.06[/latex] – For every MB, the client is charged [latex]6[/latex] cents.
[latex](0,10)[/latex] – If no usage occurs, the client is charged [latex]$10[/latex].

c.

[latex]\begin{array}{rcl}C(250)&=& 0.06(250)+10\\&=&$25\end{array}[/latex]

57. In 1991, the moose population in a park was measured to be [latex]4\text{,}360[/latex]. By 1999, the population was measured again to be [latex]5\text{,}880[/latex]. Assume the population continues to change linearly.

a. Find a formula for the moose population, [latex]P[/latex] since 1990.
b. What does your model predict the moose population to be in 2003?

58. In 2003, the owl population in a park was measured to be [latex]340[/latex]. By 2007, the population was measured again to be [latex]285[/latex]. The population changes linearly. Let the input be years since 1990.

a. Find a formula for the owl population, [latex]P[/latex]. Let the input be years since 2003.
b. What does your model predict the owl population to be in 2012?

Solution

a.

[latex]\begin{array}{l}\text{Ordered pairs are }(0,340)\text{ and }(4,285)\\\begin{array}{rcl}m&=&\frac{285-340}{4-0}=-13.75\text{ and }b\text{ is at the point }(0,340)\\y&=&mx+b\\y&=&-13.75x+340 \\ \text{or }P(t)&=&-13.75t+340\hfill \end{array}\end{array}[/latex]

b.

[latex]\begin{array}{l}\text{The year 2012 corresponds to }t=9\\\begin{array}{rcl}P(9)&=&-13.75(9)+340\\&=&216.25\text{ or }216\text{ owls}\end{array}\end{array}[/latex]

59. The Federal Helium Reserve held about [latex]16[/latex] billion cubic feet of helium in 2010 and is being depleted by about [latex]2.1[/latex] billion cubic feet each year.

a. Give a linear equation for the remaining federal helium reserves, [latex]R[/latex], in terms of [latex]t[/latex], the number of years since 2010.
b. In 2015, what will the helium reserves be?
c. If the rate of depletion doesn’t change, in what year will the Federal Helium Reserve be depleted?

60. Suppose the world’s oil reserves in 2014 are [latex]1\text{,}820[/latex] billion barrels. If, on average, the total reserves are decreasing by [latex]25[/latex] billion barrels of oil each year:

a. Give a linear equation for the remaining oil reserves, [latex]R[/latex], in terms of [latex]t[/latex], the number of years since now.
b. Seven years from now, what will the oil reserves be?
c. If the rate at which the reserves are decreasing is constant, when will the world’s oil reserves be depleted?

Solution

a.

[latex]\begin{array}{l}\text{The year 2014 corresponds to }t=0.\\ \text{We have }m=-25\text{ and }b\text{ at the point }(0,1820)\\ \begin{array}{rcl}y&=&mx+b\\y&=&-25x+1820\\\text{or }R(t)&=&-25t+1820\end{array}\end{array}[/latex]

b.

[latex]\begin{array}{rcl}R(7)&=&-25(7)+1820\\ &=& 645\text{ billion cubic feet}\end{array}[/latex]

c.

[latex]\begin{array}{rcl}0&=&-25t+1820\\-1820&=&-25t\\72.8&=&t\;⇒\;2014+72.8=2086.8\text{. So, in the year 2086}\end{array}[/latex]

61. You are choosing between two different prepaid cell phone plans. The first plan charges a rate of [latex]26[/latex] cents per minute. The second plan charges a monthly fee of [latex]$19.95[/latex] plus [latex]11[/latex] cents per minute. How many minutes would you have to use in a month in order for the second plan to be preferable?
62. You are choosing between two different window washing companies. The first charges [latex]$5[/latex] per window. The second charges a base fee of [latex]$40[/latex] plus [latex]$3[/latex] per window. How many windows would you need to have for the second company to be preferable?
Solution

[latex]\begin{array}{l}\text{Plan 1: }y=5x\text{ where }x\text{ is number of windows}\\ \text{Plan 2: }y=3x+40\text{ where }x\text{ is number of windows}\\ \begin{array}{rcl}3x+40&\le&5x\\40&\le&2x\\20&\le&x\end{array}\\ \text{So, more than 20 windows}\end{array}[/latex]

63. When hired at a new job selling jewelry, you are given two pay options:

Option A: Base salary of [latex]$17\text{,}000[/latex] a year with a commission of [latex]12\%[/latex] of your sales
Option B: Base salary of [latex]$20\text{,}000[/latex] a year with a commission of [latex]5\%[/latex] of your sales

How much jewelry would you need to sell for option A to produce a larger income?

64. When hired at a new job selling electronics, you are given two pay options:

Option A: Base salary of [latex]$14\text{,}000[/latex] a year with a commission of [latex]10\%[/latex] of your sales
Option B: Base salary of [latex]$19\text{,}000[/latex] a year with a commission of [latex]4\%[/latex] of your sales

How many electronics would you need to sell for option A to produce a larger income?

Solution

[latex]\begin{array}{l}\text{Option A: }y=0.10x+14\text{,}000\text{ where }x\text{ is dollars of sales.}\\\text{Option B: }y=0.04x+19\text{,}000\text{ where }x\text{ is dollars of sales.}\\ \begin{array}{rcl}0.10x+14\text{,}000&\ge&0.04x+19\text{,}000\\0.06x+14\text{,}000&\ge&19\text{,}000\\0.06x&\ge&5\text{,}000\\x&\ge&83\text{,}333.33\end{array}\\\text{So, more than }$83\text{,}333.33\text{ in sales.}\end{array}[/latex]

65. When hired at a new job selling electronics, you are given two pay options:

Option A: Base salary of [latex]$20\text{,}000[/latex] a year with a commission of [latex]12\%[/latex] of your sales
Option B: Base salary of [latex]$26\text{,}000[/latex] a year with a commission of [latex]3\%[/latex] of your sales

How many electronics would you need to sell for option A to produce a larger income?

66. When hired at a new job selling electronics, you are given two pay options:

Option A: Base salary of [latex]$10\text{,}000[/latex] a year with a commission of [latex]9\%[/latex] of your sales
Option B: Base salary of [latex]$20\text{,}000[/latex] a year with a commission of [latex]4\%[/latex] of your sales

How much electronics would you need to sell for option A to produce a larger income?

Solution

[latex]\begin{array}{l}\text{Option A: }y=0.09x+10\text{,}000\text{ where }x\text{ is dollars of sales.}\\ \text{Option B: }y=0.04x+20\text{,}000\text{ where }x\text{ is dollars of sales.}\\ \begin{array}{rcl}0.09x+10\text{,}000&\ge&0.04x+20\text{,}000\\0.05x+10\text{,}000&\ge&20\text{,}000\\0.05x&\ge&10\text{,}000\\x&\ge& 200\text{,}000\end{array}\\ \text{So, more than }$200\text{,}000\text{ in sales.}\end{array}[/latex]

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Fanshawe Pre-Health Sciences Mathematics 1 Copyright © 2022 by Domenic Spilotro, MSc is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book