1.3 Integers
Learning Objectives
By the end of this section, you will be able to:
- Use negatives and opposites
- Simplify: expressions with absolute value
- Add integers
- Subtract integers
- Multiply integers
- Divide integers
- Simplify expressions with integers
- Evaluate variable expressions with integers
- Translate English phrases to algebraic expressions
- Use integers in applications
Use Negatives and Opposites
Our work so far has only included the counting numbers and the whole numbers. But if you have ever experienced a temperature below zero or accidentally overdrawn your checking account, you are already familiar with negative numbers. Negative numbers are numbers less than 0. The negative numbers are to the left of zero on the number line.
The number line shows the location of positive and negative numbers.
The arrows on the ends of the number line indicate that the numbers keep going forever. There is no biggest positive number, and there is no smallest negative number.
Is zero a positive or a negative number? Numbers larger than zero are positive, and numbers smaller than zero are negative. Zero is neither positive nor negative.
Consider how numbers are ordered on the number line. Going from left to right, the numbers increase in value. Going from right to left, the numbers decrease in value.
The numbers on a number line increase in value going from left to right and decrease in value going from right to left.
Remember that we use the notation:
[latex]a < b[/latex] (read “a is less than b”) when [latex]a[/latex] is to the left of [latex]b[/latex] on the number line.
[latex]a > b[/latex] (read “a is greater than b”) when [latex]a[/latex] is to the right of [latex]b[/latex] on the number line.
Now we need to extend the number line which showed the whole numbers to include negative numbers, too. The numbers marked by points in figure 1.3.1 are called the integers. The integers are the numbers {…}−3,−2,−1,0,1,2,3{…}
All the marked numbers are called integers.
Example 1.3.1
Order each of the following pairs of numbers, using < or >:
- [latex]14\underline{\hspace{0.5cm}}6[/latex]
- [latex]-1\underline{\hspace{0.5cm}}9[/latex]
- [latex]-1\underline{\hspace{0.5cm}}-4[/latex]
- [latex]2\underline{\hspace{0.5cm}}-20[/latex]

Solution
It may be helpful to refer to the number line shown.
a. 14 is to the right of 6 on the number line.
[latex]14\underline{\hspace{0.5cm}}6[/latex] [latex]14>6[/latex]
b. −1 is to the left of 9 on the number line.
[latex]−1\underline{\hspace{0.5cm}}9[/latex] [latex]−1<9[/latex]
c. −1 is to the right of −4 on the number line.
[latex]−1\underline{\hspace{0.5cm}}−4[/latex] [latex]−1>−4[/latex]
d. 2 is to the right of −20 on the number line.
[latex]2\underline{\hspace{0.5cm}}−20[/latex] [latex]2>−20[/latex]
Try It
1) Order each of the following pairs of numbers, using < or >:
- [latex]15\underline{\hspace{0.5cm}}7[/latex]
- [latex]−2\underline{\hspace{0.5cm}}5[/latex]
- [latex]−3\underline{\hspace{0.5cm}}−7[/latex]
- [latex]5\underline{\hspace{0.5cm}}−17[/latex]
Solution
- >
- <
- >
- >
2) Order each of the following pairs of numbers, using < or >:
- [latex]8\underline{\hspace{0.5cm}}13[/latex]
- [latex]3\underline{\hspace{0.5cm}}−4[/latex]
- [latex]−5\underline{\hspace{0.5cm}}−2[/latex]
- [latex]9\underline{\hspace{0.5cm}}−21[/latex]
Solution
- <
- >
- <
- >
You may have noticed that, on the number line, the negative numbers are a mirror image of the positive numbers, with zero in the middle. Because the numbers 2 and −2 are the same distance from zero, they are called opposites. The opposite of 2 is −2 and the opposite of −2 is 2.
Opposite
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
Figure 1.3.3 illustrates the definition.
The opposite of 3 is −3.

Sometimes in algebra, the same symbol has different meanings. Just like some words in English, the specific meaning becomes clear by looking at how it is used. You have seen the symbol “−” used in three different ways.
| [latex]10-4[/latex] | Between two numbers, it indicates the operation of subtraction. We read [latex]10-4[/latex] as ” 10 minus 4.” |
| [latex]-8[/latex] | In front of a number, it indicates a negative number. We read −8 as “negative eight.” |
| [latex]-x[/latex] | In front of a variable, it indicates the opposite. We read [latex]-x[/latex] as “the opposite of [latex]x[/latex].” |
| [latex]-(-2)[/latex] | Here there are two “−” signs. The one is the parentheses tells us the number is negative 2. and the one outside the parentheses tells us to take the opposite of −2. We read [latex]-(-2)[/latex] as “the opposite of negative two.” |
Opposite Notation
[latex]−a[/latex] means the opposite of the number [latex]a[/latex].
The notation [latex]−a[/latex] is read as “the opposite of [latex]a[/latex].”
Example 1.3.2
Find:
-
- the opposite of [latex]7[/latex]
- the opposite of [latex]−10[/latex]
- the opposite of [latex]-6[/latex]
Solution
a. [latex]-7[/latex] is the same distance from [latex]0[/latex] as [latex]7[/latex], but on the opposite side of [latex]0[/latex]
[latex]\xleftarrow[{-7\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}]{\overbrace{\;\;7\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}0\xrightarrow[{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;7}]{\overbrace{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;7}}[/latex]
The opposite of [latex]7[/latex] is [latex]−7[/latex].
b. [latex]10[/latex] is the same distance from [latex]0[/latex] as [latex]-10[/latex], but on the opposite side of [latex]0[/latex].
[latex]\xleftarrow[{-10\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}]{\overbrace{\;10\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}0\xrightarrow[{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;10}]{\overbrace{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;10}}[/latex]
The opposite of [latex]−10[/latex] is [latex]10[/latex].
c. [latex]-(-6)[/latex]
[latex]\xleftarrow[{-6\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}]{\overbrace{\;6\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}0\xrightarrow[{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;6}]{\overbrace{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;6}}[/latex]
The opposite of [latex]-(-6)[/latex] is [latex]-6[/latex].
Try It
3) Find:
- the opposite of [latex]4[/latex]
- the opposite of [latex]-3[/latex]
- [latex]-(-1)[/latex]
Solution
- [latex]-4[/latex]
- [latex]3[/latex]
- [latex]1[/latex]
4) Find:
- the opposite of [latex]8[/latex]
- the opposite of [latex]−5[/latex]
- [latex]-(-5)[/latex]
Solution
- [latex]-8[/latex]
- [latex]5[/latex]
- [latex]5[/latex]
Our work with opposites gives us a way to define the integers. The whole numbers and their opposites are called the integers. The integers are the numbers −3,−2,−1,0,1,2,3
Integers
The whole numbers and their opposites are called the integers.
The integers are the numbers −3,−2,−1,0,1,2,3
When evaluating the opposite of a variable, we must be very careful. Without knowing whether the variable represents a positive or negative number, we don’t know whether [latex]x[/latex] is positive or negative. We can see this in the below figure.
Example 1.3.3
Evaluate
- [latex]-x[/latex], when [latex]x=8[/latex]
- [latex]-x[/latex], when [latex]x=-8[/latex].
Solution
a.
To evaluate when [latex]x=8[/latex] means to substitute [latex]8[/latex] for [latex]x[/latex].
Step 1: Substitute [latex]8[/latex] for [latex]x[/latex].
[latex]-(8)[/latex]
Step 2: Write the opposite of [latex]8[/latex].
[latex]-8[/latex]
b.
To evaluate when [latex]x=-8[/latex] means to substitute [latex]-8[/latex] for [latex]x[/latex].
Step 1: Substitute [latex]-8[/latex] for [latex]x[/latex].
[latex]-(-8)[/latex]
Step 2: Write the opposite of [latex]-8[/latex].
[latex]8[/latex]
Try It
5) Evaluate [latex]-n[/latex] when
- [latex]n=4[/latex]
- [latex]n=-4[/latex]
Solution
- [latex]−4[/latex]
- [latex]4[/latex]
6) Evaluate [latex]-m[/latex] when
- [latex]m=11[/latex]
- [latex]m=-11[/latex]
Solution
- [latex]-11[/latex]
- [latex]11[/latex]
Simplify: Expressions with Absolute Value
We saw that numbers such as 2 and −2 are opposites because they are the same distance from 0 on the number line. They are both two units from 0. The distance between 0 and any number on the number line is called the absolute value of that number.
Absolute Value
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number [latex]n[/latex] is written as [latex]\left|n\right|[/latex].
For example,
- [latex]−5[/latex] is [latex]5[/latex] units away from [latex]0[/latex], so [latex]\left|−5\right|=5[/latex].
- 5 is 5 units away from 0, so [latex]\left|5\right|=5[/latex].
The figure below illustrates this idea. The integers 5 and −5 are 5 units away from 0.
[latex]\xleftarrow[{-5\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}]{\overbrace{\;5\;units\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}0\xrightarrow[{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;5}]{\overbrace{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;5units}}[/latex]
The absolute value of a number is never negative (because distance cannot be negative). The only number with absolute value equal to zero is the number zero itself, because the distance from 0 to 0 on the number line is zero units.
Property of Absolute Value
[latex]\left|n\right|\geq0[/latex] for all numbers
Absolute values are always greater than or equal to zero!
Mathematicians say it more precisely, “absolute values are always non-negative.” Non-negative means greater than or equal to zero.
Example 1.3.4
7) Simplify:
- [latex]\left|3\right|[/latex]
- [latex]\left|-44\right|[/latex]
- [latex]\left|0\right|[/latex]
Solution
The absolute value of a number is the distance between the number and zero. Distance is never negative, so the absolute value is never negative.
a. [latex]\left|3\right|=3[/latex]
b. [latex]\left|-44\right|=44[/latex]
c. [latex]\left|0\right|=0[/latex]
Try It
7) Simplify:
- [latex]\left|4\right|[/latex]
- [latex]\left|-28\right|[/latex]
- [latex]\left|0\right|[/latex]
Solution
- 4
- 28
- 0
8) Simplify:
- [latex]\left|-13\right|[/latex]
- [latex]\left|47\right|[/latex]
- [latex]\left|0\right|[/latex]
Solution
- 13
- 47
- 0
In the next example, we’ll order expressions with absolute values. Remember, positive numbers are always greater than negative numbers!
Example 1.3.5
Fill in [latex]<[/latex],[latex]>[/latex] or [latex]=[/latex] for each of the following pairs of numbers:
- [latex]\left|-5\right|\underline{\hspace{0.5cm}}-\left|-5\right|[/latex]
- [latex]8\underline{\hspace{0.5cm}}-\left|-8\right|[/latex]
- [latex]-9\underline{\hspace{0.5cm}}-\left|-9\right|[/latex]
- [latex]-\left(-16\right)\underline{\hspace{0.5cm}}\left|-16\right|[/latex]
Solution
a.
Step 1: Simplify.
[latex]-5\underline{\hspace{0.5cm}}--5[/latex]
Step 2: Order.
[latex]5>-5[/latex]
[latex]\left|5\right|>-\left|-5\right|[/latex]
b.
Step 1: Simplify.
[latex]8\underline{\hspace{0.5cm}}--8[/latex]
Step 2: Order.
[latex]8>-8[/latex]
[latex]\left|8\right|>-\left|-8\right|[/latex]
c.
Step 1: Simplify.
[latex]−9\underline{\hspace{0.5cm}}−−9[/latex]
Step 2: Order.
[latex]\begin{align*}-9&=-9\\\left|9\right|&=-\left|-9\right|\end{align*}[/latex]
d.
Step 1: Simplify.
[latex]--16\underline{\hspace{0.5cm}}-16|[/latex]
Step 2: Order.
[latex]16>−16[/latex]
[latex]−\left(−16\right)>−\left|-16\right|[/latex]
Try It
9) Fill in [latex]<[/latex], [latex]>[/latex], or [latex]=[/latex] for each of the following pairs of numbers:
- [latex]\left|-9\right|\underline{\hspace{0.5cm}}-\left|-9\right|[/latex]
- [latex]\left|2\right|\underline{\hspace{0.5cm}}-\left|-2\right|[/latex]
- [latex]\left|-8\right|\underline{\hspace{0.5cm}}\left|-8\right|[/latex]
- [latex]-\left(-9\right)\underline{\hspace{0.5cm}}-\left|-9\right|[/latex]
Solution
- >
- >
- <
- >
10) Fill in [latex]<[/latex], [latex]>[/latex], or [latex]=[/latex] for each of the following pairs of numbers:
- [latex]\left|7\right|\underline{\hspace{0.5cm}}-\left|-7\right|[/latex]
- [latex]-\left(-10\right)\underline{\hspace{0.5cm}}-\left|-10\right|[/latex]
- [latex]\left|-4\right|\underline{\hspace{0.5cm}}-\left|-4\right|[/latex]
- [latex]\left|-1\right|\underline{\hspace{0.5cm}}\left|-1\right|[/latex]
Solution
- >
- >
- >
- <
We now add absolute value bars to our list of grouping symbols. When we use the order of operations, first we simplify inside the absolute value bars as much as possible, then we take the absolute value of the resulting number.
Grouping Symbols
In the next example, we simplify the expressions inside absolute value bars first, just like we do with parentheses.
Example 1.3.6
Simplify: [latex]24-\left|19-3(6-2)\right|[/latex]
Solution
Step 1: Work inside parentheses first: subtract 2 from 6.
[latex]24-\left|19-3(4)\right|[/latex]
Step 2: Multiply 3(4).
[latex]24-\left|19-12\right|[/latex]
Step 3: Subtract inside the absolute value bars.
[latex]24-\left|7\right|[/latex]
Step 4: Take the absolute value.
[latex]24-7[/latex]
Step 5: Subtract
[latex]17[/latex]
Try It
11) Simplify: [latex]19-\left|11-4(3-1)\right|[/latex]
Solution
[latex]16[/latex]
12) Simplify: [latex]9-\left|8-4(7-5)\right|[/latex]
Solution
[latex]9[/latex]
Example 1.3.7
Evaluate:
- [latex]\left|x\right|[/latex] when [latex]x=-35[/latex]
- [latex]\left|-y\right|[/latex] when [latex]y=-20[/latex]
- [latex]-\left|u\right|[/latex] when [latex]u=12[/latex]
- [latex]-\left|p\right|[/latex] when [latex]p=-14[/latex]
Solution
a.
Step 1: Substitute [latex]-35[/latex]for [latex]x[/latex].
[latex]\left|-35\right|[/latex]
Step 2: Take the absolute value.
[latex]35[/latex]
b.
Step 1: Substitute [latex]-20[/latex] for [latex]y[/latex].
[latex] \left|-(-20)\right|[/latex]
Step 2: Simplify.
[latex]\left|20\right|[/latex]
Step 3: Take the absolute value.
[latex]20[/latex]
c.
Step 1: Substitute [latex]12[/latex] for [latex]u[/latex].
[latex]-\left|12\right|[/latex]
Step 2: Take the absolute value.
[latex]-12[/latex]
d.
Step 1: Substitute [latex]-14[/latex] for [latex]p[/latex].
[latex]-\left|-14\right|[/latex]
Step 2: Take the absolute value
[latex]-14[/latex]
Try It
13) Evaluate:
- [latex]\left|x\right|[/latex] when [latex]x=-17[/latex]
- [latex]\left|-y\right|[/latex] when [latex]y=39[/latex]
- [latex]-\left|m\right|[/latex] when [latex]m=22[/latex]
- [latex]-\left|p\right|[/latex] when [latex]p=-11[/latex].
Solution
- 17
- 39
- −22
- −11
14) Evaluate:
- [latex]\left|y\right|[/latex] when [latex]y=-23[/latex]
- [latex]\left|-y\right|[/latex] when [latex]y=-21[/latex]
- [latex]-\left|n\right|[/latex] when [latex]n=37[/latex]
- [latex]-\left|q\right|[/latex] when [latex]q=-49[/latex]
Solution
- 23
- 21
- −37
- −49
Add Integers
Most students are comfortable with the addition and subtraction facts for positive numbers. But doing addition or subtraction with both positive and negative numbers may be more challenging.
We will use two colour counters to model addition and subtraction of negatives so that you can visualize the procedures instead of memorizing the rules.
We let one colour (blue) represent positive. The other colour (red) will represent the negatives. If we have one positive counter and one negative counter, the value of the pair is zero. They form a neutral pair. The value of this neutral pair is zero.

We will use the counters to show how to add the four addition facts using the numbers 5,−5 and 3,−3.
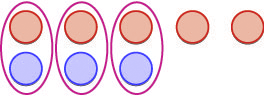
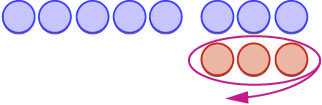
To add [latex]5+3[/latex], we realize that [latex]5+3[/latex] means the sum of 5 and 3.
| We start with 5 positives. |
 |
| And then we add 3 positives. |
 |
| We now have 8 positives. The sum of 5 and 3 is 8. |
 |
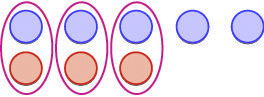
Now we will add [latex]-5+(-3)[/latex]. Watch for similarities to the last example [latex]5+3=8[/latex].
To add [latex]-5+(-3)[/latex], we realize this means the sum of −5 and −3.
| We start with 5 negatives. |
 |
| And then we add 3 negatives. |
 |
| We now have 8 negatives. The sum of −5 and −3 is −8. |
 |
In what ways were these first two examples similar?
- The first example adds 5 positives and 3 positives—both positives.
- The second example adds 5 negatives and 3 negatives—both negatives.
In each case we got 8—either 8 positives or 8 negatives.
When the signs were the same, the counters were all the same colour, and so we added them.

Example 1.3.8
Try It
15) Add:
- [latex]2+4[/latex]
- [latex]-2+(-4)[/latex]
Solution
- 6
- −6
16) Add:
- [latex]2+5[/latex]
- [latex]-2+(-5)[/latex]
Solution
- 7
- −7
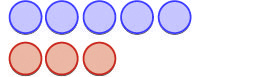
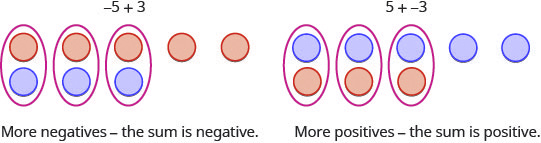
So what happens when the signs are different? Let’s add −5+3. We realize this means the sum of −5 and 3. When the counters were the same colour, we put them in a row. When the counters are a different colour, we line them up under each other.
Notice that there were more negatives than positives, so the result was negative.
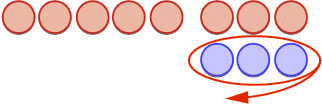
Let’s now add the last combination, [latex]5+(−3)[/latex].
When we use counters to model addition of positive and negative integers, it is easy to see whether there are more positive or more negative counters. So we know whether the sum will be positive or negative.
Example 1.3.9
Try It
17) Add:
- [latex]-2+4[/latex]
- [latex]2+(-4)[/latex]
Solution
- [latex]2[/latex]
- [latex]-2[/latex]
18) Add:
- [latex]-2+5[/latex]
- [latex]2+(-5)[/latex]
Solution
- [latex]3[/latex]
- [latex]-3[/latex]
Now that we have added small positive and negative integers with a model, we can visualize the model in our minds to simplify problems with any numbers.
When you need to add numbers such as [latex]37+(-53)[/latex], you really don’t want to have to count out 37 blue counters and 53 red counters. With the model in your mind, can you visualize what you would do to solve the problem?
Picture 37 blue counters with 53 red counters lined up underneath. Since there would be more red (negative) counters than blue (positive) counters, the sum would be negative. How many more red counters would there be? Because [latex]53-37=16[/latex], there are 16 more red counters.
Therefore, the sum of [latex]37+(-53)[/latex] is −16.
Let’s try another one. We’ll add [latex]-74+(−27)[/latex]. Again, imagine 74 red counters and 27 more red counters, so we’d have 101 red counters. This means the sum is −101.
Let’s look again at the results of adding the different combinations of 5,−5 and 3,−3.
Addition of Positive and Negative Integers
| [latex]5+3[/latex] | [latex]-5+(-3)[/latex] |
| [latex]8[/latex] | [latex]-8[/latex] |
| both positive, sum positive | both negative, sum negative |
When the signs are the same, the counters would be all the same colour, so add them.
| [latex]-5+3[/latex] | [latex]5+(-3)[/latex] |
| [latex]-2[/latex] | [latex]2[/latex] |
| different signs, more negatives, sum negative | different signs, more positives, sum positive |
When the signs are different, some of the counters would make neutral pairs, so subtract to see how many are left.
Visualize the model as you simplify the expressions in the following examples.
Example 1.3.10
Simplify
- [latex]19+(-47)[/latex]
- [latex]-14+(-36)[/latex]
Solution
a. Since the signs are different, we subtract 19 from 47. The answer will be negative because there are more negatives than positives.
Step 1: Subtract
[latex]19+(-47)[/latex]
[latex]-28[/latex]
b. Since the signs are the same, we add. The answer will be negative because there are only negatives.
Step 1: Add
[latex]-14+(-36)[/latex]
[latex]-50[/latex]
Try It
19) Simplify:
- [latex]-31+(-19)[/latex]
- [latex]15+(-32)[/latex]
Solution
- [latex]-50[/latex]
- [latex]-17[/latex]
20) Simplify:
- [latex]-42+(-28)[/latex]
- [latex]25+(-61)[/latex]
Solution
- [latex]-70[/latex]
- [latex]-36[/latex]
The techniques used up to now extend to more complicated problems, like the ones we’ve seen before. Remember to follow the order of operations!
Example 1.3.11
Simplify: [latex]-5+3(-2+7)[/latex]
Solution
Step 1: Simplify inside the parentheses.
[latex]-5+3(5)[/latex]
Step 2: Multiply.
[latex]-5+15[/latex]
Step 3: Add left to right.
[latex]10[/latex]
Try It
21) Simplify: [latex]-2+5(-4+7)[/latex]
Solution
13
22) Simplify: [latex]-4+2(-3+5)[/latex]
Solution
0
Subtract Integers
We will continue to use counters to model subtraction. Remember, the blue counters represent positive numbers and the red counters represent negative numbers.
Perhaps when you were younger, you read “5−3” as “5 take away 3”. When you use counters, you can think of subtraction the same way!
We will model the four subtraction facts using the numbers 5 and 3.
[latex]5-3[/latex] [latex]-5-(-3)[/latex] [latex]-5-3[/latex] [latex]5-(-3)[/latex]
To subtract 5-3, we restate the problem as “5 takes away 3”.
| We start with 5 positives. |
|
| We ‘take away’ 3 positives. |
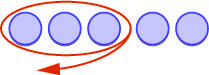 |
| We have 2 positives left. | The difference of 5 and 3 is 2. |
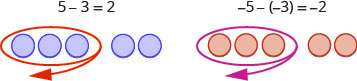
Now we will subtract [latex]-5-(-3)[/latex]. Watch for similarities to the last example [latex]5-3=2[/latex].
To subtract [latex]-5-(-3)[/latex], we restate this as “−5 take away −3”.
| We start with 5 negatives. |
|
| We ‘take away’ 3 negatives. |
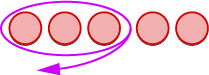 |
| We have 2 negatives left. | The difference of −5 and −3 is −2. |
Notice that these two examples are much alike: The first example, we subtract 3 positives from 5 positives and end up with 2 positives.
In the second example, we subtract 3 negatives from 5 negatives and end up with 2 negatives.
Each example used counters of only one colour, and the “take away” model of subtraction was easy to apply.
Example 1.3.12
Subtract:
- [latex]7-5[/latex]
- [latex]-7-(-5)[/latex]
Solution
a.
Step 1: Take 5 positive from 7 positives and get 2 positives.
[latex]7-5=2[/latex]
b.
Step 1: Take 5 negatives from 7 negatives and get 2 negatives.
[latex]-7-(-5)=-2[/latex]
Try It
23) Subtract:
- [latex]6-4[/latex]
- [latex]-6-(-4)[/latex]
Solution
- [latex]2[/latex]
- [latex]-2[/latex]
24) Subtract:
- [latex]7-4[/latex]
- [latex]-7-(-4)[/latex]
Solution
- [latex]3[/latex]
- [latex]-3[/latex]
What happens when we have to subtract one positive and one negative number? We’ll need to use both white and red counters as well as some neutral pairs. Adding a neutral pair does not change the value. It is like changing quarters to nickels—the value is the same, but it looks different.
- To subtract [latex]-5-3[/latex], we restate it as −5 take away 3.
We start with 5 negatives. We need to take away 3 positives, but we do not have any positives to take away.
Remember, a neutral pair has value zero. If we add 0 to 5 its value is still 5. We add neutral pairs to the 5 negatives until we get 3 positives to take away.
And now, the fourth case, [latex]5-(-3)[/latex]. We start with 5 positives. We need to take away 3 negatives, but there are no negatives to take away. So we add neutral pairs until we have 3 negatives to take away.
Example 1.3.13
Subtract:
- [latex]-3-1[/latex]
- [latex]3-(-1)[/latex].
Try It
25) Subtract:
- [latex]-6-4[/latex]
- [latex]6-(-4)[/latex]
Solution
- [latex]-10[/latex]
- [latex]10[/latex]
26) Subtract:
- [latex]-7-4[/latex]
- [latex]7-(-4)[/latex]
Solution
- [latex]-11 [/latex]
- [latex]11[/latex]
Have you noticed that subtraction of signed numbers can be done by adding the opposite? In example 1.3.13 (above), [latex]-3-1[/latex] is the same as [latex]-3+(-1)[/latex] and [latex]3-(-1)[/latex] is the same as [latex]3+1[/latex]. You will often see this idea, the subtraction property, written as follows:
Subtraction Property
Subtracting a number is the same as adding its opposite.
Look at these two examples.
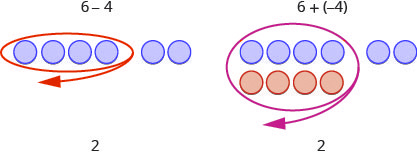
Of course, when you have a subtraction problem that has only positive numbers, like [latex]6-4[/latex], you just do the subtraction. You already knew how to subtract [latex]6-4[/latex] long ago. But knowing that [latex]6-4[/latex] gives the same answer as [latex]6+(-4)[/latex] helps when you are subtracting negative numbers. Make sure that you understand how [latex]6-4[/latex] and [latex]6+(-4)[/latex] give the same results!
Example 1.3.14
Simplify:
- [latex]13-8[/latex] and [latex]13+(-8)[/latex]
- [latex]-17-9[/latex] and [latex]-17+(-9)[/latex]
Solution
a.
Step 1: Subtract.
[latex]\begin{align*}13-8&=5\\13+(-8)&=5\end{align*}[/latex]
b.
Step 1: Subtract.
[latex]\begin{align*}-17-9&=-26\\-17+(-9)&=-26\end{align*}[/latex]
Try It
27) Simplify:
- [latex]21-13[/latex] and [latex]21+(-13)[/latex]
- [latex]-11-7[/latex] and [latex]-11+(-7)[/latex].
Solution
- [latex]8[/latex]
- [latex]−18[/latex]
28) Simplify:
- [latex]15-7[/latex] and [latex]15+(-7)[/latex]
- [latex]-14-8[/latex] and [latex]-14+(-8)[/latex].
Solution
- [latex]8[/latex]
- [latex]-22[/latex]
Look at what happens when we subtract a negative.

Subtracting a negative number is like adding a positive!
You will often see this written as [latex]a-b=a+b[/latex].
Does that work for other numbers, too? Let’s do the following example and see.
Example 1.3.15
Simplify:
- [latex]9-(-15)[/latex] and [latex]9+15[/latex]
- [latex]-7-(-4)[/latex] and [latex]-7+4[/latex]
Solution
a.
Step 1: Subtract.
[latex]\begin{align*}9-(-15)&=24\\9+15&=24\end{align*}[/latex]
b.
Step 1: Subtract.
[latex]\begin{align*}-7-(-4)&=-3\\-7+4&=-3\end{align*}[/latex]
Try It
29) Simplify
- [latex]6-(-13)[/latex] and [latex]6+13[/latex]
- [latex]-5-(-1)[/latex] and [latex]-5+1[/latex]
Solution
- [latex]19[/latex]
- [latex]-4[/latex]
30) Simplify:
- [latex]4-(-19)[/latex] and [latex]4+19[/latex]
- [latex]-4-(-7)[/latex] and [latex]-4+7[/latex]
Solution
- [latex]23[/latex]
- [latex]3[/latex]
Let’s look again at the results of subtracting the different combinations of 5,−5 and 3,−3.
Subtraction of Integers
|
[latex]5-3[/latex] [latex]2[/latex] 5 positives take 3 positives 2 positives |
[latex]-5-(-3)[/latex] [latex]-2[/latex] 5 negatives take away 3 negatives 2 negatives |
When there would be enough counters of the colour to take away, subtract.
|
[latex]-5-3[/latex] [latex]-8[/latex] 5 negatives, want to take away 3 positives need neutral pairs |
[latex]5-(-3)[/latex] [latex]8[/latex] 5 positives, want to take away 3 negatives need neutral pairs |
When there would be not enough counters of the colour to take away, add.
What happens when there are more than three integers? We just use the order of operations as usual.
Example 1.3.16
Simplify: [latex]7-(-4-3)-9[/latex]
Solution
Step 1: Simplify inside the parentheses first.
[latex]7-(-7)-9[/latex]
Step 2: Subtract left to right
[latex]14-9[/latex]
Step 3: Subtract
[latex]5[/latex]
Try It
31) Simplify: [latex]8-(-3-1)-9[/latex]
Solution
[latex]3[/latex]
32) Simplify: [latex]12-(-9-6)-14[/latex]
Solution
[latex]13[/latex]
Multiply Integers
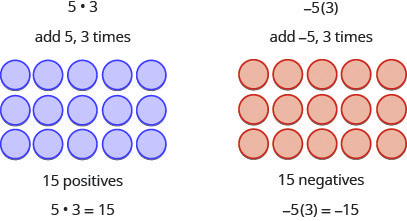
Since multiplication is mathematical shorthand for repeated addition, our model can easily be applied to show multiplication of integers. Let’s look at this concrete model to see what patterns we notice. We will use the same examples that we used for addition and subtraction. Here, we will use the model just to help us discover the pattern.
We remember that [latex]a\times b[/latex] means add [latex]a[/latex], [latex]b[/latex] times. Here, we are using the model just to help us discover the pattern.
The next two examples are more interesting.
What does it mean to multiply 5 by −3? It means subtract 5, 3 times. Looking at subtraction as “taking away,” it means to take away 5, 3 times. But there is nothing to take away, so we start by adding neutral pairs on the workspace. Then we take away 5 three times.
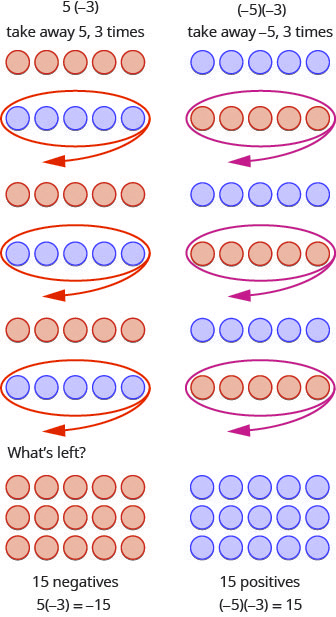
In summary:
| [latex]5\times3=15[/latex]
[latex]5\times-3=-15[/latex] |
[latex]-5\times3=-15[/latex]
[latex]-5\times-3=15[/latex] |
Notice that for multiplication of two signed numbers, when the:
- signs are the same, the product is positive.
- signs are different, the product is negative.
We’ll put this all together in the chart below.
Multiplication of Signed Numbers
For multiplication of two signed numbers:
| Same signs | Product | Example |
|---|---|---|
| Two positives Two negatives |
Positive Positive |
[latex]7\times4=28[/latex] [latex]-8\times-6=48[/latex] |
If the signs are the same, the result is positive.
| Different signs | Product | Example |
|---|---|---|
| Positive and negative Negative and positive |
Negative Negative |
[latex]7\times-9=-63[/latex] [latex]-5\times10=-50[/latex] |
Example 1.3.17
- [latex]9\times3[/latex]
- [latex]-2(-5)[/latex]
- [latex]4(-8)[/latex]
- [latex]7\times6[/latex]
Solution
a.
Step 1: Multiply, noting that the signs are different so the product is negative.
[latex]9\times3=-27[/latex]
b.
Step 1: Multiply, noting that the signs are the same so the product is positive.
[latex]-2(-5)=10[/latex]
c.
Step 1: Multiply, with different signs.
[latex]4(-8)=-32[/latex]
d.
Step 1: Multiply, with same signs.
[latex]7\times6=42[/latex]
Try It
33) Multiply:
- [latex]-6\times8[/latex]
- [latex]-4(-7)[/latex]
- [latex]9(-7)[/latex]
- [latex]5\times12[/latex]
Solution
- [latex]-48[/latex]
- [latex]28[/latex]
- [latex]-63[/latex]
- [latex]60[/latex]
34) Multiply:
- [latex]-8\times7[/latex]
- [latex]-6(-9)[/latex]
- [latex]7(-4)[/latex]
- [latex]3\times13[/latex]
Solution
- [latex]-56[/latex]
- [latex]54[/latex]
- [latex]-28[/latex]
- [latex]39[/latex]
When we multiply a number by 1, the result is the same number. What happens when we multiply a number by −1. Let’s multiply a positive number and then a negative number by −1 to see what we get.
Each time we multiply a number by −1, we get its opposite!
Multiplying a number by −1 gives its opposite.
Example 1.3.18
Multiply:
- [latex]-1\times7[/latex]
- [latex]-1(-11)[/latex]
Solution
a.
Step 1: Multiply, noting that the signs are different so the product is negative.
[latex]-1\times7=-7[/latex]
[latex]-7[/latex] is the opposite of [latex]7[/latex].
b.
Step 1: Multiply, noting that the signs are the same so the product is positive.
[latex]-1(-11)=11[/latex]
[latex]11[/latex] is the opposite of [latex]-11[/latex].
Try It
35) Multiply:
- [latex]-1\times9[/latex]
- [latex]-1(-17)[/latex]
Solution
- [latex]-9[/latex]
- [latex]17[/latex]
36) Multiply:
- [latex]-1\times8[/latex]
- [latex]-1(-16)[/latex]
Solution
- [latex]-8[/latex]
- [latex]16[/latex]
Divide Integers
What about division? Division is the inverse operation of multiplication. So, [latex]15\div3=5[/latex] because [latex]5\times3=15[/latex] In words, this expression says that 15 can be divided into three groups of five each because adding five three times gives 15. Look at some examples of multiplying integers, to figure out the rules for dividing integers.
Division follows the same rules as multiplication!
For division of two signed numbers, when the:
- signs are the same, the quotient is positive.
- signs are different, the quotient is negative.
And remember that we can always check the answer of a division problem by multiplying.
Multiplication and Division of Signed Numbers
For multiplication and division of two signed numbers:
- If the signs are the same, the result is positive.
- If the signs are different, the result is negative.
| Same signs | Result |
|---|---|
| Two positives Two negatives |
Positive Positive |
| If the signs are the same, the result is positive. | |
| Different signs | Result |
|---|---|
| Positive and negative Negative and positive |
Negative Negative |
| If the signs are different, the result is negative. | |
Example 1.3.19
Divide:
- [latex](-27)\div3[/latex]
- [latex]-100\div(-4)[/latex]
Solution
a.
Step 1: Divide. With different signs, the quotient is negative.
[latex]-27\div3=-9[/latex]
b.
Step 1: Divide. With signs that are the same, the quotient is positive.
[latex]-100\div(-4)= 25[/latex]
Try It
37) Divide:
- [latex]-42\div6[/latex]
- [latex]-117\div-3[/latex]
Solution
- [latex]-7[/latex]
- [latex]39[/latex]
38) Divide:
- [latex]-63\div7[/latex]
- [latex]-115\div-5[/latex]
Solution
- [latex]-9[/latex]
- [latex]23[/latex]
Simplify Expressions with Integers
What happens when there are more than two numbers in an expression? The order of operations still applies when negatives are included. Remember My Dear Aunt Sally?
Let’s try some examples. We’ll simplify expressions that use all four operations with integers—addition, subtraction, multiplication, and division. Remember to follow the order of operations.
Example 1.3.20
Simplify: [latex]7(-2)+4(-7)-6[/latex].
Solution
Step 1: Multiply first.
[latex]-14+(-28)-6[/latex]
Step 2: Add.
[latex]-42-6[/latex]
Step 3: Subtract.
[latex]-48[/latex]
Try It
Solution
[latex]-63[/latex]
40) Simplify: [latex]9(-3)+7(-8)-1[/latex]
Solution
[latex]-84[/latex]
Example 1.3.21
Simplify:
- [latex](-2)^4[/latex]
- [latex]-2^4[/latex]
Solution
a.
Step 1: Write in expanded from.
[latex](-2)(-2)(-2)(-2)[/latex]
Step 2: Multiply.
[latex]4(-2)(-2)[/latex]
Step 3: Multiply.
[latex]-8(-2)[/latex]
Step 4: Multiply.
[latex]16[/latex]
b.
Step 1: Write in expanded form. We are asked to find the opposite of [latex]2^4[/latex].
[latex]-(2\times2\times2\times2)[/latex]
Step 2: Multiply.
[latex]-(4\times2\times2)[/latex]
Step 3: Multiply.
[latex]-(8\times2)=-16[/latex]
Notice the difference in parts a and b. In part a, the exponent means to raise what is in the parentheses, the (−2) to the 4th power. In part b, the exponent means to raise just the 2 to the 4th power and then take the opposite.
Try It
41) Simplify:
- [latex](-3)^4[/latex]
- [latex]-3^4[/latex]
Solution
- 81
- −81
42) Simplify:
- [latex](-7)^2[/latex]
- [latex]-7^2[/latex]
Solution
- 49
- −49
The next example reminds us to simplify inside parentheses first.
Example 1.3.22
Simplify: [latex]12-3(9-12)[/latex]
Solution
Step 1: Subtract in parentheses first.
[latex]12-3(-3)[/latex]
Step 2: Multiply.
[latex]12-(-9)[/latex]
Step 3: Subtract.
[latex]21[/latex]
Try It
43) Simplify: [latex]17-4(8-11)[/latex]
Solution
[latex]29[/latex]
44) Simplify: [latex]16-6(7-13)[/latex]
Solution
[latex]52[/latex]
Example 1.3.23
Simplify: [latex]8(-9)\div(-2)^3[/latex]
Solution
Step 1: Exponents first.
[latex]8(-9)\div(-8)[/latex]
Step 2: Multiply
[latex]-72\div-8[/latex]
Step 3: Divide.
[latex]9[/latex]
Try It
45) Simplify: [latex]12(-9)\div(-3)^3[/latex]
Solution
[latex]4[/latex]
46) Simplify: [latex]18(-4)\div(-2)^3[/latex]
Solution
[latex]9[/latex]
Example 1.3.24
Simplify: [latex]-30\div+2+(-3)(-7)[/latex]
Solution
Step 1: Multiply and divide left to right, so divide first.
[latex]-15+(-3)(-7)[/latex]
Step 2: Add.
[latex]-15+21=6[/latex]
Try It
47) Simplify [latex]-27\div3+(-5)(-6)[/latex]
Solution
[latex]21[/latex]
48) Simplify [latex]-32\div4+(-2)(-7)[/latex]
Solution
[latex]6[/latex]
Evaluate Variable Expressions with Integers
Remember that to evaluate an expression means to substitute a number for the variable in the expression. Now we can use negative numbers as well as positive numbers.
Example 1.3.25
When [latex]n=-5[/latex], evaluate:
- [latex]n+1[/latex]
- [latex]-n+1[/latex]
Solution
a.
Step 1: Substitute [latex]-5[/latex] for [latex]n[/latex].
[latex]-5+1[/latex]
Step 2: Simplify.
[latex]-4[/latex]
b.
Step 1: Substitute [latex]-5[/latex] for [latex]n[/latex].
[latex]-(-5)+1[/latex]
Step 2: Simplify.
[latex] 5+1[/latex]
Step 3: Add.
[latex]6[/latex]
Try It
49) When [latex]n=-8[/latex], evaluate
- [latex]n+2[/latex]
- [latex]-n+2[/latex]
Solution
- [latex]-6[/latex]
- [latex]10[/latex]
50) When [latex]y=-9[/latex], evaluate
- [latex]y+8[/latex]
- [latex]-y+8[/latex].
Solution
- [latex]-1[/latex]
- [latex]17[/latex]
Example 1.3.26
Evaluate [latex](x+y)^2[/latex] when [latex]x=-18[/latex] and [latex]y=24[/latex].
Solution
Step 1: Substitute [latex]-18[/latex] for [latex]x[/latex] and [latex]24[/latex] for [latex]y[/latex].
[latex](-18+24)^2[/latex]
Step 2: Add inside parentheses.
[latex](6)^2[/latex]
Step 3: Simplify.
[latex]36[/latex]
Try It
51) Evaluate [latex](x+y)^2[/latex] when [latex]x=-15[/latex] and [latex]y=29[/latex]
Solution
[latex]196[/latex]
52) Evaluate [latex](x+y)^3[/latex] when [latex]x=-8[/latex] and [latex]y=10[/latex]
Solution
[latex]8[/latex]
Example 1.3.27
Evaluate [latex]20-z[/latex] when
- [latex]z=12[/latex]
- [latex]z=-12[/latex]
Solution
a.
Step 1: Substitute [latex]12[/latex] for [latex]z[/latex].
[latex]20-12[/latex]
Step 2: Subtract.
[latex]8[/latex]
b.
Step 1: Substitute [latex]-12[/latex] for [latex]z[/latex].
[latex]20-(-12)[/latex]
Step 2: Subtract.
[latex]32[/latex]
Try It
53) Evaluate: [latex]17-k[/latex] when
- [latex]k=19[/latex]
- [latex]k=-19[/latex]
Solution
- [latex]-2[/latex]
- [latex]36[/latex]
54) Evaluate: [latex]-5-b[/latex] when
- [latex]b=14[/latex]
- [latex]b=-14[/latex]
Solution
- [latex]-19[/latex]
- [latex]9[/latex]
Example 1.3.28
Evaluate: [latex]2x^2+3x+8[/latex] when [latex]x=4[/latex].
Solution
Substitute [latex]4[/latex] for [latex]x[/latex]. Use parentheses to show multiplication.
Step 1: Substitute.
[latex]2(4)^2+3(4)+8[/latex]
Step 2: Evaluate exponents.
[latex]2(16)+3(4)+8[/latex]
Step 3: Multiply.
[latex]32+12+8[/latex]
Step 4: Add.
[latex]52[/latex]
Try It
55) Evaluate: [latex]3x^2-2x+6[/latex] when [latex]x=-3[/latex].
Solution
[latex]39[/latex]
56) Evaluate: [latex]4x^2-x-5[/latex] when [latex]x=-2[/latex].
Solution
[latex]13[/latex]
Translate Phrases to Expressions with Integers
Our earlier work translating English to algebra also applies to phrases that include both positive and negative numbers.
Example 1.3.29
Translate and simplify: the sum of [latex]8[/latex] and [latex]-12[/latex], increased by [latex]3[/latex].
Solution
Step 1: Translate.
[latex][8+(-12)]+3[/latex]
Step 2: Simplify. Be careful not to confuse the brackets with an absolute value sign.
[latex](-4)+3[/latex]
Step 3: Add.
[latex]-1[/latex]
Try It
57) Translate and simplify the sum of [latex]9[/latex] and [latex]-16[/latex], increased by [latex]4[/latex].
Solution
[latex](9-16)+4=3[/latex]
58) Translate and simplify the sum of [latex]-8[/latex] and [latex]-12[/latex], increased by [latex]7[/latex].
Solution
[latex](-8-12)+7=-13[/latex]
When we first introduced the operation symbols, we saw that the expression may be read in several ways. They are listed below.
- [latex]a-b[/latex]
- [latex]a[/latex] minus [latex]b[/latex]
- the difference of [latex]a[/latex] and [latex]b[/latex]
- [latex]b[/latex] subtracted from [latex]a[/latex]
- [latex]b[/latex] less than [latex]a[/latex]
Be careful to get [latex]a[/latex] and [latex]b[/latex] in the right order!
Example 1.3.30
Translate and then simplify
- The difference of [latex]13[/latex] and [latex]-21[/latex]
- Subtract [latex]24[/latex] from [latex]-19[/latex]
Solution
a.
Step 1: Translate.
[latex]13-(-21)[/latex]
Step 2: Simplify.
[latex]34[/latex]
b.
Step 1: Translate. Remember, “subtract [latex]b[/latex] from [latex]a[/latex]” means [latex]a-b[/latex].
[latex]-19-24[/latex]
Step 2: Simplify.
[latex]-43[/latex]
Try It
59) Translate and simplify
- the difference of [latex]14[/latex] and [latex]-23[/latex]
- subtract [latex]21[/latex] from [latex]-17[/latex]
Solution
- [latex]14-(-23)=37[/latex]
- [latex]-17-21=-38[/latex]
60) Translate and simplify
- the difference of [latex]11[/latex] and [latex]-19[/latex]
- subtract [latex]18[/latex] from [latex]-11[/latex].
Solution
- [latex]11-(-19)=30[/latex]
- [latex]-11-18=-29[/latex]
Once again, our prior work translating English to algebra transfers to phrases that include both multiplying and dividing integers. Remember that the keyword for multiplication is “product” and for division is “quotient.”
Example 1.3.31
Translate to an algebraic expression and simplify if possible: the product of [latex]-2[/latex] and [latex]14[/latex].
Solution
Step 1: Translate.
[latex](-2)(14)[/latex]
Step 2: Simplify.
[latex]-28[/latex]
Try It
61) Translate to an algebraic expression and simplify if possible: the product of [latex]-5[/latex] and [latex]12[/latex].
Solution
[latex]-5(12)=-60[/latex]
62) Translate to an algebraic expression and simplify if possible: the product of [latex]8[/latex] and [latex]-13[/latex].
Solution
[latex]8(-13)=-104[/latex]
Example 1.3.32
Translate to an algebraic expression and simplify if possible: the quotient of [latex]-56[/latex] and [latex]-7[/latex].
Solution
Step 1: Translate.
[latex]-56 \div -7[/latex]
Step 2: Simplify.
[latex]8[/latex]
Try It
63) Translate to an algebraic expression and simplify if possible: the quotient of [latex]-63[/latex] and [latex]-9[/latex].
Solution
[latex]-63\div -9=7[/latex]
64) Translate to an algebraic expression and simplify if possible: the quotient of [latex]-72[/latex] and [latex]-9[/latex].
Solution
[latex]-72\div -9=8[/latex]
Use Integers in Applications
We’ll outline a plan to solve applications. It’s hard to find something if we don’t know what we’re looking for or what to call it! So when we solve an application, we first need to determine what the problem is asking us to find. Then we’ll write a phrase that gives the information to find it. We’ll translate the phrase into an expression and then simplify the expression to get the answer. Finally, we summarize the answer in a sentence to make sure it makes sense.
How to Apply a Strategy to Solve Applications with Integers
Example 1.3.33
The temperature in Urbana, Illinois one morning was [latex]11[/latex] degrees. By mid-afternoon, the temperature had dropped to [latex]−9[/latex] degrees. What was the difference of the morning and afternoon temperatures?
Solution
Step 1: Read the problem. Make sure all the words and ideas are understood.
Step 2: Identify what we are asked to find.
The difference of the morning and afternoon temperatures.
Step 3: Write a phrase that gives the information to find it.
The difference of [latex]11[/latex] and [latex]−9[/latex].
Step 4: Translate the phrase to an expression.
[latex]11-(-9)[/latex]
Step 5: Simplify the expression.
[latex]20[/latex]
Step 6: Write a complete sentence that answers the question.
The difference in temperatures was 20 degrees.
Try It
65) The temperature in Anchorage, Alaska one morning was [latex]15[/latex] degrees. By mid-afternoon the temperature had dropped to [latex]30[/latex] degrees below zero. What was the difference in the morning and afternoon temperatures?
Solution
The difference in temperatures was [latex]45[/latex] degrees.
66) The temperature in Denver was [latex]-6[/latex] degrees at lunchtime. By sunset the temperature had dropped to [latex]-15[/latex] degrees. What was the difference in the lunchtime and sunset temperatures?
Solution
The difference in temperatures was [latex]9[/latex] degrees.
HOW TO
Apply a Strategy to Solve Applications with Integers.
- Read the problem. Make sure all the words and ideas are understood
- Identify what we are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Answer the question with a complete sentence.
Example 1.3.34
The Mustangs football team received three penalties in the third quarter. Each penalty gave them a loss of fifteen yards. What is the number of yards lost?
Solution
Step 1: Read the problem. Make sure all the words and ideas are understood.
Step 2: Identify what we are asked to find.
The number of yards lost.
Step 3: Write a phrase that gives the information to find it.
Three times a [latex]15[/latex]-yard penalty.
Step 4: Translate the phrase to an expression.
[latex]3(-15)[/latex]
Step 5: Simplify the expression.
[latex]-45[/latex]
Step 6: Answer the question with a complete sentence.
The team lost [latex]45[/latex] yards.
Try It
67) The Bears played poorly and had seven penalties in the game. Each penalty resulted in a loss of [latex]15[/latex] yards. What is the number of yards lost due to penalties?
Solution
The Bears lost [latex]105[/latex] yards.
68) Bill uses the ATM on campus because it is convenient. However, each time he uses it he is charged a $2 fee. Last month he used the ATM eight times. How much was his total fee for using the ATM?
Solution
A $16 fee was deducted from his checking account.
Key Concepts
- Multiplication and Division of Two Signed Numbers
- Same signs—Product is positive
- Different signs—Product is negative
- Strategy for Applications
- Identify what you are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Answer the question with a complete sentence
- Addition of Positive and Negative Integers
| [latex]5+3=8[/latex] both positive, sum positive |
[latex]-5+(-3)=-8[/latex] both negative, sum negative |
| [latex]-5+3=-2[/latex] different signs, more negatives sum negative |
[latex]5+(-3)=2[/latex] different signs, more positives sum positive |
- Property of Absolute Value: [latex]\left|n\right|\geq0[/latex] for all numbers. Absolute values are always greater than or equal to zero!
- Subtraction of Integers
| [latex]5-3=2[/latex] 5 positives take away 3 positives 2 positive |
[latex]-5-(-3)=-2[/latex] 5 negatives, take away 3 negatives 2 negatives |
| [latex]-5-3=-8[/latex] 5 negatives, want to subtract 3 positives need neutral pairs |
[latex]5-(-3)=2[/latex] 5 positives, want to subtract 3 negatives need neutral pairs |
- Subtraction Property: Subtracting a number is the same as adding its opposite.
- Multiplication and Division of Two Signed Numbers
- Same signs—Product is positive
- Different signs—Product is negative
- Strategy for Applications
-
-
- Identify what you are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Answer the question with a complete sentence.
-
Self Check
After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Glossary
- absolute value
- The absolute value of a number is its distance from 0 on the number line. The absolute value of a number [latex]n[/latex] is written as [latex]\left|n\right|[/latex].
- integers
- The whole numbers and their opposites are called the integers: …−3, −2, −1, 0, 1, 2, 3…
- opposite
- The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero: [latex]−a[/latex] means the opposite of the number [latex]a[/latex]. The notation [latex]−a[/latex] is read as “the opposite of [latex]a[/latex].
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero: -a means the opposite of the number. The notation -a is read “the opposite of a.”
The whole numbers and their opposites are called the integers: ...−3, −2, −1, 0, 1, 2, 3...
The absolute value of a number is its distance from 0 on the number line. The absolute value of a number n is written as |n|.