1.4 Fractions

 Learning Objectives

By the end of this section, you will be able to:

  • Find equivalent fractions
  • Simplify fractions
  • Multiply fractions
  • Divide fractions
  • Simplify expressions written with a fraction bar
  • Translate phrases to expressions with fractions
  • Add or subtract fractions with a common denominator
  • Add or subtract fractions with different denominators
  • Use the order of operations to simplify complex fractions
  • Evaluate variable expressions with fractions

Find Equivalent Fractions

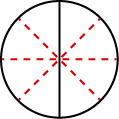
Fractions are a way to represent parts of a whole. The fraction [latex]\frac13[/latex] means that one whole has been divided into 3 equal parts and each part is one of the three equal parts. See (Figure 1.4.1). The fraction [latex]\frac23[/latex] represents two of three equal parts. In the fraction [latex]\frac23[/latex] the 2 is called the numerator and the 3 is called the denominator.

The circle on the left has been divided into 3 equal parts. Each part is [latex]\frac13[/latex] of the 3 equal parts. In the circle on the right, [latex]\frac23[/latex] of the circle is shaded (2 of the 3 equal parts).

Two circles are shown, each divided into three equal pieces by lines. The left hand circle is labeled “one third” in each section. Each section is shaded. The circle on the right is shaded in two of its three sections.
Figure 1.4.1. The circle on the left has been divided into 3 equal parts. Each part is 1/3 of the 3 equal parts. In the circle on the right, 2/3 of the circle is shaded (2 of the 3 equal parts).

Fraction

A fraction is written [latex]\frac{a}{b}[/latex] where [latex]b\ne 0[/latex] and

  • [latex]a[/latex] is the numerator and [latex]b[/latex] is the denominator

A fraction represents parts of a whole. The denominator [latex]b[/latex] is the number of equal parts the whole has been divided into, and the numerator [latex]a[/latex] indicates how many parts are included.

If a whole pie has been cut into 6 pieces and we eat all 6 pieces, we ate [latex]\frac66[/latex] pieces, or, in other words, one whole pie.

A circle is shown and is divided into six section. All sections are shaded.
Figure 1.4.2

So [latex]\frac{6}{6}=1[/latex]. This leads us to the property of one that tells us that any number, except zero, divided by itself is 1.

Property of One

[latex]\begin{array}{cccc}\frac{a}{a}=1\hfill & &\left(a\ne 0\right)\hfill \end{array}[/latex]. Any number, except zero, divided by itself is one.

If a pie was cut in 6 pieces and we ate all 6, we ate [latex]\frac{6}{6}[/latex] pieces, or, in other words, one whole pie. If the pie was cut into 8 pieces and we ate all 8, we ate [latex]\frac{8}{8}[/latex] pieces, or one whole pie. We ate the same amount—one whole pie.

The fractions [latex]\frac{6}{6}[/latex] and [latex]\frac{8}{8}[/latex] have the same value, 1, and so they are called equivalent fractions. Equivalent fractions are fractions that have the same value.

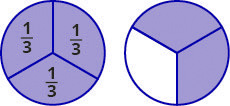
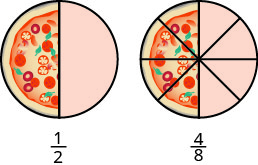
Let’s think of pizzas this time. Figure 1.4.2 shows two images: a single pizza on the left, cut into two equal pieces, and a second pizza of the same size, cut into eight pieces on the right. This is a way to show that [latex]\frac{1}{2}[/latex] is equivalent to [latex]\frac{4}{8}[/latex]. In other words, they are equivalent fractions.

Since the same amount is of each pizza is shaded, we see that [latex]\frac{1}{2}[/latex] is equivalent to [latex]\frac{4}{8}[/latex]. They are equivalent fractions.

A circle is shown that is divided into eight equal wedges by lines. The left side of the circle is a pizza with four sections making up the pizza slices. The right side has four shaded sections. Below the diagram is the fraction four eighths.
Figure 1.4.3. Since the same amount is of each pizza is shaded, we see that [latex]\frac{1}{2}[/latex] is equivalent to [latex]\frac{4}{8}[/latex]. They are equivalent fractions.

Equivalent Fractions

Equivalent fractions are fractions that have the same value.

How can we use mathematics to change [latex]\frac{1}{2}[/latex] into [latex]\frac{4}{8}[/latex]? How could we take a pizza that is cut into 2 pieces and cut it into 8 pieces? We could cut each of the 2 larger pieces into 4 smaller pieces! The whole pizza would then be cut into 8 pieces instead of just 2. Mathematically, what we’ve described could be written like this as [latex]\frac{1\times4}{2\times4}=\frac{4}{8}[/latex]. See Figure. 1.4.3.

Cutting each half of the pizza into [latex]4[/latex] pieces, gives us pizza cut into 8 pieces: [latex]\frac{1\times4}{2\times4}=\frac{4}{8}[/latex].

A circle is shown and is divided in half by a vertical black line. It is further divided into eighths by the addition of dotted red lines.
1.4.4. Cutting each half of the pizza into 4 pieces, gives us pizza cut into 8 pieces.

This model leads to the following property:

Equivalent Fractions Property

If [latex]a,b,c[/latex] are numbers where [latex]b\ne 0,c\ne 0[/latex], then

[latex]\frac{a}{b}=\frac{ac}{bc}[/latex] and [latex]\frac{ac}{bc}=\frac{a}{b}[/latex]

If we had cut the pizza differently, we could get

[latex]\frac{1\cdot2}{2\cdot2}=\frac24[/latex]   so   [latex]\frac12=\frac24[/latex]

[latex]\frac{1\cdot3}{2\cdot3}=\frac36[/latex]   so   [latex]\frac12=\frac36[/latex]

[latex]\frac{1\cdot10}{2\cdot10}=\frac{10}{20}[/latex]   so   [latex]\frac12=\frac{10}{20}[/latex]

So, we say [latex]\frac{1}{2},\frac{2}{4},\frac{3}{6},\text{and}\frac{10}{20}[/latex] are equivalent fractions.

Example 1.4.1

Find three fractions equivalent to [latex]\frac{2}{5}[/latex]

Solution

To find a fraction equivalent to [latex]\frac{2}{5}[/latex], we multiply the numerator and denominator by the same number. We can choose any number, except for zero. Let’s multiply them by 2, 3, and then 5.

[latex]\begin{eqnarray*}\frac{2\;\times\;2}{5\;\times\;2}=\frac4{10}\;\;\;\;\;\;\;\;\;\;\;\;\frac{2\;\times\;3}{5\;\times\;3}=\frac6{15}\;\;\;\;\;\;\;\;\;\;\;\;\frac{2\;\times\;5}{5\;\times\;5}=\frac{10}{25}\end{eqnarray*}[/latex]

So, [latex]\frac{4}{10},\frac{6}{15},\text{and}\frac{10}{25}[/latex] are equivalent to [latex]\frac{2}{5}[/latex].

Try It

1) Find three fractions equivalent to [latex]\frac{3}{5}[/latex]

Solution

[latex]\frac{6}{10},\frac{9}{15},\frac{12}{20}[/latex]; answers may vary

2) Find three fractions equivalent to [latex]\frac{4}{5}[/latex]

Solution

[latex]\frac{8}{10},\frac{12}{15},\frac{16}{20}[/latex]; answers may vary

Simplify Fractions

A fraction is considered simplified if there are no common factors, other than 1, in its numerator and denominator.

For example,

      • [latex]\frac{2}{3}[/latex] is simplified because there are no common factors of 2 and 3.
      • [latex]\frac{10}{15}[/latex] is not simplified because 5 is a common factor of 10 and 15.

Simplified Fraction

A fraction is considered simplified if there are no common factors in its numerator and denominator.

The phrase reduce a fraction means to simplify the fraction. We simplify, or reduce, a fraction by removing the common factors of the numerator and denominator. A fraction is not simplified until all common factors have been removed. If an expression has fractions, it is not completely simplified until the fractions are simplified.

In Example 1.4.2, we used the equivalent fractions property to find equivalent fractions. Now we’ll use the equivalent fractions property in reverse to simplify fractions. We can rewrite the property to show both forms together.

Equivalent Fractions Property

If [latex]a,b,c[/latex] are numbers where [latex]b\ne 0,c\ne 0[/latex], then [latex]\frac{a}{b}=\frac{ac}{bc}[/latex] and [latex]\frac{ac}{bc}=\frac{a}{b}[/latex]

Example 1.4.2

Simplify: [latex]-\frac{32}{56}[/latex].

Solution

Step 1: Rewrite the numerator and denominator showing the common factors.

[latex]-\frac{4\times8}{7\times8}[/latex]

Step 2: Simplify using the equivalent fractions property.

[latex]-\frac{4}{7}[/latex]

Notice that the fraction [latex]-\frac{4}{7}[/latex] is simplified because there are no more common factors.

Try It

3) Simplify: [latex]-\frac{42}{54}[/latex]

Solution

[latex]-\frac{7}{9}[/latex]

4) Simplify: [latex]-\frac{45}{81}[/latex]

Solution

[latex]-\frac{5}{9}[/latex]

Sometimes it may not be easy to find common factors of the numerator and denominator. When this happens, a good idea is to factor the numerator and the denominator into prime numbers. Then divide out the common factors using the equivalent fractions property.

Example 1.4.3

Simplify: [latex]-\frac{210}{385}[/latex]

Solution

Step 1: Rewrite the numerator and denominator to show the common factors. If needed, factor the numerator and denominator into prime numbers first.

Rewrite 210 and 385 as the product of the primes.

[latex]\begin{eqnarray*}&=&-\frac{210}{385}\\&=&-\frac{2\;\times\;3\;\times\;5\;\times\;7}{5\;\times\;7\;\times\;11}\end{eqnarray*}[/latex]

Step 2: Simplify using the equivalent fractions property by dividing out common factors.

Mark the common factors 5 and 7. Divide out the common factors.

[latex]\begin{eqnarray*}&=&\;-\frac{2\;\times\;3\;\times\cancel{\;8\;}\times\cancel{\;7}}{\cancel{8\;}\times\;\cancel{7\;}\times\;11}\\&=&-\frac{2\;\times\;3}{11}\end{eqnarray*}[/latex]

Step 3: Multiply the remaining factors, if necessary.

[latex]-\frac{6}{11}[/latex]

Try It

5) Simplify: [latex]-\frac{69}{120}[/latex]

Solution

[latex]-\frac{23}{40}[/latex]

6) Simplify: [latex]-\frac{120}{192}[/latex]

Solution

[latex]-\frac{5}{8}[/latex]

We now summarize the steps you should follow to simplify fractions.

HOW TO

Simplify a Fraction.

  1. Rewrite the numerator and denominator to show the common factors.
     If needed, factor the numerator and denominator into prime numbers first.
  2. Simplify using the equivalent fractions property by dividing out common factors.
  3. Multiply any remaining factors, if needed.

Example 1.4.4

Simplify: [latex]\frac{5x}{5y}[/latex].

Solution

Step 1: Rewrite showing the common factors, then divide out the common factors.

[latex]\frac{\cancel{5\;}\times\;x}{\cancel{5\;}\times\;y}[/latex]

Step 2: Simplify.

[latex]\frac{x}{y}[/latex]

Try It

7) Simplify: [latex]\frac{7x}{7y}[/latex]

Solution

[latex]\frac{x}{y}[/latex]

8)Simplify: [latex]\frac{3a}{3b}[/latex]

Solution

[latex]\frac{a}{b}[/latex]

Multiply Fractions

Many people find multiplying and dividing fractions easier than adding and subtracting fractions. So we will start with fraction multiplication.

We’ll use a model to show you how to multiply two fractions and to help you remember the procedure. Let’s start with [latex]\frac{3}{4}[/latex].

A rectangle made up of four squares in a row. The first three squares are shaded.
Figure 1.4.5

Now we’ll take [latex]\frac{1}{2}[/latex] of [latex]\frac{3}{4}[/latex].

A rectangle made up of four squares in a row. The first three squares are shaded. The bottom halves of the first three squares are shaded darker with diagonal lines.
Figure 1.4.6

Notice that now, the whole is divided into 8 equal parts. So [latex]\frac12\times\frac34=\frac38[/latex]

To multiply fractions, we multiply the numerators and multiply the denominators.

Fraction Multiplication

If [latex]a,b,c\;\text{and}\;d[/latex] are numbers where [latex]b\ne 0\;\text{and}\;d\ne 0[/latex], then [latex]\frac{a}{b}\times\frac{c}{d}=\frac{ac}{bd}[/latex].

To multiply fractions, multiply the numerators and multiply the denominators.

When multiplying fractions, the properties of positive and negative numbers still apply, of course. It is a good idea to determine the sign of the product as the first step. In Example 1.4.5, we will multiply negative and positive, so the product will be negative.

Example 1.4.5

Multiply: [latex]-\frac{11}{12}\times\frac{5}{7}[/latex]

Solution

The first step is to find the sign of the product. Since the signs are the different, the product is negative.

Step 1: Determine the sign of the product; multiply.

[latex]-\frac{11\;\times\;5}{12\;\times\;7}[/latex]

Step 2: Are there any common factors in the numerator and the denominator? No.

[latex]-\frac{55}{84}[/latex]

Try It

9) Multiply: [latex]-\frac{10}{28}\times\frac{8}{15}[/latex]

Solution

[latex]-\frac{4}{21}[/latex]

10) Multiply: [latex]-\frac{9}{20}\times\frac{5}{12}[/latex]

Solution

[latex]-\frac{3}{16}[/latex]

When multiplying a fraction by an integer, it may be helpful to write the integer as a fraction. Any integer, [latex]a[/latex], can be written as [latex]\frac{a}{1}[/latex]. So, for example, [latex]3=\frac{3}{1}[/latex].

Example 1.4.6

Multiply: [latex]-\frac{12}{5}\left(-20x\right)[/latex]

Solution

Determine the sign of the product. The signs are the same, so the product is positive.

Step 1: Write [latex]20x[/latex] as a fraction.

[latex]\frac{12}{5}\left(\frac{20x}{1}\right)[/latex]

Step 2: Multiply.
Step 3: Rewrite 20 to show the common factor 5 and divide it out.

[latex]\frac{12\;\times\;4\;\times\;\cancel5x}{\cancel5\;\times\;1}[/latex]

Step 4: Simplify.

[latex]48x[/latex]

Try It

11) Multiply: [latex]\frac{11}{3}\left(-9a\right)[/latex]

Solution

[latex]-33a[/latex]

12) Multiply: [latex]\frac{13}{7}\left(-14b\right)[/latex]

Solution

[latex]-2b[/latex]

Divide Fractions

Now that we know how to multiply fractions, we are almost ready to divide. Before we can do that, that we need some vocabulary.

The reciprocal of a fraction is found by inverting the fraction, placing the numerator in the denominator and the denominator in the numerator. The reciprocal of [latex]\frac{2}{3}[/latex] is [latex]\frac{3}{20}[/latex].

Notice that [latex]\frac{2}{3}\cdot\frac{3}{2}=1[/latex]. A number and its reciprocal multiply to 1.

To get a product of positive 1 when multiplying two numbers, the numbers must have the same sign. So reciprocals must have the same sign.

The reciprocal of [latex]-\frac{10}{7}[/latex] is [latex]-\frac{7}{10}[/latex], since [latex]-\frac{10}{7}\left(-\frac{7}{10}\right)=1[/latex].

Reciprocal

The reciprocal of [latex]\frac{a}{b}[/latex] is [latex]\frac{b}{a}[/latex].

A number and its reciprocal multiply to one [latex]\frac ab\times\frac ba=1[/latex]

To divide fractions, we multiply the first fraction by the reciprocal of the second.

Fraction Division

If [latex]a,b,c\;\text{and}\;d[/latex] are numbers where [latex]b\ne 0,c\ne 0\;\text{and}\;d\ne 0[/latex], then

[latex]\frac{a}{b}\div \frac{c}{d}=\frac{a}{b}\times\frac{d}{c}[/latex]

 

To divide fractions, we multiply the first fraction by the reciprocal of the second.

We need to say [latex]b\ne 0,c\ne 0\;\text{and}\;d\ne 0[/latex] to be sure we don’t divide by zero!

Example 1.4.7

Divide: [latex]-\frac{2}{3} \div \frac{n}{5}[/latex].

Solution

Step 1: To divide, multiply the first fraction by the reciprocal of the second.

[latex]-\frac{2}{3}\times\frac{5}{n}[/latex]

Step 2: Multiply.

[latex]-\frac{10}{3n}[/latex]

Try It

13) Divide: [latex]-\frac{3}{5}\div \frac{p}{7}[/latex]

Solution

[latex]-\frac{21}{5p}[/latex]

14) Divide: [latex]-\frac{5}{8}\div \frac{q}{3}[/latex]

Solution

[latex]-\frac{15}{8q}[/latex]

Example 1.4.8

Find the quotient: [latex]-\frac{7}{8}\div \left(-\frac{14}{27}\right)[/latex].

Solution

Step 1: To divide, multiply the first fraction by the reciprocal of the second.

[latex]-\frac{7}{18}\times\ -\frac{27}{14}[/latex]

Step 2: Determine the sign of the product, and then multiply.

[latex]\frac{7\times\ 27}{18\times\ 14}[/latex]

Step 3: Rewrite showing common factors.

[latex]\frac{\cancel{7\;}\times\cancel{\;9\;}\times\;3}{\cancel{9\;}\times\;2\;\times\cancel{\;7\;}\times\;2}[/latex]

Step 4: Remove common factors.

[latex]\frac3{2\;\times\;2}[/latex]

Step 5: Simplify.

[latex]\frac{3}{4}[/latex]

Try It

15) Find the quotient: [latex]-\frac{7}{27}\div \left(-\frac{35}{36}\right)[/latex]

Solution

[latex]\frac{4}{15}[/latex]

16) Find the quotient: [latex]-\frac{5}{14}\div \left(-\frac{15}{28}\right)[/latex]

Solution

[latex]\frac{2}{3}[/latex]

There are several ways to remember which steps to take to multiply or divide fractions. One way is to repeat the call outs to yourself. If you do this each time you do an exercise, you will have the steps memorized.

  • “To multiply fractions, multiply the numerators and multiply the denominators.”
  • “To divide fractions, multiply the first fraction by the reciprocal of the second.”

Another way is to keep two examples in mind:

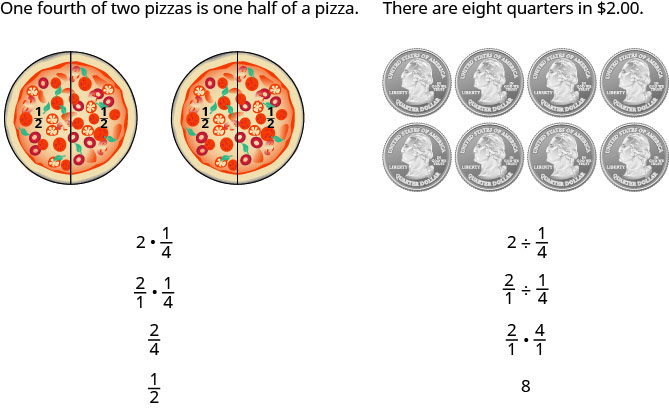
This is an image with two columns. The first column reads “One fourth of two pizzas is one half of a pizza. Below this are two pizzas side-by-side with a line down the center of each one representing one half. The halves are labeled “one half”. Under this is the equation “2 times 1 fourth”. Under this is another equation “two over 1 times 1 fourth.” Under this is the fraction two fourths and under this is the fraction one half. The next column reads “there are eight quarters in two dollars.” Under this are eight quarters in two rows of four. Under this is the fraction equation 2 divided by one fourth. Under this is the equation “two over one divided by one fourth.” Under this is two over one times four over one. Under this is the answer “8”.
Figure 1.4.7

The numerators or denominators of some fractions contain fractions themselves. A fraction in which the numerator or the denominator is a fraction is called a complex fraction.

Complex Fraction

A complex fraction is a fraction in which the numerator or the denominator contains a fraction.

Some examples of complex fractions are:

[latex]\frac{\frac{6}{7}}{3}\phantom{\rule{1em}{0ex}}\frac{\frac{3}{4}}{\frac{5}{8}}\phantom{\rule{1em}{0ex}}\frac{\frac{x}{2}}{\frac{5}{6}}[/latex]

To simplify a complex fraction, we remember that the fraction bar means division. For example, the complex fraction [latex]\frac{\frac{3}{4}}{\frac{5}{8}}[/latex] means [latex]\frac{3}{4}\div \frac{5}{8}[/latex].

Example 1.4.9

Simplify: [latex]\frac{\frac{3}{4}}{\frac{5}{8}}[/latex]

Solution

Step 1: Rewrite as division.

[latex]\frac34\div\frac58[/latex]

Step 2: Multiply the first fraction by the reciprocal of the second.

[latex]\frac{3}{4}\times \frac{8}{5}[/latex]

Step 3: Multiply.

[latex]\frac{3\;\times\;8}{4\;\times\;5}[/latex]

Step 4: Look for common factors.

[latex]\frac{3\;\times\;\cancel4\;\times\;2}{\cancel{4\;}\times\;5}[/latex]

Step 5: Divide out common factors and simplify.

[latex]\frac{6}{5}[/latex]

Try It

17) Simplify: [latex]\frac{\frac{2}{3}}{\frac{5}{6}}[/latex]

Solution

[latex]\frac{4}{5}[/latex]

18) Simplify: [latex]\frac{\frac{3}{7}}{\frac{6}{11}}[/latex]

Solution

[latex]\frac{11}{14}[/latex]

Example 1.4.10

Simplify: [latex]\frac{\frac{x}{2}}{\frac{xy}{6}}[/latex]

Solution

Step 1: Rewrite as division.

[latex]\frac x2\div\frac{xy}6[/latex]

Step 2: Multiply the first fraction by the reciprocal of the second.

[latex]\frac{x}{2}\times \frac{6}{xy}[/latex]

Step 3: Multiply.

[latex]\frac{x\;\times\;6}{2\;\times\;xy}[/latex]

Step 4: Look for common factors.

[latex]\frac{\cancel{x\;}\times\;3\;\times\;\cancel2}{\cancel{2\;}\times\cancel{\;x\;}\times\;y}[/latex]

Step 5: Divide out common factors and simplify.

[latex]\frac{3}{y}[/latex]

Try It

19) Simplify: [latex]\frac{\frac{a}{8}}{\frac{ab}{6}}[/latex]

Solution

[latex]\frac{3}{4b}[/latex]

20) Simplify: [latex]\frac{\frac{p}{2}}{\frac{pq}{8}}[/latex]

Solution

[latex]\frac{4}{2q}[/latex]

Simplify Expressions with a Fraction Bar

The line that separates the numerator from the denominator in a fraction is called a fraction bar. A fraction bar acts as grouping symbol. The order of operations then tells us to simplify the numerator and then the denominator. Then we divide.

To simplify the expression [latex]\frac{5-3}{7+1}[/latex], we first simplify the numerator and the denominator separately. Then we divide.

[latex]\begin{eqnarray*}&=&\frac{5-3}{7+1}\\&=&\frac28\\&=&\frac14\end{eqnarray*}[/latex]

HOW TO

Simplify an Expression with a Fraction Bar.

  1. Simplify the expression in the numerator.
  2. Simplify the expression in the denominator.
  3. Simplify the fraction.

Example 1.4.11

Simplify: [latex]\frac{4-2\left(3\right)}{{2}^{2}+2}[/latex]

Solution

Step 1: Use the order of operations to simplify the numerator and the denominator.

[latex]\frac{4-6}{4+2}[/latex]

Step 2: Simplify the numerator and the denominator.

[latex]\frac{-2}{6}[/latex]

Step 3: Simplify. A negative divided by a positive is negative.

[latex]-\frac{1}{3}[/latex]

Try It

21) Simplify: [latex]\frac{6-3\left(5\right)}{{3}^{2}+3}[/latex]

Solution

[latex]-\frac{3}{4}[/latex]

22) Simplify: [latex]\frac{4-4\left(6\right)}{{3}^{2}+3}[/latex]

Solution

[latex]-\frac{2}{3}[/latex]

Where does the negative sign go in a fraction? Usually the negative sign is in front of the fraction, but you will sometimes see a fraction with a negative numerator, or sometimes with a negative denominator. Remember that fractions represent division. When the numerator and denominator have different signs, the quotient is negative.

[latex]\begin{array}{cccccc}\frac{-1}{3}=-\frac{1}{3}\hfill & & & & & \frac{\text{negative}}{\text{positive}}=\text{negative}\hfill \\ \frac{1}{-3}=-\frac{1}{3}\hfill & & & & & \frac{\text{positive}}{\text{negative}}=\text{negative}\hfill \end{array}[/latex]

Placement of Negative Sign in a Fraction

For any positive numbers [latex]a[/latex] and [latex]b[/latex],

[latex]\frac{\text{−}a}{b}=\frac{a}{\text{−}b}=-\frac{a}{b}[/latex]

Example 1.4.12

Simplify: [latex]\frac{4\left(-3\right)+6\left(-2\right)}{-3\left(2\right)-2}[/latex]

Solution

Step 1: Multiply.

[latex]\frac{-12+\left(-12\right)}{-6-2}[/latex]

Step 2: Simplify.

[latex]\frac{-24}{-8}[/latex]

Step 3: Divide.

[latex]3[/latex]

Try It

23) Simplify: [latex]\frac{8\left(-2\right)+4\left(-3\right)}{-5\left(2\right)+3}[/latex]

Solution

4

24) Simplify: [latex]\frac{7\left(-1\right)+9\left(-3\right)}{-5\left(3\right)-2}[/latex]

Solution

2

Translate Phrases to Expressions with Fractions

Now that we have done some work with fractions, we are ready to translate phrases that would result in expressions with fractions.

The English words quotient and ratio are often used to describe fractions. Remember that “quotient” means division. The quotient of [latex]a[/latex] and [latex]b[/latex] is the result we get from dividing [latex]a[/latex] by [latex]b[/latex], or [latex]\frac{a}{b}[/latex].

Example 1.4.13

Translate the English phrase into an algebraic expression: the quotient of the difference of [latex]m[/latex] and [latex]n[/latex], and [latex]p[/latex].

Solution

We are looking for the quotient of  the difference of [latex]m[/latex] and [latex]n[/latex], and [latex]p[/latex]. This means we want to divide the difference of [latex]m[/latex] and [latex]n[/latex] by [latex]p[/latex].

[latex]\frac{m-n}{p}[/latex]

Try It

25) Translate the English phrase into an algebraic expression: the quotient of the difference of [latex]a[/latex] and [latex]b[/latex], and [latex]cd[/latex].

Solution

[latex]\frac{a-b}{cd}[/latex]

26) Translate the English phrase into an algebraic expression: the quotient of the sum of [latex]p[/latex] and [latex]q[/latex], and [latex]r[/latex]

Solution

[latex]\frac{p+q}{r}[/latex]

Add or Subtract Fractions with a Common Denominator

When we multiplied fractions, we just multiplied the numerators and multiplied the denominators right straight across. To add or subtract fractions, they must have a common denominator.

Fraction Addition and Subtraction

If [latex]a,b,\;\text{and}\;c[/latex] are numbers where [latex]c\ne 0[/latex], then

[latex]\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\phantom{\rule{1em}{0ex}}\text{and}\phantom{\rule{1em}{0ex}}\frac{a}{c}-\frac{b}{c}=\frac{a-b}{c}[/latex]

To add or subtract fractions, add or subtract the numerators and place the result over the common denominator.

Example 1.4.14

Find the sum: [latex]\frac{x}{3}+\frac{2}{3}[/latex].

Solution

Step 1: Add the numerators and place the sum over the common denominator.

[latex]\frac{x+2}{3}[/latex]

Try It

27) Find the sum: [latex]\frac{x}{4}+\frac{3}{4}[/latex]

Solution

[latex]\frac{x+3}{4}[/latex]

28) Find the sum: [latex]\frac{y}{8}+\frac{5}{8}[/latex]

Solution

[latex]\frac{y+5}{8}[/latex]

Example 1.4.15

Find the difference: [latex]-\frac{23}{24}-\frac{13}{24}[/latex].

Solution

Step 1: Subtract the numerators and place the difference over the common denominator.

[latex]\frac{-23-13}{24}[/latex]

Step 2: Simplify.

[latex]\frac{-36}{24}[/latex]

Step 3: Simplify. Remember, [latex]-\frac{a}{b}=\frac{\text{−}a}{b}[/latex].

[latex]-\frac{3}{2}[/latex]

Try It

29) Find the difference: [latex]-\frac{19}{28}-\frac{7}{28}[/latex]

Solution

[latex]-\frac{26}{28}[/latex]

30) Find the difference: [latex]-\frac{27}{32}-\frac{1}{32}[/latex]

Solution

[latex]-\frac{7}{8}[/latex]

Example 1.4.16

Simplify: [latex]-\frac{10}{x}-\frac{4}{x}[/latex]

Solution

Step 1: Subtract the numerators and place the difference over the common denominator.

[latex]\frac{-14}{x}[/latex]

Step 2: Rewrite with the sign in front of the fraction.

[latex]-\frac{14}{x}[/latex]

Try It

31) Find the difference: [latex]-\frac{9}{x}-\frac{7}{x}[/latex]

Solution

[latex]-\frac{16}{x}[/latex]

32) Find the difference: [latex]-\frac{17}{a}-\frac{5}{a}[/latex]

Solution

[latex]-\frac{22}{a}[/latex]

Now we will do an example that has both addition and subtraction.

Example 1.4.17

Simplify: [latex]\frac{3}{8}+\left(-\frac{5}{8}\right)-\frac{1}{8}[/latex]

Solution

Step 1: Add and subtract fractions—do they have a common denominator? Yes.

[latex]\frac{3}{8}+\left(-\frac{5}{8}\right)-\frac{1}{8}[/latex].

Step 2: Add and subtract the numerators and place the difference over the common denominator.

[latex]\frac{3+\left(-5\right)-1}{8}[/latex]

Step 3: Simplify left to right.

[latex]\frac{-2-1}{8}[/latex]

Step 4: Simplify.

[latex]-\frac{3}{8}[/latex]

Try It

33) Simplify: [latex]\frac{-2}{9}+\left(-\frac{4}{9}\right)-\frac{7}{9}[/latex]

Solution

[latex]-1[/latex]

34) Simplify: [latex]\frac{5}{9}+\left(-\frac{4}{9}\right)-\frac{7}{9}[/latex]

Solution

[latex]-\frac{2}{3}[/latex]

Add or Subtract Fractions with Different Denominators

As we have seen, to add or subtract fractions, their denominators must be the same. The least common denominator (LCD) of two fractions is the smallest number that can be used as a common denominator of the fractions. The LCD of the two fractions is the least common multiple (LCM) of their denominators.

Least Common Denominator

The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.

After we find the least common denominator of two fractions, we convert the fractions to equivalent fractions with the LCD. Putting these steps together allows us to add and subtract fractions because their denominators will be the same!

Example 1.4.18

Add: [latex]\frac{7}{12}+\frac{5}{18}[/latex]

Solution

Step 1: Do they have a common denominator?

[latex]\begin{eqnarray*}\left.\begin{array}{r}12\;=\;2\;\times\;2\;\times\;3\\18\;=\;2\;\times\;3\;\times\;3\end{array}\right\}\;\text{LCD}=2\;\times\;2\;\times\;3\;\times\;3\;=\;36\end{eqnarray*}[/latex]

No – rewrite each fraction with the LCD (least common denominator).

[latex]\begin{eqnarray*}&=&\frac7{12}+\frac5{18}\\&=&\frac{7\;\times\;3}{12\;\times\;3}+\frac{5\;\times\;2}{18\;\times\;2}\\&=&\;\frac{21}{36}+\frac{10}{36}\;\text{Do not simplify LCD fractions.}\\\end{eqnarray*}[/latex]

 

Step 2: Add or subtract the fractions.

Add.

[latex]\frac{31}{36}[/latex]

Step 3: Simplify, if possible.

Because 31 is a prime number, it has no factors in common with 36. The answer is simplified.

Try It

35) Add: [latex]\frac{7}{12}+\frac{11}{15}[/latex]

Solution

[latex]\frac{79}{60}[/latex]

36) Add: [latex]\frac{13}{15}+\frac{17}{20}[/latex]

Solution

[latex]\frac{103}{60}[/latex]

HOW TO

Add or Subtract Fractions.

  1. Do they have a common denominator?
    • Yes—go to step 2.
    • No—rewrite each fraction with the LCD (least common denominator). Find the LCD. Change each fraction into an equivalent fraction with the LCD as its denominator.
  2. Add or subtract the fractions.
  3. Simplify, if possible.

When finding the equivalent fractions needed to create the common denominators, there is a quick way to find the number we need to multiply both the numerator and denominator. This method works if we found the LCD by factoring into primes.

Look at the factors of the LCD and then at each column above those factors. The “missing” factors of each denominator are the numbers we need.

The number 12 is factored into 2 times 2 times 3 with an extra space after the 3, and the number 18 is factored into 2 times 3 times 3 with an extra space between the 2 and the first 3. There are arrows pointing to these extra spaces that are marked “missing factors.” The LCD is marked as 2 times 2 times 3 times 3, which is equal to 36. The numbers that create the LCD are the factors from 12 and 18, with the common factors counted only once (namely, the first 2 and the first 3).
Figure 1.4.8

In the above figure the LCD, 36, has two factors of 2 and two factors of 3.

The numerator 12 has two factors of 2 but only one of 3—so it is “missing” one 3—we multiply the numerator and denominator by 3.

The numerator 18 is missing one factor of 2—so we multiply the numerator and denominator by 2.

We will apply this method as we subtract the fractions in Example 1.4.19

Example 1.4.19

Subtract: [latex]\frac{7}{15}-\frac{19}{24}[/latex]

Solution

Step 1: Find the LCD.

Do the fractions have a common denominator? No, so we need to find the LCD.

Notice, 15 is “missing” three factors of 2 and 24 is “missing” the 5 from the factors of the LCD. So we multiply 8 in the first fraction and 5 in the second fraction to get the LCD.

[latex]\begin{eqnarray*}\left.\begin{array}{r}15\;&=&\;3\;\times\;5\\24\;&=&\;2\;\times\;2\;\times\;2\;\times\;3\end{array}\right\}\;LCD=\;2\;\times\;2\;\times\;2\;\times\;3\;\times\;5\;=\;120\end{eqnarray*}[/latex]
[latex]\begin{eqnarray*}&=&\frac7{15}-\frac{19}{24}\\&=&\;\frac{7\;\times\;8}{15\;\times\;8}-\frac{19\;\times\;5}{24\;\times\;5}\end{eqnarray*}[/latex]

Step 2: Rewrite as equivalent fractions with the LCD.

[latex]\frac{56}{120}-\frac{95}{120}[/latex]

Step 3: Subtract.

[latex]\frac{39}{120}[/latex]

Step 4: Check to see if the answer can be simplified.

[latex]\frac{13\;\times\;3}{40\;\times\;3}[/latex]

Step 5: Simplify.

Both 39 and 120 have a factor of 3.

[latex]\frac{13}{40}[/latex]

Do not simplify the equivalent fractions! If you do, you’ll get back to the original fractions and lose the common denominator!

Try It

37) Subtract: [latex]\frac{13}{24}-\frac{17}{32}[/latex]

Solution

[latex]\frac{1}{96}[/latex]

38) Subtract: [latex]\frac{21}{32}-\frac{9}{28}[/latex]

Solution

[latex]\frac{75}{224}[/latex]

In the next example, one of the fractions has a variable in its numerator. Notice that we do the same steps as when both numerators are numbers.

Example 1.4.20

Add: [latex]\frac{3}{5}+\frac{x}{8}[/latex]

Solution

The fractions have different denominators.

Step 1: Find the LCD.

[latex]\left.\begin{array}{r}5\;&=&\;5\\8\;&=&\;2\;\times\;2\;\times\;2\end{array}\right\}LCD=\;2\;\times\;2\;\times\;2\;\times\;5\;=\;40[/latex]

Step 2: Rewrite as equivalent fractions with the LCD.

[latex]\frac{3\;\times\;8}{5\;\times\;8}+\frac{x\;\times\;5}{8\;\times\;5}[/latex]

Step 3: Simplify.

[latex]\frac{24}{40}+\frac{5x}{40}[/latex]

Step 4: Add.

[latex]\frac{24+5x}{40}[/latex]

Remember, we can only add like terms: [latex]24[/latex] and [latex]5x[/latex] are not like terms.

Try It

39) Add: [latex]\frac{y}{6}+\frac{7}{9}[/latex]

Solution

[latex]\frac{9y+42}{54}[/latex]

40) Add: [latex]\frac{x}{6}+\frac{7}{15}[/latex]

Solution

[latex]\frac{15x+42}{135}[/latex]

We now have all four operations for fractions. The table below summarizes fraction operations.

Fraction Multiplication Fraction Division
[latex]\frac{a}{b}\times\frac{c}{d}=\frac{ac}{bd}[/latex]

Multiply the numerators and multiply the denominators		 [latex]\frac{a}{b}\div \frac{c}{d}=\frac{a}{b}\times\frac{d}{c}[/latex]

Multiply the first fraction by the reciprocal of the second.
Fraction Addition Fraction Subtraction
[latex]\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}[/latex]

Add the numerators and place the sum over the common denominator.		 [latex]\frac{a}{c}-\frac{b}{c}=\frac{a-b}{c}[/latex]

Subtract the numerators and place the difference over the common denominator.
To multiply or divide fractions, an LCD is NOT needed.
 To add or subtract fractions, an LCD is needed.

Example 1.4.21

Simplify:

  1. [latex]\frac{5x}{6}-\frac{3}{10}[/latex]
  2. [latex]\frac{5x}{6}\times\frac{3}{10}[/latex]
Solution

First ask, “What is the operation?” Once we identify the operation that will determine whether we need a common denominator. Remember, we need a common denominator to add or subtract, but not to multiply or divide.

a. What is the operation? The operation is subtraction.

Step 1: Do the fractions have a common denominator? No.

[latex]\frac{5x}{6}-\frac{3}{10}[/latex]

Step 2: Rewrite each fraction as an equivalent fraction with the LCD.

[latex]\frac{5x\times5}{6\times5}-\frac{3\times3}{10\times3}[/latex]

Step 3: Subtract the numerators and place the difference over the common denominators.

[latex]\frac{25x}{30}-\frac{9}{30}[/latex]

Step 4: Simplify, if possible There are no common factors. The fraction is simplified.

[latex]\frac{25x-9}{30}[/latex]

b. What is the operation? Multiplication.

Step 1: To multiply fractions, multiply the numerators and multiply the denominators.

[latex]\frac{5x\times3}{6\times10}[/latex]

Step 2: Rewrite, showing common factors.

[latex]\frac{\cancel5x\;\times\;\cancel3}{2\;\times\;\cancel3\;\times\;2\;\times\;\cancel5}[/latex]

Step 3: Remove common factors.
Step 4: Simplify.

[latex]\frac{x}{4}[/latex]

Notice we needed an LCD to add [latex]\frac{5x}{6}-\frac{3}{10}[/latex], but not to multiply [latex]\frac{5x}{6}\times\frac{3}{10}[/latex].

Try It

41) Simplify:

a. [latex]\frac{3a}{4}-\frac{8}{9}[/latex]

b. [latex]\frac{3a}{4}\times\frac{8}{9}[/latex]

Solution

a. [latex]\frac{27a-32}{36}[/latex]

b. [latex]\frac{2a}{3}[/latex]

42) Simplify:

a. [latex]\frac{4k}{5}-\frac{1}{6}[/latex]

b. [latex]\frac{4k}{5}\times\frac{1}{6}[/latex]

Solution

a. [latex]\frac{24k-5}{30}[/latex]

b. [latex]\frac{2k}{15}[/latex]

Use the Order of Operations to Simplify Complex Fractions

We have seen that a complex fraction is a fraction in which the numerator or denominator contains a fraction. The fraction bar indicates division. We simplified the complex fraction [latex]\frac{\frac{3}{4}}{\frac{5}{8}}[/latex] by dividing [latex]\frac{3}{4}[/latex] by [latex]\frac{5}{8}[/latex].

Now we’ll look at complex fractions where the numerator or denominator contains an expression that can be simplified. So we first must completely simplify the numerator and denominator separately using the order of operations. Then we divide the numerator by the denominator.

Example 1.4.22

Simplify: [latex]\frac{{\left(\frac{1}{2}\right)}^{2}}{4+{3}^{2}}[/latex].

Solution

Step 1: Simplify the numerator.

*Remember, [latex]\left(\frac12\right)^2[/latex] means [latex]\frac12\cdot\frac12[/latex]

[latex]\begin{eqnarray*}&=&\frac{\left({\displaystyle\frac12}\right)^2}{4+3^2}\\&=&\;\frac{\displaystyle\frac14}{4+3^2}\end{eqnarray*}[/latex]

Step 2: Simplify the denominator.

[latex]\begin{eqnarray*}&=&\frac{\displaystyle\frac14}{4+9}\\&=&\;\frac{\displaystyle\frac14}{13}\end{eqnarray*}[/latex]

Step 3: Divide the numerator by the denominator. Simplify if possible.

*Remember, [latex]13=\frac{13}{1}[/latex]

[latex]\begin{eqnarray*}&=&\frac14\div13\\&=&\;\frac14\times\frac1{13}\\&=&\frac1{52}\end{eqnarray*}[/latex]

Try It

43) Simplify: [latex]\frac{{\left(\frac{1}{3}\right)}^{2}}{{2}^{3}+2}[/latex]

Solution

[latex]\frac{1}{90}[/latex]

44) Simplify: [latex]\frac{1+{4}^{2}}{{\left(\frac{1}{4}\right)}^{2}}[/latex]

Solution

[latex]272[/latex]

Simplify Complex Fractions

  1. Simplify the numerator.
  2. Simplify the denominator.
  3. Divide the numerator by the denominator. Simplify if possible.

Example 1.4.23

Simplify: [latex]\frac{\frac{1}{2}+\frac{2}{3}}{\frac{3}{4}-\frac{1}{6}}[/latex]

Solution

It may help to put parentheses around the numerator and the denominator.

Step 1: Simplify the numerator (LCD = 6) and simplify the denominator (LCD = 12).

[latex]\frac{\left(\frac{3}{6}+\frac{4}{6}\right)}{\left(\frac{9}{12}-\frac{2}{12}\right)}[/latex]

Step 2: Simplify.

[latex]\frac{\left(\frac{7}{6}\right)}{\left(\frac{7}{12}\right)}[/latex]

Step 3: Divide the numerator by the denominator.

[latex]\frac{7}{6}\times\frac{12}{7}[/latex]

Step 4: Simplify.
Step 5: Divide out common factors.

[latex]\frac{7\times6\times2}{6\times7}[/latex]

Step 6: Simplify.

[latex]2[/latex]

Try It

45) Simplify: [latex]\frac{\frac{1}{3}+\frac{1}{2}}{\frac{3}{4}-\frac{1}{3}}[/latex]

Solution

2

46) Simplify: [latex]\frac{\frac{2}{3}-\frac{1}{2}}{\frac{1}{4}+\frac{1}{3}}[/latex]

Solution

[latex]\frac{2}{7}[/latex]

Evaluate Variable Expressions with Fractions

We have evaluated expressions before, but now we can evaluate expressions with fractions. Remember, to evaluate an expression, we substitute the value of the variable into the expression and then simplify.

Example 1.4.24

Evaluate [latex]x+\frac{1}{3}[/latex] when

a. [latex]x=-\frac{1}{3}[/latex]

b. [latex]x=-\frac{3}{4}[/latex]

Solution

a. To evaluate [latex]x+\frac{1}{3}[/latex] when [latex]x=-\frac{1}{3}[/latex], substitute [latex]-\frac{1}{3}[/latex] for [latex]x[/latex] in the expression.

Step 1: Substitute [latex]-\frac13[/latex] for [latex]x[/latex].

[latex]-\frac13+\frac13[/latex]

Step 2: Simplify.

[latex]0[/latex]

b. To evaluate [latex]x+\frac{1}{3}[/latex] when [latex]x=-\frac{3}{4}[/latex], we substitute [latex]-\frac{3}{4}[/latex] for [latex]x[/latex] in the expression.

Step 1: Substitute [latex]-\frac34[/latex] for [latex]x[/latex].

[latex]-\frac34+\frac13[/latex]

Step 2: Rewrite as equivalent fractions with the LCD, [latex]12[/latex].

[latex]-\frac{3\;\times\;3}{4\;\times\;3}+\frac{1\;\times\;4}{3\;\times\;4}[/latex]

Step 3:Simplify.

[latex]-\frac9{12}+\frac4{12}[/latex]

Step 4:Add.

[latex]-\frac{5}{12}[/latex]

Try It

47) Evaluate [latex]x+\frac{3}{4}[/latex] when

a. [latex]x=-\frac{7}{4}[/latex]

b. [latex]x=-\frac{5}{4}[/latex]

Solution

a. [latex]-1[/latex]

b. [latex]\frac{1}{2}[/latex]

48) Evaluate [latex]y+\frac{1}{2}[/latex] when

a. [latex]y=\frac{2}{3}[/latex]

b. [latex]y=-\frac{3}{4}[/latex]

Solution

a. [latex]\frac{7}{6}[/latex]

b. [latex]-\frac{1}{12}[/latex]

Example 1.4.25

Evaluate [latex]-\frac{5}{6}-y[/latex] when [latex]y=-\frac{2}{3}[/latex]

Solution

Step 1:  Substitute [latex]-\frac23[/latex] for [latex]y[/latex].

[latex]-\frac56-\left(-\frac23\right)[/latex]

Step 2: Rewrite as equivalent fractions with the LCD, [latex]6[/latex].

[latex]-\frac56-\left(-\frac46\right)[/latex]

Step 3: Subtract.

[latex]-\frac{5-\left(-4\right)}6[/latex]

Step 4: Simplify.

[latex]-\frac{1}{6}[/latex]

Try It

49) Evaluate [latex]-\frac{1}{2}-y[/latex] when [latex]y=-\frac{1}{4}[/latex]

Solution

[latex]-\frac{1}{4}[/latex]

50) Evaluate [latex]-\frac{3}{8}-y[/latex] when [latex]x=-\frac{5}{2}[/latex]

Solution

[latex]-\frac{17}{8}[/latex]

Example 1.4.26

Evaluate [latex]2{x}^{2}y[/latex] when [latex]x=\frac{1}{4}[/latex] and [latex]y=-\frac{2}{3}[/latex]

Solution

Substitute the values into the expression.

Step 1: Substitute[latex]\frac14[/latex] for [latex]x[/latex] and [latex]-\frac23[/latex] for [latex]y[/latex].

[latex]2\left(\frac14\right)^2\left(-\frac23\right)[/latex]

Step 2: Simplify exponents first.

[latex]2\left(\frac{1}{16}\right)\left(-\frac{2}{3}\right)[/latex]

Step 3: Multiply. Divide out the common factors. Notice we write [latex]16[/latex] as [latex]2\cdot 2\cdot 4[/latex] to make it easy to remove common factors.

[latex]\frac{\cancel2\;\times\;1\;\times\;\cancel2}{\cancel2\;\times\;\cancel2\;\times\;4\;\times\;3}[/latex]

Step 4: Simplify.

[latex]\frac{1}{12}[/latex]

 

Try It

51) Evaluate [latex]3a{b}^{2}[/latex] when [latex]a=-\frac{2}{3}[/latex] and [latex]b=-\frac{1}{2}[/latex]

Solution

[latex]-\frac{1}{2}[/latex]

52) Evaluate [latex]4{c}^{3}d[/latex] when [latex]c=-\frac{1}{2}[/latex] and [latex]d=-\frac{4}{3}[/latex]

Solution

[latex]\frac{2}{3}[/latex]

The next example will have only variables, no constants.

Example 1.4.27

Evaluate [latex]\frac{p+q}{r}[/latex] when [latex]p=-4,q=-2,\text{and}r=8[/latex]

Solution

To evaluate [latex]\frac{p+q}{r}[/latex] when [latex]p=-4,q=-2,\text{and}r=8[/latex], we substitute the values into the expression.

Step 1: Substitute [latex]−4[/latex] for [latex]p[/latex], [latex]−2[/latex] for [latex]q[/latex], and [latex]8[/latex] for [latex]r[/latex].

[latex]\frac{-4+\left(-2\right)}8[/latex]

Step 2: Add in the numerator first.

[latex]\frac{-6}{8}[/latex]

Step 3: Simplify.

[latex]-\frac{3}{4}[/latex]

Try It

53) Evaluate [latex]\frac{a+b}{c}[/latex] when [latex]a=-8,b=-7,\text{and}c=6[/latex]

Solution

[latex]-\frac{5}{2}[/latex]

54) Evaluate [latex]\frac{x+y}{z}[/latex] when [latex]x=9,y=-18,\text{and}z=-6[/latex]

Solution

[latex]\frac{3}{2}[/latex]

Key Concepts

  • Equivalent Fractions Property: If [latex]a,b,c[/latex] are numbers where [latex]b\ne 0,c\ne 0[/latex], then
     [latex]\frac{a}{b}=\frac{a\times c}{b \times c}[/latex] and [latex]\frac{a \times c}{b \times c}=\frac{a}{b}[/latex].
  • Fraction Division: If [latex]a,b,c\;\text{and}\;d[/latex] are numbers where [latex]b\ne 0,c\ne 0,\;\text{and}\;d\ne 0[/latex], then [latex]\frac{a}{b}\div\frac{c}{d}=\frac{a}{b}\times\frac{d}{c}[/latex]. To divide fractions, multiply the first fraction by the reciprocal of the second.
  • Fraction Multiplication: If [latex]a,b,c\;\text{and}\;d[/latex] are numbers where [latex]b\ne 0,\;\text{and}\;d\ne 0[/latex], then [latex]\frac{a}{b}\times\frac{c}{d}=\frac{ac}{bd}[/latex]. To multiply fractions, multiply the numerators and multiply the denominators.
  • Placement of Negative Sign in a Fraction: For any positive numbers [latex]a\text{ and }b[/latex], [latex]\frac{-a}{b}=\frac{a}{-b}=-\frac{a}{b}[/latex].
  • Property of One: [latex]\frac{a}{a}=1[/latex]; Any number, except zero, divided by itself is one.
  • Simplify a Fraction
    1. Rewrite the numerator and denominator to show the common factors. If needed, factor the numerator and denominator into prime numbers first.
    2. Simplify using the equivalent fractions property by dividing out common factors.
    3. Multiply any remaining factors.
  • Simplify an Expression with a Fraction Bar
    1. Simplify the expression in the numerator. Simplify the expression in the denominator.
    2. Simplify the fraction.
  • Fraction Addition and Subtraction: If [latex]a,b,\;\text{and}\;c[/latex] are numbers where [latex]c\ne 0[/latex], then [latex]\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}[/latex] and [latex]\frac{a}{c}-\frac{b}{c}=\frac{a-b}{c}[/latex].
     To add or subtract fractions, add or subtract the numerators and place the result over the common denominator.
  • Strategy for Adding or Subtracting Fractions
    1. Do they have a common denominator?
       Yes—go to step 2.
       No—Rewrite each fraction with the LCD (Least Common Denominator). Find the LCD. Change each fraction into an equivalent fraction with the LCD as its denominator.
    2. Add or subtract the fractions.
    3. Simplify, if possible. To multiply or divide fractions, an LCD IS NOT needed. To add or subtract fractions, an LCD IS needed.
  • Simplify Complex Fractions
    1. Simplify the numerator.
    2. Simplify the denominator.
    3. Divide the numerator by the denominator. Simplify if possible.

Self Check

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Glossary

complex fraction
A complex fraction is a fraction in which the numerator or the denominator contains a fraction.
denominator
The denominator is the value on the bottom part of the fraction that indicates the number of equal parts into which the whole has been divided.
equivalent fractions
Equivalent fractions are fractions that have the same value.
fraction
A fraction is written [latex]\frac{a}{b}[/latex], where [latex]b\ne 0[/latex] [latex]a[/latex] is the numerator and [latex]b[/latex] is the denominator. A fraction represents parts of a whole. The denominator [latex]b[/latex] is the number of equal parts the whole has been divided into, and the numerator [latex]a[/latex] indicates how many parts are included.
numerator
The numerator is the value on the top part of the fraction that indicates how many parts of the whole are included.
reciprocal
The reciprocal of [latex]\frac{a}{b}[/latex] is [latex]\frac{b}{a}[/latex]. A number and its reciprocal multiply to one: [latex]\frac{a}{b}·\frac{b}{a}=1[/latex].
simplified fraction
A fraction is considered simplified if there are no common factors in its numerator and denominator.
least common denominator
The least common denominator (LCD) of two fractions is the Least common multiple (LCM) of their denominators.
definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Fanshawe Pre-Health Sciences Mathematics 1 Copyright © 2022 by Domenic Spilotro, MSc is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book