3.1 Solve Equations Using the Subtraction and Addition Properties of Equality
Learning Objectives
By the end of this section, you will be able to:
- Verify a solution of an equation
- Solve equations using the Subtraction and Addition Properties of Equality
- Solve equations that require simplification
- Translate to an equation and solve
- Translate and solve applications
Try It
Before you get started, take this readiness quiz:
1) Evaluate [latex]x+4[/latex] when [latex]x=-3[/latex].
2) Evaluate [latex]15-y[/latex] when [latex]y=-5[/latex].
3) Simplify [latex]4(4n+1)-15n[/latex].
4) Translate into algebra “[latex]5[/latex] is less than [latex]x[/latex]”.
Verify a Solution of an Equation
Solving an equation is like discovering the answer to a puzzle. The purpose in solving an equation is to find the value or values of the variable that make each side of the equation the same – so that we end up with a true statement. Any value of the variable that makes the equation true is called a solution to the equation. It is the answer to the puzzle!
Solution of an equation
A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
HOW TO
To determine whether a number is a solution to an equation.
- Substitute the number in for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting equation is true (the left side is equal to the right side)
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
Example 3.1.1
Determine whether [latex]x=\frac{3}{2}[/latex] is a solution of [latex]4x-2=2x+1[/latex].
Solution
Since a solution to an equation is a value of the variable that makes the equation true, begin by substituting the value of the solution for the variable.
Step 1: Substitute [latex]\frac32[/latex] for [latex]x[/latex].
[latex]{4}\left({\color{red}{\frac32}}\right)-2\overset?=2\left({\color{red}{\frac32}}\right)+1[/latex]
Step 2: Multiply.
[latex]6-2\overset?=3+1[/latex]
Step 3: Subtract.
[latex]4=4\checkmark[/latex]
Since [latex]x=\frac{3}{2}[/latex] results in a true equation (4 is in fact equal to 4), [latex]\frac{3}{2}[/latex] is a solution to the equation [latex]4x-2=2x+1[/latex]
Try It
5) Is [latex]y=\frac{4}{3}[/latex] a solution of [latex]9y+2=6y+3?[/latex]
Solution
no
6) Is [latex]y=\frac{7}{5}[/latex] a solution of [latex]5y+3=10y-4[/latex]?
Solution
yes
Solve Equations Using the Subtraction and Addition Properties of Equality
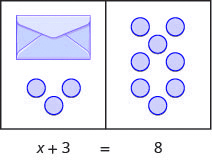
We are going to use a model to clarify the process of solving an equation. An envelope represents the variable – since its contents are unknown – and each counter represents one. We will set out one envelope and some counters on our workspace, as shown in Figure 3.1.1. Both sides of the workspace have the same number of counters, but some counters are “hidden” in the envelope. Can you tell how many counters are in the envelope?
The illustration shows a model of an equation with one variable. On the left side of the workspace is an unknown (envelope) and three counters, while on the right side of the workspace are eight counters.
What are you thinking? What steps are you taking in your mind to figure out how many counters are in the envelope?
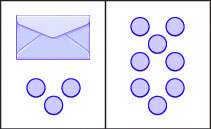
Perhaps you are thinking: “I need to remove the 3 counters at the bottom left to get the envelope by itself. The 3 counters on the left can be matched with 3 on the right and so I can take them away from both sides. That leaves five on the right—so there must be 5 counters in the envelope.” See Figure 3.1.2. for an illustration of this process.
The illustration shows a model for solving an equation with one variable. On both sides of the workspace remove three counters, leaving only the unknown (envelope) and five counters on the right side. The unknown is equal to five counters.
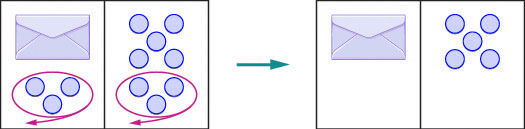
What algebraic equation would match this situation? In Figure 3.1.3 each side of the workspace represents an expression and the centre line takes the place of the equal sign. We will call the contents of the envelope [latex]x[/latex].
The illustration shows a model for the equation [latex]x+3=8[/latex].
Let’s write algebraically the steps we took to discover how many counters were in the envelope:
| [latex]x+3=8[/latex] | |
| First, we took away three from each side. | [latex]{x+3}{\color{red}{-}}{{\color{red}{3}}=8{\color{red}{-}}}{\color{red}{3}}[/latex] |
| Then we were left with five. | [latex]x=5[/latex] |
| Check: | Five in the envelope plus three more does equal eight! |
| [latex]5+3=8[/latex] |
Our model has given us an idea of what we need to do to solve one kind of equation. The goal is to isolate the variable by itself on one side of the equation. To solve equations such as these mathematically, we use the Subtraction Property of Equality.
Subtraction Property of Equality
For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex],
When you subtract the same quantity from both sides of an equation, you still have equality.
Let’s see how to use this property to solve an equation. Remember, the goal is to isolate the variable on one side of the equation. And we check our solutions by substituting the value into the equation to make sure we have a true statement.
Example 3.1.2
Solve: [latex]y+37=-13[/latex].
Solution
To get [latex]y[/latex] by itself, we will undo the addition of 37 by using the Subtraction Property of Equality.
Step 1: Subtract 37 from each side to ‘undo’ the addition.
[latex]{y+37}{\color{red}{-}}{{\color{red}{37}}=-13{\color{red}{-}}}{\color{red}{37}}[/latex]
Step 2: Simplify.
[latex]y=-50[/latex]
Step 3: Check:
[latex]y+37=-13[/latex]
Step 4: Substitute [latex]y=-50[/latex]
[latex]\begin{align*}{\color{red}{-}}{\color{red}{50}}+37&=-13\\ -13&\overset?=-13\checkmark \end{align*}[/latex]
Since [latex]y=-50[/latex] makes [latex]y+37=-13[/latex] a true statement, we have the solution to this equation.
Try It
7) Solve: [latex]x+19=-27[/latex].
Solution
[latex]x=-46[/latex]
8) Solve: [latex]x+16=-34[/latex].
Solution
[latex]x=-50[/latex]
What happens when an equation has a number subtracted from the variable, as in the equation [latex]x-5=8[/latex]? We use another property of equations to solve equations where a number is subtracted from the variable. We want to isolate the variable, so to ‘undo’ the subtraction we will add the number to both sides. We use the Addition Property of Equality.
Addition Property of Equality
For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex],
When you add the same quantity to both sides of an equation, you still have equality.
In Example 3.1.2, 37 was added to the [latex]y[/latex] and so we subtracted 37 to ‘undo’ the addition. In 3.1.3, we will need to ‘undo’ subtraction by using the Addition Property of Equality.
Example 3.1.3
Solve: [latex]a-28=-37[/latex].
Solution
Step 1: Add 28 to each side to ‘undo’ the subtraction.
[latex]{a-28}{\color{red}{+}}{{\color{red}{28}}=-37{\color{red}{+}}}{\color{red}{28}}[/latex]
Step 2: Simplify.
[latex]a=-9[/latex]
Step 3: Check:
[latex]a-28=-37[/latex]
Step 4: Substitute [latex]a=-9[/latex]
[latex]\begin{align*}{\color{red}{-}}{\color{red}{9}}-28&=37\\ -37&\overset?=-37\checkmark \end{align*}[/latex]
The solution to [latex]a-28=-37[/latex] is [latex]a=-9[/latex].
Try It
9) Solve: [latex]n-61=-75[/latex].
Solution
[latex]n=-14[/latex]
10) Solve: [latex]p-41=-73[/latex].
Solution
[latex]p=-32[/latex]
Example 3.1.4
Solve: [latex]x-\frac{5}{8}=\frac{3}{4}[/latex]
Solution
Step 1: Use the Addition Property of Equality.
[latex]{x-\frac58}{\color{red}{+}}{{\color{red}{\frac58}}=\frac68{\color{red}{+}}}{\color{red}{\frac58}}{}[/latex]
Step 2: Find the LCD to add the fractions on the right.
[latex]\begin{align*}&\;&x-\frac58+\frac58&=\frac68+\frac58\\ &\text{Simplify}\;&x&=\frac{11}8\\ \end{align*}[/latex]
Step 3: Check:
[latex]x-\frac58=\frac34[/latex]
Step 4: Substitute [latex]x=\frac{11}{8}[/latex].
[latex]\begin{align*}&\;&{\color{red}{\frac{11}{8}}}-\frac58&\overset?=\frac34 \\&\text{Subtract.}\;&\frac68&\overset?=\frac34\\ &\text{Simplify.}\;&\frac34&=\frac34\checkmark \end{align*}[/latex]
The solution to [latex]x-\frac{5}{8}=\frac{3}{4}[/latex] is [latex]x=\frac{11}{8}[/latex]
Try It
11) Solve: [latex]p-\frac{2}{3}=\frac{5}{6}[/latex]
Solution
[latex]p=\frac{3}{2}[/latex]
12) Solve: [latex]q-\frac{1}{2}=\frac{5}{6}[/latex]
Solution
[latex]q=\frac{4}{3}[/latex]
The next example will be an equation with decimals.
Example 3.1.5
Solve: [latex]n-0.63=-4.2[/latex].
Solution
Step 1: Use the Addition Property of Equality.
[latex]\begin{align*}&\;&n-0.63{\color{red}{+}}{\color{red}{0}}{\color{red}{.}}{\color{red}{63}}&=-4.2{\color{red}{+}}{\color{red}{0}}{\color{red}{.}}{\color{red}{63}} \\&\text{Add.}\;&n&=-3.57\end{align*}[/latex]
Step 2: Check:
[latex]n=-3.57[/latex]
Step 3: Let [latex]n=-3.57[/latex].
[latex]\begin{align*}{\color{red}{-}}{\color{red}{3.57}}-0.63&\overset?={\color{black}{-}}{\color{black}{4}}{\color{black}{.}}{\color{black}{2}}\\ -4.2&-4.2\checkmark\end{align*}[/latex]
Try It
13) Solve: [latex]b-0.47=-2.1[/latex].
Solution
[latex]b=-1.63[/latex]
14) Solve: [latex]c-0.93=-4.6[/latex].
Solution
[latex]c=-3.67[/latex]
Solve Equations That Require Simplification
In the previous examples, we were able to isolate the variable with just one operation. Most of the equations we encounter in algebra will take more steps to solve. Usually, we will need to simplify one or both sides of an equation before using the Subtraction or Addition Properties of Equality.
You should always simplify as much as possible before you try to isolate the variable. Remember that to simplify an expression means to do all the operations in the expression. Simplify one side of the equation at a time. Note that simplification is different from the process used to solve an equation in which we apply an operation to both sides.
Example 3.1.6
Solve: [latex]9x-5-8x-6=7[/latex].
Solution
Step 1: Simplify the expressions on each side as much as possible.
Rearrange the terms, using the Commutative Property of Addition.
[latex]\begin{align*} &\text{Combine like terms.}\;&9x-5-8x-6&=7 \\ &\;&9x-8x-5-6&=7\\ &\;&x-11&=7 \end{align*}[/latex]
Notice that each side is now simplified as much as possible.
Step 2: Isolate the variable.
Now isolate [latex]x[/latex].
[latex]{\text{Undo subtraction by adding 11 to both sides.}\;x-11}{\color{red}{+}}{{\color{red}{11}}=7{\color{red}{+}}}{\color{red}{11}}{}[/latex]
Step 3: Simplify the expressions on both sides of the equation.
[latex]x=18[/latex]
Step 4: Check the solution.
Substitute [latex]x=18[/latex]
[latex]\begin{align*} 9x-5-8x-6&=7 \\ 9{\color{red}{\left(18\right)}}{-5-8}{\color{red}{\left(8\right)}}-6&\overset?=7\\ 162-5-144-6&\overset?=7\\ 157-144&\overset?=7\\ 13-6&\overset?=7\\ 7&=7\checkmark \end{align*}[/latex]
The solution to [latex]9x-5-8x-6=7[/latex] is [latex]x=18[/latex]
Try It
15) Solve: [latex]8y-4-7y-7=4[/latex].
Solution
[latex]y=15[/latex]
16) Solve: [latex]6z+5-5z-4=3[/latex].
Solution
[latex]z=2[/latex]
Example 3.1.7
Solve: [latex]5(n-4)-4n=-8[/latex].
Solution
We simplify both sides of the equation as much as possible before we try to isolate the variable.
Step 1: Distribute on the left.
[latex]5n-20-4n=-8[/latex]
Step 2: Use the Commutative Property to rearrange terms.
[latex]\begin{align*} &\;&5n-4n-20&=-8\\ &\text{Combine like terms.}\;&n-20&=-8\\ \end{align*}[/latex]
Step 3: Each side is as simplified as possible. Next, isolate [latex]n[/latex].
Step 4: Undo subtraction by using the Addition Property of Equality.
[latex]\begin{align*} &\;&n-20{\color{red}{+}}{\color{red}{20}}&=-8{\color{red}{+}}{\color{red}{20}}\\ &\text{Add.}\;&n&=12\\\end{align*}[/latex]
Step 5: Check.
Substitute [latex]n=12[/latex].
[latex]\begin{align*} 5(n-4)-4n&=-8 \\ 5({\color{red}{12}}-4)-4({\color{red}{12}})&\overset?=-8\\ 5(8)-48&\overset?=-8\\ 40-48&\overset?=-8\\ -8&=-8\checkmark \end{align*}[/latex]
The solution to [latex]5(n-4)-4n=-8[/latex] is [latex]n=12[/latex].
Try It
17) Solve: [latex]5(p-3)-4p=-10[/latex].
Solution
[latex]p=5[/latex]
18) Solve: [latex]4(q+2)-3q=-8[/latex].
Solution
[latex]q=-16[/latex]
Example 3.1.8
Solve: [latex]3(2y-1)-5y=2(y+1)-2(y+3)[/latex].
Solution
We simplify both sides of the equation before we isolate the variable.
Step 1: Distribute on both sides.
[latex]6y-3-5y=2y+2-2y-6[/latex]
Step 2: Use the Commutative Property of Addition.
[latex]\begin{align*} &\;&6y-5y-3&=2y-2y+2-6\\ &\text{Combine like terms.}\;&y-3&=-4\\ \end{align*}[/latex]
Step 3: Each side is as simplified as possible. Next, isolate [latex]y[/latex].
Step 4: Undo subtraction by using the Addition Property of Equality.
[latex]\begin{align*} &\;&y-3{\color{red}{+}}{\color{red}{3}}&=-4{\color{red}{+}}{\color{red}{3}}\\ &\text{Add.}\;&y&=-1\end{align*}[/latex]
Step 5: Check.
Let [latex]y=-1[/latex].
[latex]\begin{align*} 3(2y-1)-5y&=2(y+1)-2(y+3) \\ 3(2({\color{red}{12}}-1)-1)-5({\color{red}{-1}})&\overset?=2(-1+1)-2(-1+3)\\ 3(-2-1)+5&\overset?=2(0)-2(2)\\ 3(-3)+5&\overset?=-4\\ -9+5&=-4\\ -4&=-4\checkmark \end{align*}[/latex]
The solution to [latex]3(2y-1)-5y=2(y+1)-2(y+3)[/latex] is [latex]y=-1[/latex].
Try It
19) Solve: [latex]4(2h-3)-7h=6(h-2)-6(h-1)[/latex]
Solution
[latex]h=6[/latex]
20) Solve: [latex]2(5x+2)-9x=3(x-2)-3(x-4)[/latex]
Solution
[latex]x=2[/latex]
Translate to an Equation and Solve
To solve applications algebraically, we will begin by translating from English sentences into equations. Our first step is to look for the word (or words) that would translate to the equals sign. Below table shows us some of the words that are commonly used.
| Equals = | is is equal to is the same as the result is gives was will be |
|---|
The steps we use to translate a sentence into an equation are listed below.
HOW TO
Translate an English sentence to an algebraic equation.
- Locate the “equals” word(s). Translate to an equals sign (=).
- Translate the words to the left of the “equals” word(s) into an algebraic expression.
- Translate the words to the right of the “equals” word(s) into an algebraic expression.
Example 3.1.9
Translate and solve: Eleven more than [latex]x[/latex] is equal to 54.
Solution
Step 1: Translate.
[latex]\underbrace{Eleven\;more\;than\;x}_{x+11}\;\underbrace{is\;equal\;to}_=\;\underbrace{54}_{54}[/latex]
Step 2: Subtract 11 from both sides.
[latex]{x+11}{\color{red}{-}}{{\color{red}{11}}=54{\color{red}{-}}}{\color{red}{11}}[/latex]
Step 3: Simplify.
[latex]x=43[/latex]
Step 4: Check
[latex]\begin{align*}43+11&\overset?=54\\54&=54\end{align*}[/latex]
Try It
21) Translate and solve: Ten more than [latex]x[/latex] is equal to 41.
Solution
[latex]x+10=41[/latex]; [latex]x=31[/latex]
22) Translate and solve: Twelve less than [latex]x[/latex] is equal to 51.
Solution
[latex]y-12=51[/latex]; [latex]y=63[/latex]
Example 3.1.10
Translate and solve: The difference of [latex]12t[/latex] and [latex]11t[/latex] is [latex]-14[/latex].
Solution
Step 1: Translate.
[latex]\underbrace{The\;difference\;of\;12t\;and\;11t}_{12t-11t}\;\underbrace{is\;}_=\;\underbrace{-14}_{-14}[/latex]
Step 2: Simplify.
[latex]t=-14[/latex]
Step 3: Check:
[latex]\begin{align*} 12(-14)-11(-14)&\overset?=-14\\ (-168+154)&\overset?=-14\\ -14&=-14 \end{align*}[/latex]
Try It
23) Translate and solve: The difference of [latex]4x[/latex] and [latex]3x[/latex] is [latex]14[/latex].
Solution
[latex]\begin{align*}4x-3x&=14\\x&=14\end{align*}[/latex]
24) Translate and solve: The difference of [latex]7a[/latex] and [latex]6a[/latex] is [latex]-8[/latex].
Solution
[latex]\begin{align*}7a-6a&=-8\\a&=-8\end{align*}[/latex]
Translate and Solve Applications
Most of the time a question that requires an algebraic solution comes out of a real-life question. To begin with, that question is asked in English (or the language of the person asking) and not in math symbols. Because of this, it is an important skill to be able to translate an everyday situation into algebraic language.
We will start by restating the problem in just one sentence, assigning a variable, and then translating the sentence into an equation to solve. When assigning a variable, choose a letter that reminds you of what you are looking for. For example, you might use [latex]q[/latex] for the number of quarters if you were solving a problem about coins.
Example 3.1.11
The MacIntyre family recycled newspapers for two months. The two months of newspapers weighed a total of 57 pounds. The second month, the newspapers weighed 28 pounds. How much did the newspapers weigh the first month?
Solution
Step 1: Read the problem.
Make sure all the words and ideas are understood.
The problem is about the weight of newspapers.
Step 2: Identify what we are asked to find.
What are we asked to find?
“How much did the newspapers wight the 2nd month?”
Step 3: Name what we are looking for.
Choose a variable to represent that quantity.
Let [latex]w[/latex] = weight of the newspapers the 1st month
Step 4: Translate into an equation.
It may be helpful to restate the problem in one sentence with the important information.
Restate the problem.
Weight of newspapers the 1st month plus the weight of the newspapers the 2nd month equals 57 pounds.
We know the weight of the newspapers the second month is 28 pounds.
Weight from 1st month plus 2nd month equals 57 pounds.
Translate into an equation, using the variable [latex]w[/latex].
[latex]w+28=57[/latex]
Step 5: Solve the equation using good algebra techniques.
[latex]\begin{align*}w+28{\color{red}{-}}{\color{red}{28}}&=57{\color{red}{-}}{\color{red}{28}}\\ w&=29 \end{align*}[/latex]
Step 6: Check the answer in the problem and make sure it makes sense.
Does 1st month’s weight plus 2nd month’s weight equal 57 pounds?
[latex]\begin{align*} 29+28&\overset?=57\\ 57&=57\checkmark \end{align*}[/latex]
Step 7: Answer the question with a complete sentence.
Write a sentence to answer “How much did the newspapers weigh the 2nd month?”
The 2nd month the newspapers weighed 29 pounds.
Translate into an algebraic equation and solve:
HOW TO
Solve an application.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with the important information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Example 3.1.12
Randell paid [latex]\$28,675[/latex] for his new car. This was [latex]\$875[/latex] less than the sticker price. What was the sticker price of the car?
Solution
Step 1: Read the problem.
Step 2: Identify what we are looking for.
“What was the sticker price of the car?”
Step 3: Name what we are looking for.
Choose a variable to represent that quantity.
Let [latex]s[/latex] = the sticker price of the car.
Step 4: Translate into an equation. Restate the problem in one sentence.
[latex]\$28,675[/latex] is [latex]\$875[/latex] less than the sticker price
[latex]\$28,675[/latex] is [latex]\$875[/latex] less than [latex]s[/latex]
Step 5: Solve the equation.
[latex]\begin{align*} 28675&=s-875\\ 28675+875&=s-875+875\\ 29550&=s \end{align*}[/latex]
Step 6: Check the answer.
Is [latex]\$875[/latex] less than [latex]\$29,550[/latex]? Equal to [latex]\$28,675[/latex]?
[latex]\begin{align*}29,550-875&\overset?=28,675\\28,675&=28,675\end{align*}[/latex]
Step 7: Answer the question with a complete sentence.
The sticker price of the car was [latex]\$29,550[/latex].
Try It
25) Translate into an algebraic equation and solve:
The Pappas family has two cats, Zeus and Athena. Together, they weigh 23 pounds. Zeus weighs 16 pounds. How much does Athena weigh?
Solution
7 pounds
26) Translate into an algebraic equation and solve:
Sam and Henry are roommates. Together, they have 68 books. Sam has 26 books. How many books does Henry have?
Solution
42 books
27) Translate into an algebraic equation and solve:
Eddie paid $19,875 for his new car. This was $1,025 less than the sticker price. What was the sticker price of the car?
Solution
$20,900
28) Translate into an algebraic equation and solve:
The admission price for the movies during the day is $7.75. This is $3.25 less the price at night. How much does the movie cost at night?
Solution
$11.00
Key Concepts
- To Determine Whether a Number is a Solution to an Equation
- Substitute the number in for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting statement is true.
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
- Addition Property of Equality
- For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], then [latex]a+c=b+c[/latex].
- Subtraction Property of Equality
- For any numbers
- [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], then [latex]a-c=b-c[/latex].
- To Translate a Sentence to an Equation
- Locate the “equals” word(s). Translate to an equal sign ([latex]=[/latex]).
- Translate the words to the left of the “equals” word(s) into an algebraic expression.
- Translate the words to the right of the “equals” word(s) into an algebraic expression.
- To Solve an Application
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with the important information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Self Check
After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Glossary
- solution of an equation
- solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.