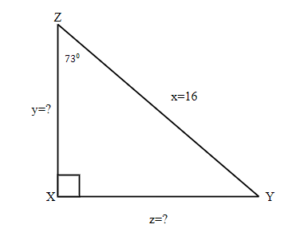Exercises: Sine, Cosine and Tangent Ratios and Applications of Trigonometry (6.5)

Domenic Spilotro, MSc

Exercises: Sine, Cosine and Tangent Ratios and Applications of Trigonometry (6.5)

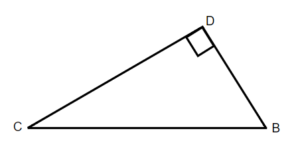
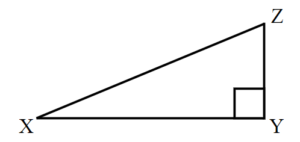
Exercises: Label Sides of Triangles

Instructions: For questions 1-2, label the sides of the triangle.

1.

A right triangle is shown with angles B, C, and right angle D. — Figure 6.P.5.1

Solution

A right triangle is shown with sides b, c, and d. Angle B is opposite side b, angle C is opposite side c, and angle D is opposite side D. — Figure 6.P.5.2

2.

A right triangle is shown with angles X, Z, and right angle Y. — Figure 6.P.5.3

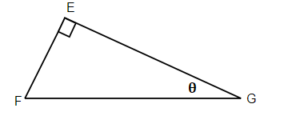
Exercises: Finding Adjacent or Opposite Sides

Instructions: For questions 3-4, solve.

3. If the reference angle in Question 1 is B, Find the adjacent?

Solution

c

4. If the reference angle in Question 2 is Z, find the opposite?

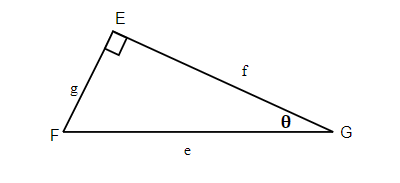
Exercises: Label and Find Sides of a Triangle

Instructions: For questions 5-6, label the sides of the triangle and find the hypotenuse, opposite and adjacent.

5.

A right triangle is shown with angles F, G, and right angle E. Angle G is equal to theta. — Figure 6P.5.4

Solution

g is opposite , f is adjacent, and e is hypotenuse

A right triangle is shown with sides e, f, and g, and angles E, F, and G. Angle E is opposite side e, angle F is opposite side f, and angle G is opposite side g. — Figure 6P.5.5

6.

Exercises: Find the Given Ratios

Instructions: For questions 7-10, use your calculator to find the given ratios. Round to four decimal places if necessary.

7. [latex]\sin {47}^{\circ}[/latex]

Solution

[latex]0.7314[/latex]

8. [latex]\cos {82}^{\circ}[/latex]

9. [latex]\tan {12}^{\circ}[/latex]

Solution

[latex]0.2126[/latex]

10. [latex]\sin {30}^{\circ}[/latex]

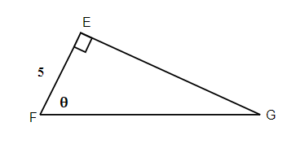
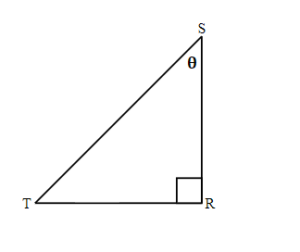
Exercises: Find the Sine, Cosine, and Tangent of [latex]{\color{White}{\theta}}[/latex]

Instructions: For the given triangles in questions 11-14, find the sine, cosine and tangent of the [latex]\theta[/latex].

11.

Solution

[latex]\text{sin }\theta=\frac{g}{e},\;\text{cos }\theta=\frac{f}{e},\;\text{tan }\theta=\frac{g}{f}[/latex]

12.

A right triangle with angles F, G, and right angle E is shown. Angle F is equal to theta. — Figure 6P.5.9

13.

A right triangle is shown with angles T, S, and right angle R. Angle S is equal to theta. — Figure 6P.5.10

Solution

[latex]\text{sin }\theta=\frac{s}{r},\;\text{cos }\theta=\frac{t}{r},\;\text{tan }\theta=\frac{s}{t}[/latex]

14.

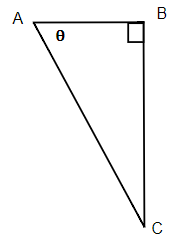
A right triangle is shown with angles A, C, and right angle B. Angle A is equal to theta. — Figure 6P.5.11

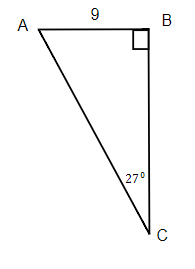
Exercises: Find the Missing Side

Instructions: For the given triangles in questions 15-18, find the missing side. Round it to one decimal place.

15. Find the hypotenuse.

A right triangle is shown with angles A, C, and right angle B. Angle C is equal to 27 degrees and side AB equals 9 units. — Figure 6P.5.12

Solution

[latex]b=19.8[/latex]

16. Find [latex]b[/latex] if [latex]a=6[/latex].

A right triangle is shown with angles A, C, and right angle B. Angle C is equal to twenty-seven degrees. — Figure 6P.5.13

17. Find the opposite.

A right triangle with angles B, D, and right angle C is shown. Angle C is equal to thirty-nine degrees and side BC is equal to nineteen units. — Figure 6P.5.14

Solution

[latex]c=12[/latex]

18. Find the adjacent.

A right triangle is shown with angles B, C, and right angle D. Angle B is equal to fifty-seven degrees and side BC is equal to 40 units. — Figure 6P.5.15

Exercises: Find the Missing Sides

Instructions: For the given triangles in questions 19-20, find the missing sides. Round it to one decimal place.

19.

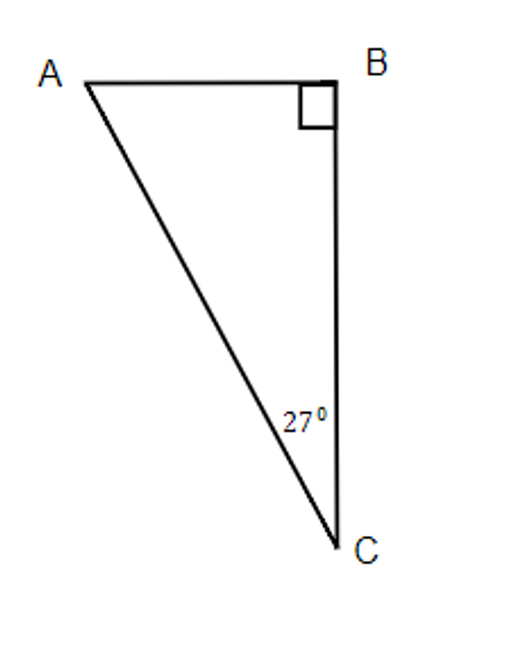
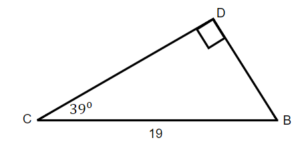
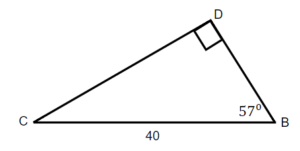
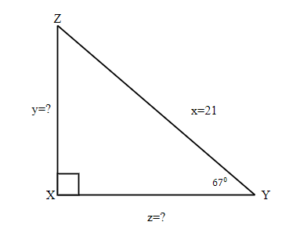
A right triangle is shown with angles Y, Z, and right angle X. Angle Y equals sixty-seven degrees. Side x equals 21 units. Sides y and z have an unknown length. — Figure 6P.5.16

Solution

[latex]y=19.3,\;z=8.2[/latex]

20.

A right triangle is shown with angles Y, Z, and right angle X. Angle Z equals seventy-three degrees. Side x equals 16 units. Sides y and z have an unknown length. — Figure 6P.5.17

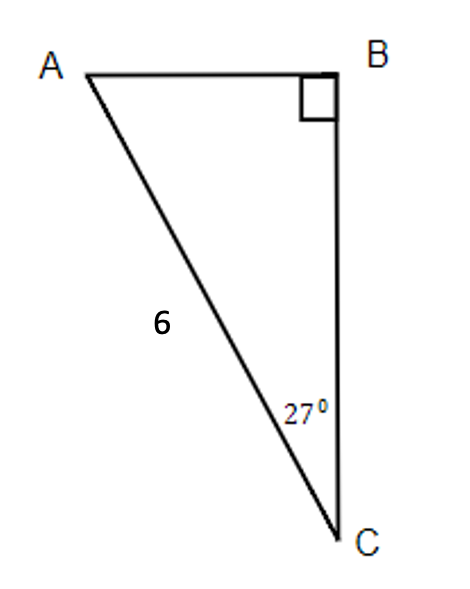
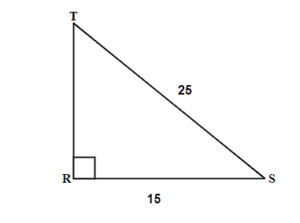
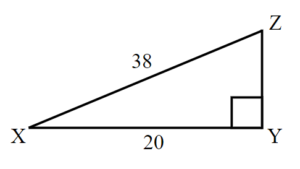
Exercises: Solve Triangles

Instructions: For questions 21-24, solve the triangles. Round to one decimal place.

21.

A right triangle is shown with angles B, C, and right angle D. Angle C equals sixty-seven degrees. Side d equals 44 units. — Figure 6P.5.18

Solution

[latex]\angle B=61^\circ,\;\angle C= 29^\circ,\;\angle D=90^\circ,\;b=38.5,\;c=21.3,\;d=44[/latex]

22.

A right triangle is shown with angles A, C, and right angle B. Angle C equals twenty-seven degrees and side b equals 6 units. — Figure 6P.5.19

23.

A right triangle is shown with angles S, T, and right angle R. Side r equals twenty-five units and side T equals fifteen units. — Figure 6P.5.20

Solution

[latex]\angle T=36.9^\circ,\;\angle R=90^\circ,\;\angle S=53.1^\circ,\;t=15,\;r=25,\;s=20[/latex]

24.

A right triangle is shown with angles X,Z, and right angle Y. Side y equals thirty-eight units and side z equals twenty units. — Figure 6P.5.21

Exercises: Word Problems

Instructions: For questions 25-30, answer the given word problems.

25. Kim stands [latex]75[/latex] metres from the bottom of a tree and looks up at the top of the tree at a [latex]48^\circ[/latex] angle. How tall is the tree?

Solution

[latex]83.3[/latex] m

26. A tree makes a shadow that is [latex]6[/latex] metres long when the angle of elevation to the sun is [latex]52^\circ[/latex]. How tall is the tree?

27. A ladder that is [latex]15[/latex] feet is leaning against a house and makes a [latex]45^\circ[/latex] angle with the ground. How far is the base of the ladder from the house?

Solution

[latex]10.6[/latex] ft

28. Roxanne is flying a kite and has let out [latex]100[/latex] feet of string. The angle of elevation with the ground is [latex]38^\circ[/latex]. How high is her kite above the ground?

29. Marta is flying a kite and has let out [latex]28[/latex] metres of string. If the kite is [latex]10[/latex] metres above the ground, what is the angle of elevation?

Solution

[latex]20.9^\circ[/latex]

30. An airplane takes off from the ground at the angle of [latex]25^\circ[/latex]. If the airplane traveled [latex]200[/latex] kilometres, how high above the ground is it?

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Fanshawe Pre-Health Sciences Mathematics 1 Copyright © 2022 by Domenic Spilotro, MSc is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

License

Share This Book