"

Exercises: Graph Linear Equations in Two Variables (3.9)

Exercises: Plot Points in a Rectangular Coordinate System

Instructions: For questions 1-8, plot each point in a rectangular coordinate system and identify the quadrant in which the point is located.

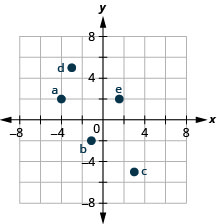
1.

a.[latex](-4,2)[/latex]
b.[latex](-1,-2)[/latex]
c.[latex](3,-5)[/latex]
d.[latex](-3,5)[/latex]
e.[latex]\left(\frac{5}{3},2\right)[/latex]

Solution
The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (negative 4, 2) is plotted and labeled "a". The point (negative 1, negative 2) is plotted and labeled "b". The point (3, negative 5) is plotted and labeled "c". The point (negative 3, 5) is plotted and labeled “d”. The point (5 thirds, 2) is plotted and labeled “e”.
Figure P3.9.1

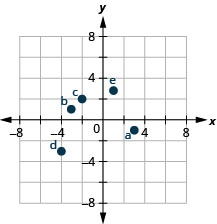
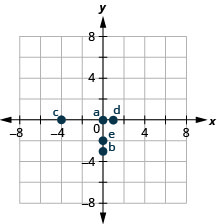
2.

a.[latex](-2,-3)[/latex]
b.[latex](3,-3)[/latex]
c.[latex](-4,1)[/latex]
d.[latex](4,-1)[/latex]
e.[latex]\left(\frac{3}{2},1\right)[/latex]

3.

a.[latex](3,-1)[/latex]
b.[latex](-3,1)[/latex]
c.[latex](-2,2)[/latex]
d.[latex](-4,-3)[/latex]
e.[latex]\left(1,\frac{14}{5}\right)[/latex]

Solution
The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (3, negative 1) is plotted and labeled "a". The point (negative 3, 1) is plotted and labeled "b". The point (negative 2, 2) is plotted and labeled "c". The point (negative 4, negative 3) is plotted and labeled “d”. The point (1, 14 fifths) is plotted and labeled “e”.
Figure P3.9.2

4.

a.[latex](-1,1)[/latex]
b.[latex](-2,-1)[/latex]
c.[latex](2,1)[/latex]
d.[latex](1,-4)[/latex]
e.[latex]\left(3,\frac{7}{2}\right)[/latex]

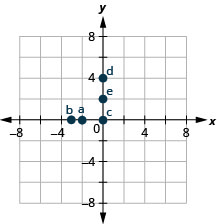
5.

a.[latex]\left(-2,0\right)[/latex]
b.[latex]\left(-3,0\right)[/latex]
c.[latex]\left(0,0\right)[/latex]
d.[latex]\left(0,4\right)[/latex]
e.[latex]\left(0,2\right)[/latex]

Solution
The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (negative 2, 0) is plotted and labeled "a". The point (negative 3, 0) is plotted and labeled "b". The point (0, 0) is plotted and labeled "c". The point (0, 4) is plotted and labeled “d”. The point (0, 3) is plotted and labeled “e”.
Figure 3P.9.3

6.

a.[latex]\left(0,1\right)[/latex]
b.[latex]\left(0,-4\right)[/latex]
c.[latex]\left(-1,0\right)[/latex]
d.[latex]\left(0,0\right)[/latex]
e.[latex]\left(5,0\right)[/latex]

7.

a.[latex]\left(0,0\right)[/latex]
b.[latex]\left(0,-3\right)[/latex]
c.[latex]\left(-4,0\right)[/latex]
d.[latex]\left(1,0\right)[/latex]
e.[latex]\left(0,-2\right)[/latex]

Solution
The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (0, 0) is plotted and labeled "a". The point (0, negative 3) is plotted and labeled "b". The point (negative 4, 0) is plotted and labeled "c". The point (1, 0) is plotted and labeled “d”. The point (0, negative 2) is plotted and labeled “e”.
Figure 3P.9.4

8.

a.[latex]\left(-3,0\right)[/latex]
b.[latex]\left(0,5\right)[/latex]
c.[latex]\left(0,-2\right)[/latex]
d.[latex]\left(2,0\right)[/latex]
e.[latex]\left(0,0\right)[/latex]

Exercises: Name Ordered Pairs in a Rectangular Coordinate System

Instructions: For questions 9-12, name the ordered pair of each point shown in the rectangular coordinate system.

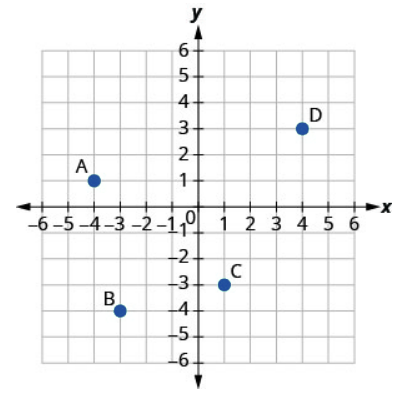
9.

The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (negative 4, 1) is plotted and labeled “A”. The point (negative 3, negative 4) is plotted and labeled “B”. The point (1, negative 3) is plotted and labeled “C”. The point (4, 3) is plotted and labeled “D”.
Figure 3P.9.5
Solution

A: [latex](-4,1)[/latex]
B: [latex](-3,-4)[/latex]
C: [latex](1,-3)[/latex]
D: [latex](4,3)[/latex]

10.

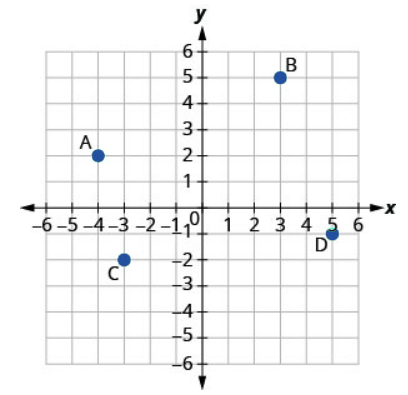
The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The point (negative 4, 2) is plotted and labeled “A”. The point (3, 5) is plotted and labeled “B”. The point (negative 3, negative 2) is plotted and labeled “C”. The point (5, negative 1) is plotted and labeled “D”.
Figure 3P.9.6

11.

The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (0, negative 2) is plotted and labeled “A”. The point (negative 2, 0) is plotted and labeled “B”. The point (0, 5) is plotted and labeled “C”. The point (5, 0) is plotted and labeled “D”.
Figure 3P.9.7
Solution

A: [latex](0,-2)[/latex]
B: [latex](-2,0)[/latex]
C: [latex](0,5)[/latex]
D: [latex](5,0)[/latex]

12.

The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (0, negative 1) is plotted and labeled “A”. The point (negative 1, 0) is plotted and labeled “B”. The point (4, 0) is plotted and labeled “C”. The point (0, 4) is plotted and labeled “D”.
Figure 3P.9.8

Exercises: Verify Solutions to an Equation in Two Variables

Instructions: For questions 13-20, which ordered pairs are solutions to the given equations?

13. [latex]2x+y=6[/latex]

a.[latex](1,4)[/latex]
b.[latex](3,0)[/latex]
c.[latex](2,3)[/latex]

Solution

a, b

14. [latex]x+3y=9[/latex]

a.[latex](0,3)[/latex]
b.[latex](6,1)[/latex]
c.[latex](-3,-3)[/latex]

15. [latex]4x-2y=8[/latex]

a.[latex](3,2)[/latex]
b.[latex](1,4)[/latex]
c.[latex](0,-4)[/latex]

Solution

a, c

16. [latex]3x-2y=12[/latex]

a.[latex](4,0)[/latex]
b.[latex](2,-3)[/latex]
c.[latex](1,6)[/latex]

17. [latex]y=4x+3[/latex]

a.[latex](4,3)[/latex]
b.[latex](-1,-1)[/latex]
c.[latex]\left(\frac{1}{2},5\right)[/latex]

Solution

b, c

18. [latex]y=2x-5[/latex]

a.[latex](0,-5)[/latex]
b.[latex](2,1)[/latex]
c.[latex]\left(\frac{1}{2},-4\right)[/latex]

19. [latex]y=\frac{1}{2}x-1[/latex]

a.[latex](2,0)[/latex]
b.[latex](-6,-4)[/latex]
c.[latex](-4,-1)[/latex]

Solution

a, b

20. [latex]y=\frac{1}{3}x+1[/latex]

a.[latex](-3,0)[/latex]
b.[latex](9,4)[/latex]
c.[latex](-6,-1)[/latex]

Exercises: Complete a Table of Solutions to a Linear Equation

Instructions: For questions 21-32, complete the table to find solutions to each linear equation.

21. [latex]y=2x-4[/latex]

[latex]x[/latex] [latex]y[/latex] [latex](x,y)[/latex]
[latex]0[/latex]
[latex]2[/latex]
[latex]-1[/latex]
Solution
[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex] [latex]-4[/latex] [latex]\left(0,-4\right)[/latex]
[latex]2[/latex] [latex]0[/latex] [latex]\left(2,0\right)[/latex]
[latex]-1[/latex] [latex]-6[/latex] [latex]\left(-1,-6\right)[/latex]

22. [latex]y=3x-1[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]2[/latex]
[latex]-1[/latex]

23. [latex]y=-x+5[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]3[/latex]
[latex]-2[/latex]
Solution
[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex] [latex]5[/latex] [latex]\left(0,5\right)[/latex]
[latex]3[/latex] [latex]2[/latex] [latex]\left(3,2\right)[/latex]
[latex]-2[/latex] [latex]7[/latex] [latex]\left(-2,7\right)[/latex]

24. [latex]y=-x+2[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]3[/latex]
[latex]-2[/latex]

25. [latex]y=\frac{1}{3}x+1[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]3[/latex]
[latex]6[/latex]
Solution
[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex] [latex]1[/latex] [latex]\left(0,1\right)[/latex]
[latex]3[/latex] [latex]2[/latex] [latex]\left(3,2\right)[/latex]
[latex]6[/latex] [latex]3[/latex] [latex]\left(6,3\right)[/latex]

26. [latex]y=\frac{1}{2}x+4[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]2[/latex]
[latex]4[/latex]

27. [latex]y=-\frac{3}{2}x-2[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]2[/latex]
[latex]-2[/latex]
Solution
[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex] [latex]-2[/latex] [latex]\left(0,-2\right)[/latex]
[latex]2[/latex] [latex]-5[/latex] [latex]\left(2,-5\right)[/latex]
[latex]-2[/latex] [latex]1[/latex] [latex]\left(-2,1\right)[/latex]

28. [latex]y=-\frac{2}{3}x-1[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]3[/latex]
[latex]-3[/latex]

29. [latex]x+3y=6[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]3[/latex]
[latex]0[/latex]
Solution
[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex] [latex]2[/latex] [latex]\left(0,2\right)[/latex]
[latex]3[/latex] [latex]4[/latex] [latex]\left(3,1\right)[/latex]
[latex]6[/latex] [latex]0[/latex] [latex]\left(6,0\right)[/latex]

30. [latex]x+2y=8[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]4[/latex]
[latex]0[/latex]

31. [latex]2x-5y=10[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]10[/latex]
[latex]0[/latex]
Solution
[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex] [latex]-2[/latex] [latex]\left(0,-2\right)[/latex]
[latex]10[/latex] [latex]2[/latex] [latex]\left(10,2\right)[/latex]
[latex]5[/latex] [latex]0[/latex] [latex]\left(5,0\right)[/latex]

32. [latex]3x-4y=12[/latex]

[latex]x[/latex] [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex]
[latex]8[/latex]
[latex]0[/latex]

Exercises: Find Solutions to a Linear Equation

Instructions: For questions 33-48, find three solutions to each linear equation.

33. [latex]y=5x-8[/latex]

Solution

Answers will vary.

34. [latex]y=3x-9[/latex]
35. [latex]y=-4x+5[/latex]
Solution

Answers will vary.

36. [latex]y=-2x+7[/latex]
37. [latex]x+y=8[/latex]
Solution

Answers will vary.

38. [latex]x+y=6[/latex]
39. [latex]x+y=-2[/latex]
Solution

Answers will vary.

40. [latex]x+y=-1[/latex]
41. [latex]3x+y=5[/latex]
Solution

Answers will vary.

42. [latex]2x+y=3[/latex]
43. [latex]4x-y=8[/latex]
Solution

Answers will vary.

44. [latex]5x-y=10[/latex]
45. [latex]2x+4y=8[/latex]
Solution

Answers will vary.

46. [latex]3x+2y=6[/latex]
47. [latex]5x-2y=10[/latex]
Solution

Answers will vary.

48. [latex]4x-3y=12[/latex]

Exercises: Recognize the Relationship Between the Solutions of an Equation and its Graph

Instructions: For questions 49-52, for each ordered pair, decide:

a. Is the ordered pair a solution to the equation?
b. Is the point on the line?

49. [latex]y=x+2[/latex]

a.[latex]\left(0,2\right)[/latex]
b.[latex]\left(1,2\right)[/latex]
c.[latex]\left(-1,1\right)[/latex]
d.[latex]\left(-3,-1\right)[/latex]

The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, negative 4), (negative 5, negative 3), (negative 4, negative 2), (negative 3, negative 1), (negative 2, 0), (negative 1, 1), (0, 2), (1, 3), (2, 4), (3, 5), (4, 6), and (5, 7).
Figure 3P.9.9
Solution

a. yes; no
b. no; no
c. yes; yes
d. yes; yes

50. [latex]y=x-4[/latex]

a.[latex]\left(0,-4\right)[/latex]
b.[latex]\left(3,-1\right)[/latex]
c.[latex]\left(2,2\right)[/latex]
d.[latex]\left(1,-5\right)[/latex]

The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 3, negative 7), (negative 2, negative 6), (negative 1, negative 5), (0, negative 4), (1, negative 3), (2, negative 2), (3, negative 1), (4, 0), (5, 1), (6, 2), and (7, 3).
Figure 3P.9.10

51. [latex]y=\frac{1}{2}x-3[/latex]

a.[latex]\left(0,-3\right)[/latex]
b.[latex]\left(2,-2\right)[/latex]
c.[latex]\left(-2,-4\right)[/latex]
d.[latex]\left(4,1\right)[/latex]

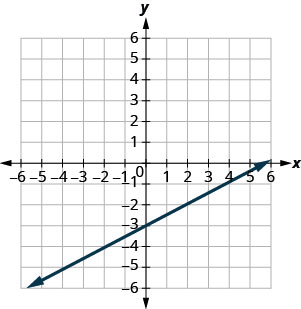
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, negative 6), (negative 4, negative 5), (negative 2, negative 4), (0, negative 3), (2, negative 2), (4, negative 1), and (6, 0).
Figure 3P.9.11
Solution

a. yes; yes
b. yes; yes
c. yes; yes
d. no; no

52. [latex]y=\frac{1}{3}x+2[/latex]

a.[latex]\left(0,2\right)[/latex]
b.[latex]\left(3,3\right)[/latex]
c.[latex]\left(-3,2\right)[/latex]
d.[latex]\left(-6,0\right)[/latex]

The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, 0), (negative 3, 1), (0, 2), (3, 3), and (6, 4).
Figure 3P.9.12

Exercises: Graph a Linear Equation by Plotting Points

Instructions: For questions 53-96, graph by plotting points.

53. [latex]y=3x-1[/latex]

Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 3, negative 10), (negative 2, negative 7), (negative 1, negative 4), (0, negative 1), (1, 2), (2, 5), and (3, 8).
Figure 3P.9.13
54. [latex]y=2x+3[/latex]
55. [latex]y=-2x+2[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 4, 10), (negative 3, 8), (negative 2, 6), (negative 1, 4), (0, 2), (1, 0), (2, negative 2), (3, negative 4), (4, negative 6), and (5, negative 8).
Figure 3P.9.14
56. [latex]y=-3x+1[/latex]
57. [latex]y=x+2[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 10, negative 8), (negative 9, negative 7), (negative 8, negative 6), (negative 7, negative 5), (negative 6, negative 4), (negative 5, negative 3), (negative 4, negative 2), (negative 3, negative 1), (negative 2, 0), (negative 1, 1), (0, 2), (1, 3), (2, 4), (3, 5), (4, 6), (5, 7), (6, 8), (7, 9), and (8, 10).
Figure 3P.9.15
58. [latex]y=x-3[/latex]
59. [latex]y=-x-3[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 10, 7), (negative 9, 6), (negative 8, 5), (negative 7, 4), (negative 6, 3), (negative 5, 2), (negative 4, 1), (negative 3, 0), (negative 2, negative 1), (negative 1, negative 2), (0, negative 3), (1, negative 4), (2, negative 5), (3, negative 6), (4, negative 7), (5, negative 8), (6, negative 9), and (7, negative 10).
Figure 3P.9.16
60. [latex]y=-x-2[/latex]
61. [latex]y=2x[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 5, negative 10), (negative 4, negative 8), (negative 3, negative 6), (negative 2, negative 4), (negative 1, negative 2), (0, 0), (1, 2), (2, 4), (3, 6), (4, 8), and (5, 10).
Figure 3P.9.17
62. [latex]y=3x[/latex]
63. [latex]y=-4x[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 3, 12), (negative 2, 8), (negative 1, 4), (0, 0), (1, negative 4), (2, negative 8), and (3, negative 12).
Figure 3P.9.18
64. [latex]y=-2x[/latex]
65. [latex]y=\frac{1}{2}x+2[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 12, negative 4), (negative 10, negative 3), (negative 8, negative 2), (negative 6, negative 1), (negative 4, 0), (negative 2, 1), (0, 2), (2, 3), (4, 4), (6, 5), (8, 6), and (10, 7).
Figure 3P.9.19
66. [latex]y=\frac{1}{3}x-1[/latex]
67. [latex]y=\frac{4}{3}x-5[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 3, negative 9), (0, negative 5), (3, negative 1), (6, 3), and (9, 7).
Figure 3P.9.20
68. [latex]y=\frac{3}{2}x-3[/latex]
69. [latex]y=-\frac{2}{5}x+1[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 10, 5), (negative 5, 3), (0, 1), (5, negative 1), and (10, negative 3).
Figure 3P.9.21
70. [latex]y=-\frac{4}{5}x-1[/latex]
71. [latex]y=-\frac{3}{2}x+2[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 6, 11), (negative 4, 8), (negative 2, 5), (0, 2), (2, negative 1), (4, negative 4), (6, negative 7), and (8, negative 10).
Figure 3P.9.22
72. [latex]y=-\frac{5}{3}x+4[/latex]
73. [latex]x+y=6[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 4, 10), (negative 3, 9), (negative 2, 8), (negative 1, 7), (0, 6), (1, 5), (2, 4), (3, 3), (4, 2), (5, 1), (6, 0), (7, negative 1), (8, negative 2), (9, negative 3), and (10, negative 4).
Figure 3P.9.23
74. [latex]x+y=4[/latex]
75. [latex]x+y=-3[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 10, 7), (negative 9, 6), (negative 8, 5), (negative 7, 4), (negative 6, 3), (negative 5, 2), (negative 4, 1), (negative 3, 0), (negative 2, negative 1), (negative 1, negative 2), (0, negative 3), (1, negative 4), (2, negative 5), (3, negative 6), (4, negative 7), (5, negative 8), (6, negative 9), and (7, negative 10).
Figure 3P.9.24
76. [latex]x+y=-2[/latex]
77. [latex]x-y=2[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 8, negative 10), (negative 7, negative 9), (negative 6, negative 8), (negative 5, negative 7), (negative 4, negative 6), (negative 3, negative 5), (negative 2, negative 4), (negative 1, negative 3), (0, negative 2), (1, negative 1), (2, 0), (3, 1), (4, 2), (5, 3), (6, 4), (7, 5), (8, 6), (9, 7), and (10, 8).
Figure 3P.9.25
78. [latex]x-y=1[/latex]
79. [latex]x-y=-1[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The straight line goes through the points (negative 9, negative 8), (negative 8, negative 7), (negative 7, negative 6), (negative 6, negative 5), (negative 5, negative 4), (negative 4, negative 3), (negative 3, negative 2), (negative 2, negative 1), (negative 1, 0), (0, 1), (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), (8, 9), and (9, 10).
Figure 3P.9.26
80. [latex]x-y=-3[/latex]
81. [latex]3x+y=7[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to -7. The equation 3 x plus y equals 7 is graphed.
Figure 3P.9.27
82. [latex]5x+y=6[/latex]
83. [latex]2x+y=-3[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 5, 7), (negative 4, 5), (negative 3, 3), (negative 2, 1), (negative 1, negative 1), (0, negative 3), (1, negative 5), and (2, negative 7).
Figure 3P.9.28
84. [latex]4x+y=-5[/latex]
85. [latex]\frac{1}{3}x+y=2[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, 4), (negative 3, 3), (0, 2), (3, 1), and (6, 0).
Figure 3P.9.29
86. [latex]\frac{1}{2}x+y=3[/latex]
87. [latex]\frac{2}{5}x-y=4[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 5, negative 2), (0, negative 4), and (5, negative 6).
Figure 3P.9.30
88. [latex]\frac{3}{4}x-y=6[/latex]
89. [latex]2x+3y=12[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 3, 6), (0, 4), (3, 2), and (6, 0).
Figure 3P.9.31
90. [latex]4x+2y=12[/latex]
91. [latex]3x-4y=12[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 4, negative 6), (0, negative 3), (4, 0), and (8, 3).
Figure 3P.9.32
92. [latex]2x-5y=10[/latex]
93. [latex]x-6y=3[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, negative three halves), (negative 3, negative 1), (0, negative one half), (3, 0), and (6, one half).
Figure 3P.9.33
94. [latex]x-4y=2[/latex]
95. [latex]5x+2y=4[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 2, 7), (0, 2), (2, negative 3), and (4, negative 8).
Figure 3P.9.34
96. [latex]3x+5y=5[/latex]

Exercises: Graph Vertical and Horizontal Lines

Instructions: For questions 97-108, graph each equation.

97. [latex]x=4[/latex]
Solution
The figure shows a straight vertical line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The vertical line goes through the points (4, 0), (4, 1), (4, 2) and all points with first coordinate 4.
Figure 3P.9.35
98. [latex]x=3[/latex]
99. [latex]x=-2[/latex]
Solution
The figure shows a straight vertical line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The vertical line goes through the points (negative 2, 0), (negative 2, 1), (negative 2, 2) and all points with first coordinate negative 2.
Figure 3P.9.36
100. [latex]x=-5[/latex]
101. [latex]y=3[/latex]
Solution
The figure shows a straight horizontal line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The horizontal line goes through the points (0, 3), (1, 3), (2, 3) and all points with second coordinate 3.
Figure 3P.9.37
102. [latex]y=1[/latex]
103. [latex]y=-5[/latex]
Solution
The figure shows a straight horizontal line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The horizontal line goes through the points (0, negative 5), (1, negative 5), (2, negative 5) and all points with second coordinate negative 5.
Figure 3P.9.38
104. [latex]y=-2[/latex]
105. [latex]x=\frac{7}{3}[/latex]
Solution
The figure shows a straight vertical line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. The vertical line goes through the points (7/3, 0), (7/3, 1), (7/3, 2) and all points with first coordinate 7/3.
Figure 3P.9.39
106. [latex]x=\frac{5}{4}[/latex]
107. [latex]y=-\frac{15}{4}[/latex]
Solution
The figure shows a straight horizontal line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The horizontal line goes through the points (0, negative 15/4), (1, negative 15/4), (2, negative 15/4) and all points with second coordinate negative 15/4.
Figure 3P.9.40
108. [latex]y=-\frac{5}{3}[/latex]

Exercises: Graph a Pair of Equations in the Same Rectangular Coordinate System

Instructions: For questions 109-112, graph each pair of equations in the same rectangular coordinate system.

109. [latex]y=2x[/latex] and [latex]y=2[/latex]
Solution
The figure shows a two straight lines drawn on the same x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. One line is a straight horizontal line going through the points (negative 4, 2) (0, 2), (4, 2), and all other points with second coordinate 2. The other line is a slanted line going through the points (negative 5, negative 10), (negative 4, negative 8), (negative 3, negative 6), (negative 2, negative 4), (negative 1, negative 2), (0, 0), (1, 2), (2, 4), (3, 6), (4, 8), and (5, 10).
Figure 3P.9.41
110. [latex]y=5x[/latex] and [latex]y=5[/latex]
111. [latex]y=-\frac{1}{2}x[/latex] and [latex]y=-\frac{1}{2}[/latex]
Solution
The figure shows a two straight lines drawn on the same x y-coordinate plane. The x-axis of the plane runs from negative 12 to 12. The y-axis of the plane runs from negative 12 to 12. One line is a straight horizontal line going through the points (negative 4, negative one half) (0, negative one half), (4, negative one half), and all other points with second coordinate negative one half. The other line is a slanted line going through the points (negative 10, 5), (negative 8, 4), (negative 6, 3), (negative 4, 2), (negative 2, 1), (0, 0), (1, negative 2), (2, negative 4), (3, negative 6), (4, negative 8), and (5, negative 10).
Figure 3P.9.42
112. [latex]y=-\frac{1}{3}x[/latex] and [latex]y=-\frac{1}{3}[/latex]

Exercises: Mixed Practice

Instructions: For questions 113-128, graph each equation.
113. [latex]y=4x[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 2, negative 8), (negative 1, negative 4), (0, 0), (1, 4), and (2, 8).
Figure 3P.9.43
114. [latex]y=2x[/latex]
115. [latex]y=-\frac{1}{2}x+3[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, 6), (negative 4, 5), (negative 2, 4), (0, 3), (2, 2), (4, 1), and (6, 0).
Figure 3P.9.44
116. [latex]y=\frac{1}{4}x-2[/latex]
117. [latex]y=-x[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, 6), (negative 5, 5), (negative 4, 4), (negative 3, 3), (negative 2, 2), (negative 1, 1), (0, 0), (1, negative 1), (2, negative 2), (3, negative 3), (4, negative 4), (5, negative 5), and (6, negative 6).
Figure 3P.9.45
118. [latex]y=x[/latex]
119. [latex]x-y=3[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 3, negative 7), (negative 2, negative 6), (negative 1, negative 4), (0, negative 3), (1, negative 2), (2, negative 1), (3, 0), (4, 1), (5, 2), and (6, 3).
Figure 3P.9.46
120. [latex]x+y=-5[/latex]
121. [latex]4x+y=2[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 2, 6), (negative 1, 4), (0, 2), (1, negative 2), and (2, negative 6).
Figure 3P.9.47
122. [latex]2x+y=6[/latex]
123. [latex]y=-1[/latex]
Solution
The figure shows a straight horizontal line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The horizontal line goes through the points (0, negative 1), (1, negative 1), (2, negative 1) and all points with second coordinate negative 1.
Figure 3P.9.48
124. [latex]y=5[/latex]
125. [latex]2x+6y=12[/latex]
Solution
The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The straight line goes through the points (negative 6, 4), (negative 3, 3), (0, 2), (3, 1), and (6, 0).
Figure 3P.9.49
126. [latex]5x+2y=10[/latex]
127. [latex]x=3[/latex]
Solution
The figure shows a straight vertical line drawn on the x y-coordinate plane. The x-axis of the plane runs from negative 7 to 7. The y-axis of the plane runs from negative 7 to 7. The vertical line goes through the points (3, 0), (3, 1), (3, 2) and all points with first coordinate 3.
Figure 3P.9.50
128. [latex]x=-4[/latex]

Exercises: Identify the [latex]\color{White} x[/latex] and [latex]\color{White} y[/latex]-Intercepts on a Graph

Instructions: For questions 129-140, find the [latex]x[/latex] and [latex]y[/latex]-intercepts on each graph.

129.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 5, 8), (negative 4, 7), (negative 3, 6), (negative 2, 5), (negative 1, 4), (0, 3), (1, 2), (2, 1), (3, 0), (4, negative 1), (5, negative 2) and (6, negative 3).
Figure 3P.9.51
Solution

[latex]\left(3,0\right),\left(0,3\right)[/latex]

130.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, 8), (negative 5, 7), (negative 4, 6), (negative 3, 5), (negative 2, 4), (negative 1, 3), (0, 2), (1, 1), (2, 0), (3, negative 1), (4, negative 2), (5, negative 3) and (6, negative 4).
Figure 3P.9.52

131.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 5, negative 10), (negative 4, negative 9), (negative 3, negative 8), (negative 2, negative 7), (negative 1, negative 6), (0, negative 5), (1, negative 4), (2, negative 3), (3, negative 2), (4, negative 1), (5, 0), (6, 1), (7, 2), and (8, 3).
Figure 3P.9.53
Solution

[latex]\left(5,0\right),\left(0,-5\right)[/latex]

132.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, negative 7), (negative 5, negative 6), (negative 4, negative 5), (negative 3, negative 4), (negative 2, negative 3), (negative 1, negative 2), (0, negative 1), (1, 0), (2, 1), (3, 2), (4, 3), (5, 4), (6, 5), (7, 6), and (8, 7).
Figure 3P.9.54

133.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, negative 7), (negative 5, negative 6), (negative 4, negative 5), (negative 3, negative 4), (negative 2, negative 3), (negative 1, negative 2), (0, negative 1), (1, 0), (2, 1), (3, 2), (4, 3), (5, 4), (6, 5), (7, 6), and (8, 7).
Figure 3P.9.55
Solution

[latex]\left(-2,0\right),\left(0,-2\right)[/latex]

134.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, 3), (negative 5, 2), (negative 4, 1), (negative 3, 0), (negative 2, negative 1), (negative 1, negative 2), (0, negative 3), (1, negative 4), (2, negative 5), (3, negative 6), (4, negative 7), (5, negative 8), and (6, negative 9).
Figure 3P.9.56

135.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, negative 5), (negative 5, negative 4), (negative 4, negative 3), (negative 3, negative 2), (negative 2, negative 1), (negative 1, 0), (0, 1), (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), and (8, 9).
Figure 3P.9.57
Solution

[latex]\left(-1,0\right),\left(0,1\right)[/latex]

136.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 8, negative 3), (negative 7, negative 2), (negative 6, negative 1), (negative 5, 0), (negative 4, 1), (negative 3, 2), (negative 2, 3), (negative 1, 4), (0, 5), (1, 6), (2, 7), (3, 8), (4, 9), and (5, 10).
Figure 3P.9.58

137.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 10, 8), (negative 8, 7), (negative 6, 6), (negative 4, 5), (negative 2, 4), (0, 3), (2, 2), (4, 1), (6, 0), (8, negative 1), and (10, negative 2).
Figure 3P.9.59
Solution

[latex]\left(6,0\right),\left(0,3\right)[/latex]

138.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. The straight line goes through the points (negative 6, 5), (negative 4, 4), (negative 2, 3), (0, 2), (2, 1), (4, 0), and (6, negative 1).
Figure 3P.9.60

139.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the plotted point (0, 0).
Figure 3P.9.61
Solution

[latex]\left(0,0\right)[/latex]

140.

The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. The straight line goes through the plotted point (0, 0).
Figure 3P.9.62

Exercises: Find the [latex]\color{White} x[/latex] and [latex]\color{White} y[/latex]-Intercepts from an Equation of a Line

Instructions: For questions 141-168, find the intercepts for each equation.

141. [latex]x+y=4[/latex]

Solution

[latex]\left(4,0\right),\left(0,4\right)[/latex]

142. [latex]x+y=3[/latex]
143. [latex]x+y=-2[/latex]
Solution

[latex]\left(-2,0\right),\left(0,-2\right)[/latex]

144. [latex]x+y=-5[/latex]
145. [latex]x–y=5[/latex]
Solution

[latex]\left(5,0\right),\left(0,-5\right)[/latex]

146. [latex]x–y=1[/latex]
147. [latex]x–y=-3[/latex]
Solution

[latex]\left(-3,0\right),\text{}\left(0,3\right)[/latex]

148. [latex]x–y=-4[/latex]
149. [latex]x+2y=8[/latex]
Solution

[latex]\left(8,0\right),\left(0,4\right)[/latex]

150. [latex]x+2y=10[/latex]
151. [latex]3x+y=6[/latex]
Solution

[latex]\left(2,0\right),\left(0,6\right)[/latex]

152. [latex]3x+y=9[/latex]
153. [latex]x–3y=12[/latex]
Solution

[latex]\left(12,0\right),\left(0,-4\right)[/latex]

154. [latex]x–2y=8[/latex]
155. [latex]4x–y=8[/latex]
Solution

[latex]\left(2,0\right),\left(0,-8\right)[/latex]

156. [latex]5x–y=5[/latex]
157. [latex]2x+5y=10[/latex]
Solution

[latex]\left(5,0\right),\left(0,2\right)[/latex]

158. [latex]2x+3y=6[/latex]
159. [latex]3x–2y=12[/latex]
Solution

[latex]\left(4,0\right),\left(0,-6\right)[/latex]

160. [latex]3x–5y=30[/latex]
161. [latex]y=\frac{1}{3}x+1[/latex]
Solution

[latex]\left(3,0\right),\left(0,1\right)[/latex]

162. [latex]y=\frac{1}{4}x-1[/latex]
163. [latex]y=\frac{1}{5}x+2[/latex]
Solution

[latex]\left(-10,0\right),\left(0,2\right)[/latex]

164. [latex]y=\frac{1}{3}x+4[/latex]
165. [latex]y=3x[/latex]
Solution

[latex]\left(0,0\right)[/latex]

166. [latex]y=-2x[/latex]
167. [latex]y=-4x[/latex]
Solution

[latex]\left(0,0\right)[/latex]

168. [latex]y=5x[/latex]

Exercises: Graph a Line Using the Intercepts

Instructions: For questions 169-194, graph using the intercepts.

169. [latex]–x+5y=10[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The line graphed is negative x plus 5 y equals 10.
Figure 3P.9.63
170. [latex]–x+4y=8[/latex]
171. [latex]x+2y=4[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 8, 6), (negative 6, 5), (negative 4, 4), (negative 2, 3), (0, 2), (2, 1), (4, 0), (6, negative 1), (8, negative 2), and (10, negative 3).
Figure 3P.9.64
172. [latex]x+2y=6[/latex]
173. [latex]x+y=2[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 8, 10), (negative 7, 9), (negative 6, 8),(negative 5, 7), (negative 4, 6), (negative 3, 5), (negative 2, 4), (negative 1, 3), (0, 2), (1, 1), (2, 0), (3, negative 1), (4, negative 2), (5, negative 3), (6, negative 4), (7, negative 5), (8, negative 6), (9, negative 7), and (10, negative 8).
Figure 3P.9.65
174. [latex]x+y=5[/latex]
175. [latex]x+y=-3[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. The straight line goes through the points (negative 7, 4), (negative 6, 3), (negative 5, 2),(negative 4, 1), (negative 3, 0), (negative 2, negative 1), (negative 1, negative 2), (0, negative 3), (1, negative 4), (2, negative 5), (3, negative 6), and (4, negative 7).
Figure 3P.9.66
176. [latex]x+y=-1[/latex]
177. [latex]x–y=1[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 8, negative 9), (negative 7, negative 8), (negative 6, negative 7),(negative 5, negative 6), (negative 4, negative 5), (negative 3, negative 4), (negative 2, negative 3), (negative 1, negative 2), (0, negative 1), (1, 0), (2, 1), (3, 2), (4, 3), (5, 4), (6, 5), (7, 6), (8, 7), (9, 8), and (10, 9).
Figure 3P.9.67
178. [latex]x–y=2[/latex]
179. [latex]x–y=-4[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 8, negative 4), (negative 7, negative 3), (negative 6, negative 2),(negative 5, negative 1), (negative 4, 0), (negative 3, 1), (negative 2, 2), (negative 1, 3), (0, 4), (1, 5), (2, 6), (3, 7), (4, 8), (5, 9), (6, 10), (7, 11), and (8, 12).
Figure 3P.9.68
180. [latex]x–y=-3[/latex]
181. [latex]4x+y=4[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 2, 12), (negative 1, 8), (0, 4), (1, 0), (2, negative 4), (3, negative 8), and (4, negative 12).
Figure 3P.9.69
182. [latex]3x+y=3[/latex]
183. [latex]2x+4y=12[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. The straight line goes through the points (negative 6, 6), (negative 4, 5), (negative 2, 4), (0, 3), (2, 2), (4, 1), and (6, 0).
Figure 3P.9.70
184. [latex]3x+2y=12[/latex]
185. [latex]3x–2y=6[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 6, negative 12), (negative 4, negative 9), (negative 2, negative 6), (0, negative 3), (2, 0), (4, 3), (6, 6), (8, 9), and (10, 12).
Figure 3P.9.71
186. [latex]5x–2y=10[/latex]
187. [latex]2x–5y=-20[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 10, 0), (negative 5, 2), (0, 4), (5, 6), and (10, 8).
Figure 3P.9.72
188. [latex]3x–4y=-12[/latex]
189. [latex]3x–y=-6[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 6, negative 12), (negative 5, negative 9), (negative 4, negative 6), (negative 3, negative 3), (negative 2, 0), (1, 3), (2, 6), (3, 9), and (4, 12).
Figure 3P.9.73
190. [latex]2x–y=-8[/latex]
191. [latex]y=-2x[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 5, 10), (negative 4, 8), (negative 3, 6), (negative 2, 4), (negative 1, 2), (0, 0), (1, negative 2), (2, negative 4), (3, negative 6), (4, negative 8), (5, negative 10), and (6, negative 12)
Figure 3P.9.74
192. [latex]y=-4x[/latex]
193. [latex]y=x[/latex]
Solution
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 10, 10), (negative 9, 9), (negative 8, 8), (negative 7, 7), (negative 6, 6), (negative 5, 5), (negative 4, 4), (negative 3, 3), (negative 2, 2), (negative 1, 1), (0, 0), (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (7, 7), (8, 8), (9, 9), and (10, 10)
Figure 3P.9.75
194. [latex]y=3x[/latex]

Exercises: Everyday Math

Instructions: For questions 195-200, answer the given everyday math word problems.

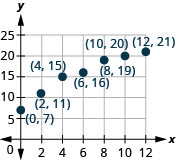
195. Weight of a baby. Mackenzie recorded her baby’s weight every two months. The baby’s age, in months, and weight, in pounds, are listed in the table below, and shown as an ordered pair in the third column.

a. Plot the points on a coordinate plane.

Coordinate plane with x-axis ranging from zero to twelve and y-axis ranging from zero to 25.
Figure 3P.9.76

b. Why is only Quadrant I needed?

Age [latex]x[/latex] Weight [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]0[/latex] [latex]7[/latex] [latex](0,7)[/latex]
[latex]2[/latex] [latex]11[/latex] [latex](2,11)[/latex]
[latex]4[/latex] [latex]15[/latex] [latex](4,15)[/latex]
[latex]6[/latex] [latex]16[/latex] [latex](6,16)[/latex]
[latex]8[/latex] [latex]19[/latex] [latex](8,19)[/latex]
[latex]10[/latex] [latex]20[/latex] [latex](10,20)[/latex]
[latex]12[/latex] [latex]21[/latex] [latex](12,21)[/latex]

 

Solution

a.

The graph shows the x y-coordinate plane. The x- and y-axes each run from 0 to 25. The points (0, 7), (2, 11), (4, 15), (6, 16), (8, 19), (10, 20) and (12, 21) are plotted and labeled.
Figure 3P.9.77

b. Age and weight are only positive.

196. Weight of a child. Latresha recorded her son’s height and weight every year. His height, in inches, and weight, in pounds, are listed in the table below, and shown as an ordered pair in the third column.

a. Plot the points on a coordinate plane.

A coordinate plane is displayed with an x-axis ranging from zero to fifty and a y-axis ranging from zero to 50.
Figure 3P.9.78

b. Why is only Quadrant I needed?

Height [latex]x[/latex] Weight [latex]y[/latex] [latex]\left(x,y\right)[/latex]
[latex]28[/latex] [latex]22[/latex] [latex](28,22)[/latex]
[latex]31[/latex] [latex]27[/latex] [latex](31,27)[/latex]
[latex]33[/latex] [latex]33[/latex] [latex](33,33)[/latex]
[latex]37[/latex] [latex]35[/latex] [latex](37,35)[/latex]
[latex]40[/latex] [latex]41[/latex] [latex](40,41)[/latex]
[latex]42[/latex] [latex]45[/latex] [latex](42,45)[/latex]
197. Motor home cost. The Robinsons rented a motor home for one week to go on vacation. It cost them [latex]$594[/latex] plus [latex]$0.32[/latex] per mile to rent the motor home, so the linear equation [latex]y=594+0.32x[/latex] gives the cost, [latex]y[/latex], for driving [latex]x[/latex] miles. Calculate the rental cost for driving [latex]400[/latex], [latex]800[/latex], and [latex]1200[/latex] miles, and then graph the line.
Solution

[latex]$722[/latex], [latex]$850[/latex], [latex]$978[/latex]

The figure shows a straight line drawn on the x y-coordinate plane. The x-axis of the plane runs from 0 to 1200 in increments of 100. The y-axis of the plane runs from 0 to 1000 in increments of 100. The straight line starts at the point (0, 594) and goes through the points (400, 722), (800, 850), and (1200, 978). The right end of the line has an arrow pointing up and to the right.
Figure 3P.9.79

198. Weekly earnings. At the art gallery where he works, Salvador gets paid [latex]$200[/latex] per week plus [latex]15\%[/latex] of the sales he makes, so the equation [latex]y=200+0.15x[/latex] gives the amount, [latex]y[/latex], he earns for selling [latex]x[/latex] dollars of artwork. Calculate the amount Salvador earns for selling [latex]$900[/latex], [latex]$1600[/latex], and [latex]$2000[/latex], and then graph the line.

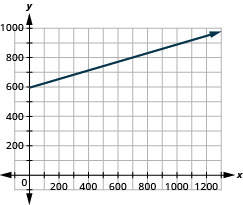
199. Road trip. Damien is driving from Chicago to Denver, a distance of [latex]1000 miles. The [latex]x[/latex]-axis on the graph below shows the time in hours since Damien left Chicago. The [latex]y[/latex]-axis represents the distance he has left to drive.

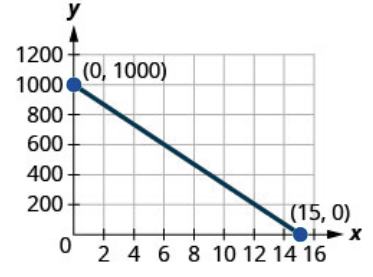
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from 0 to 16. The y- axis of the planes runs from 0 to 1200 in increments of 200. The straight line goes through the points (0, 1000), (3, 800), (6, 600), (9, 400), (12, 200), and (15, 0). The points (0, 1000) and (15, 0) are marked and labeled with their coordinates.
Figure 3P.9.80

a. Find the [latex]x[/latex] and [latex]y[/latex]-intercepts.
b. Explain what the [latex]x[/latex] and [latex]y[/latex]-intercepts mean for Damien.

Solution

a.[latex](0,1000),(15,0)[/latex]
b. At [latex](0,1000)[/latex], he has been gone [latex]0[/latex] hours and has [latex]1000[/latex] miles left. At [latex](15,0)[/latex], he has been gone [latex]15[/latex] hours and has [latex]0[/latex] miles left to go.

200. Road trip. Ozzie filled up the gas tank of his truck and headed out on a road trip. The [latex]x[/latex]-axis on the graph below shows the number of miles Ozzie drove since filling up. The [latex]y[/latex]-axis represents the number of gallons of gas in the truck’s gas tank.

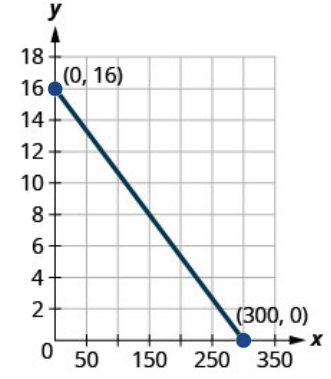
The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from 0 to 350 in increments of 50. The y- axis of the planes runs from 0 to 18 in increments of 2. The straight line goes through the points (0, 16), (150, 8), and (300, 0). The points (0, 16) and (300, 0) are marked and labeled with their coordinates
Figure 3P.9.81

a. Find the [latex]x[/latex] and [latex]y[/latex]-intercepts.
b. Explain what the [latex]x[/latex] and [latex]y[/latex]-intercepts mean for Ozzie.

Exercises: Writing Exercises

Instructions: For questions 201-210,
201. Explain in words how you plot the point [latex]\left(4,-2\right)[/latex] in a rectangular coordinate system.
Solution

Answers will vary.

202. How do you determine if an ordered pair is a solution to a given equation?
203. Is the point [latex]\left(-3,0\right)[/latex] on the [latex]x[/latex]-axis or [latex]y[/latex]-axis? How do you know?
Solution

Answers will vary.

204. Is the point [latex](0,8)[/latex] on the [latex]x[/latex]-axis or [latex]y[/latex]-axis? How do you know?

205. Explain how you would choose three [latex]x[/latex]-values to make a table to graph the line [latex]y=\frac{1}{5}x-2[/latex].

Solution

Answers will vary.

206. What is the difference between the equations of a vertical and a horizontal line?

207. How do you find the [latex]x[/latex]-intercept of the graph of [latex]3x–2y=6[/latex]?
Solution

Answers will vary.

208. Do you prefer to use the method of plotting points or the method using the intercepts to graph the equation [latex]4x+y=-4[/latex]? Why?
209. Do you prefer to use the method of plotting points or the method using the intercepts to graph the equation [latex]y=\frac{2}{3}x-2[/latex]? Why?
Solution

Answers will vary.

210. Do you prefer to use the method of plotting points or the method using the intercepts to graph the equation [latex]y=6[/latex]? Why?

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Fanshawe Pre-Health Sciences Mathematics 1 Copyright © 2022 by Domenic Spilotro, MSc is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book