Exercises: Accuracy, Precision, and Rounding Rules (2.2)
Exercises: Significant Figures and Proper Units
1. Suppose that your bathroom scale reads your mass as [latex]65[/latex] kg with a [latex]3\%[/latex] uncertainty. What is the uncertainty in your mass (in kilograms)?
Solution
[latex]2[/latex] kg
2. A good-quality measuring tape can be off by [latex]0.50[/latex] cm over a distance of [latex]20[/latex] m. What is its percent uncertainty?
3. A car speedometer has a [latex]5.0\%[/latex] uncertainty.
a. What is the range of possible speeds when it reads [latex]90[/latex] km/h?
b. Convert this range to miles per hour.
Solution
[latex](1\text{ km}=0.6214\text{ mi})[/latex]
a. [latex]85.5[/latex] to [latex]94.5[/latex] km/h
b. [latex]53.1[/latex] to [latex]58.7[/latex] mi/h
4. An infant’s pulse rate is measured to be [latex]130\pm5[/latex] beats/min. What is the percent uncertainty in this measurement?
5. Suppose that a person has an average heart rate of [latex]72.0[/latex] beats/min.
a. How many beats does he or she have in [latex]2.0[/latex] y?
b. In [latex]2.00[/latex] y?
c. In [latex]2.000[/latex] y?
Solution
a. [latex]7.6\times10^6[/latex] beats
b. [latex]7.57\times10^7[/latex] beats
c. [latex]7.57\times10^7[/latex] beats
6. A can contains [latex]375[/latex] mL of soda. How much is left after [latex]308[/latex] mL is removed?
7. State how many significant figures are proper in the results of the following calculations:
a. [latex](106.7)(98.2)/(46.210)(1.01)[/latex]
b. [latex](18.7)^2[/latex]
c. [latex](1.60\times10^{-19})(3712)[/latex]
Solution
a. [latex]3[/latex]
b. [latex]3[/latex]
c. [latex]3[/latex]
8.
a. How many significant figures are in the numbers [latex]99[/latex] and [latex]100[/latex]?
b. If the uncertainty in each number is [latex]1[/latex], what is the percent uncertainty in each?
c. Which is a more meaningful way to express the accuracy of these two numbers, significant figures or percent uncertainties?
9.
a. If your speedometer has an uncertainty of [latex]2.0[/latex] km/h at a speed of [latex]90[/latex] km/h, what is the percent uncertainty?
b. If it has the same percent uncertainty when it reads [latex]60[/latex] km/h, what is the range of speeds you could be going?
Solution
a. [latex]2.2\%[/latex]
b. [latex]59[/latex] to [latex]61[/latex] km/h
10.
a. A person’s blood pressure is measured to be [latex]120\pm2[/latex] mm Hg. What is its percent uncertainty?
b. Assuming the same percent uncertainty, what is the uncertainty in a blood pressure measurement of [latex]80[/latex] mm Hg?
11. A person measures his or her heart rate by counting the number of beats in [latex]30[/latex] s. If [latex]40\pm1[/latex] beats are counted in [latex]30.0\pm0.5[/latex] s, what is the heart rate and its uncertainty in beats per minute?
Solution
[latex]80\pm3\text{ beats/min}[/latex]
12. What is the area of a circle [latex]3.102[/latex] cm in diameter?
13. If a marathon runner averages [latex]9.5[/latex] mi/h, how long does it take him or her to run a [latex]26.22[/latex]-mi marathon?
Solution
[latex]2.8[/latex] h
14. A marathon runner completes a [latex]42.188[/latex]-km course in [latex]2[/latex] h, [latex]30[/latex] min, and [latex]12[/latex] s. There is an uncertainty of [latex]25[/latex] m in the distance travelled and an uncertainty of [latex]1[/latex] s in the elapsed time.
a. Calculate the percent uncertainty in the distance.
b. Calculate the uncertainty in the elapsed time.
c. What is the average speed in meters per second?
d. What is the uncertainty in the average speed?
15. The sides of a small rectangular box are measured to be [latex]1.80\pm0.01[/latex] cm, [latex]2.05\pm0.02[/latex] cm, and [latex]3.1\pm0.1[/latex] cm long. Calculate its volume and uncertainty in cubic centimetres.
Solution
[latex]11.4\pm0.5\text{ cm}^3[/latex]
16. When non-metric units were used in the United Kingdom, a unit of mass called the pound-mass (lbm) was employed, where [latex]1[/latex] lbm = [latex]0.4539[/latex] kg.
a. If there is an uncertainty of [latex]0.0001[/latex] kg in the pound-mass unit, what is its percent uncertainty?
b. Based on that percent uncertainty, what mass in pound-mass has an uncertainty of [latex]1[/latex] kg when converted to kilograms?
17. The length and width of a rectangular room are measured to be [latex]3.955\pm0.005[/latex] m and [latex]3.050\pm0.005[/latex] m. Calculate the area of the room and its uncertainty in square meters.
Solution
[latex]12.06\pm0.04\text{ m}^2[/latex]
18. A car engine moves a piston with a circular cross section of [latex]7.500\pm0.002[/latex] cm diameter a distance of [latex]3.250\pm0.001[/latex] cm to compress the gas in the cylinder.
a. By what amount is the gas decreased in volume in cubic centimetres?
b. Find the uncertainty in this volume.
Exercises: Significant Figures
19. Express each measurement to the correct number of significant figures.
a.

b.
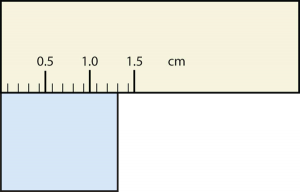
Solution
a. [latex]375[/latex] psi
b. [latex]1.30[/latex] cm
20. Express each measurement to the correct number of significant figures.
a.

b.
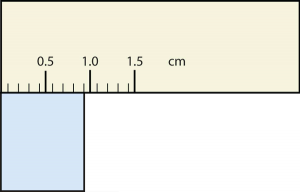
21. How many significant figures do these numbers have?
a. [latex]23[/latex]
b. [latex]23.0[/latex]
c. [latex]0.00023[/latex]
d. [latex]0.0002302[/latex]
Solution
a. Two
b. Three
c. Two
d. Four
22. How many significant figures do these numbers have?
a. [latex]5.44\times10^8[/latex]
b. [latex]1.008\times10^{-5}[/latex]
c. [latex]43.09[/latex]
d. [latex]0.0000001381[/latex]
23. How many significant figures do these numbers have?
a. [latex]765\text{,}890[/latex]
b. [latex]765\text{,}890.0[/latex]
c. [latex]1.2000\times10^5[/latex]
d. [latex]0.0005060[/latex]
Solution
a. Five
b. Seven
c. Five
d. Four
24. How many significant figures do these numbers have?
a. [latex]0.009[/latex]
b. [latex]0.0000009[/latex]
c. [latex]65\text{,}444[/latex]
d. [latex]65\text{,}040[/latex]
25. Compute and express each answer with the proper number of significant figures, rounding as necessary.
a. [latex]56.0+3.44=?[/latex]
b. [latex]0.00665+1.004=?[/latex]
c. [latex]45.99−32.8=?[/latex]
d. [latex]45.99−32.8+75.02=?[/latex]
Solution
a. [latex]59.4[/latex]
b. [latex]1.011[/latex]
c. [latex]13.2[/latex]
d. [latex]88.2[/latex]
26. Compute and express each answer with the proper number of significant figures, rounding as necessary.
a. [latex]1.005+17.88=?[/latex]
b. [latex]56,700−324=?[/latex]
c. [latex]405,007−123.3=?[/latex]
d. [latex]55.5+66.66−77.777=?[/latex]
27. Compute and express each answer with the proper number of significant figures, rounding as necessary.
a. [latex]56.7\times66.99=?[/latex]
b. [latex]1.000/77=?[/latex]
c. [latex]1.000/77.0=?[/latex]
d. [latex]6.022\times1.89=?[/latex]
Solution
a. [latex]3.80\times10^3[/latex]
b. [latex]0.013[/latex]
c. [latex]0.0130[/latex]
d. [latex]11.4[/latex]
28. Compute and express each answer with the proper number of significant figures, rounding as necessary.
a. [latex]0.000440\times17.22=?[/latex]
b. [latex]203\text{,}000/0.044=?[/latex]
c. [latex]67\times85.0\times0.0028=?[/latex]
d. [latex]999\text{,}999/3\text{,}310=?[/latex]
29. Write the number [latex]87\text{,}449[/latex] in scientific notation with four significant figures.
Solution
[latex]8.745\times10^4[/latex]
30. Write the number [latex]306\text{,}000\text{,}000[/latex] in scientific notation to the proper number of significant figures.
31. Write the number [latex]0.000066600[/latex] in scientific notation with five significant figures.
Solution
[latex]6.6600\times10^{-5}[/latex]
32. Write the number [latex]0.0000558[/latex] in scientific notation with two significant figures.
33. Perform each calculation and limit each answer to three significant figures.
a. [latex]67\text{,}883\times0.004321=?[/latex]
b. [latex](9.67\times10^3)\times0.0055087=?[/latex]
Solution
a. [latex]293[/latex]
b. [latex]53.3[/latex]
34. Perform each calculation and limit each answer to four significant figures.
a. [latex]18\text{,}900\times76.33/0.00336=?[/latex]
b. [latex]0.77604/76\text{,}003\times8.888=?[/latex]

