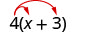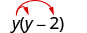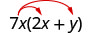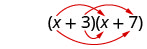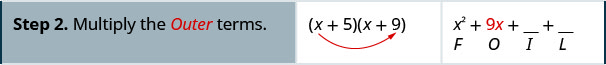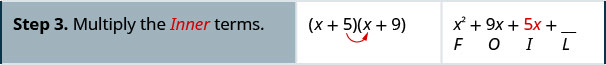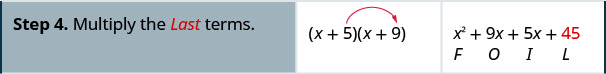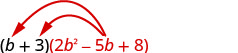5.3 Multiply Polynomials

Learning Objectives

By the end of this section, you will be able to:

  • Multiply a polynomial by a monomial
  • Multiply a binomial by a binomial
  • Multiply a trinomial by a binomial

Try it

Before you get started, take this readiness quiz:

1) Distribute: [latex]2(x+3)[/latex]
2) Combine like terms: [latex]{x}^{2}+9x+7x+63[/latex]

Multiply a Polynomial by a Monomial

We have used the Distributive Property to simplify expressions like [latex]2(x-3)[/latex]. You multiplied both terms in the parentheses, [latex]x[/latex] and [latex]3[/latex] by [latex]2[/latex], to get [latex]2x-6[/latex]. With this chapter’s new vocabulary, you can say you were multiplying a binomial, [latex]x-3[/latex], by a monomial, [latex]2[/latex].

Multiplying a binomial by a monomial is nothing new for you! Here’s an example:

Example 5.3.1

Multiply: [latex]4(x+3)[/latex]

Solution
4 times x plus 3. Two arrows extend from 4, terminating at x and 3.
Figure 5.3.1

Step 1: Distribute.

[latex]\begin{align*} &4\;\times\;x\;+\;4\;\times\;3\\ \text{Simplify.}\;\;&4x\;+\;12 \end{align*}[/latex]

Try It

3) Multiply: [latex]5(x+7)[/latex]

Solution

[latex]5x+35[/latex]

4) Multiply: [latex]3(y+13)[/latex]

Solution

[latex]3y+39[/latex]

Example 5.3.2

Multiply: [latex]y(y-2)[/latex]

Solution
y times y minus 2. Two arrows extend from the coefficient y, terminating at the y and minus 2 in parentheses.
Figure 5.3.2

Step 1: Distribute.

[latex]\begin{align*} &y\;\times\;y\;-\;y\;\times\;2\\ \text{Simplify.}\;\;&y^2\;-\;2y \end{align*}[/latex]

Try It

5) Multiply: [latex]x(x-7)[/latex]

Solution

[latex]{x}^{2}-7x[/latex]

6) Multiply: [latex]d(d-11)[/latex]

Solution

[latex]{d}^{2}-11d[/latex]

Example 5.3.3

Multiply: [latex]7x(2x+y)[/latex]

Solution
7 x times 2 x plus y. Two arrows extend from 7x, terminating at 2x and y.
Figure 5.3.3

Step 1: Distribute.

[latex]\begin{align*} &7x\;\times\;2x\;+\;7x\;\times\;y\\ \text{Simplify.}\;\;&14x^2\;+\;7xy \end{align*}[/latex]

Try It

7) Multiply: [latex]5x(x+4y)[/latex]

Solution

[latex]5{x}^{2}+20xy[/latex]

8) Multiply: [latex]2p(6p+r)[/latex]

Solution

[latex]12{p}^{2}+2pr[/latex]

Example 5.3.4

Multiply: [latex]-2y(4{y}^{2}+3y-5)[/latex]

Solution
Negative 2 y times 4 y squared plus 3 y minus 5. Three arrows extend from negative 2 y, terminating at 4 y squared, 3 y, and minus 5.
Figure 5.3.4

Step 1: Distribute.

[latex]\begin{align*} &-2y\;\times\;4y^2\;+\;(-2y)\;\times\;3y\;-\;(-2y)\;\times\;5\\ \text{Simplify.}\;\;&-8y^3\;-\;6y^2\;+\;10y \end{align*}[/latex]

Try It

9) Multiply: [latex]-3y(5{y}^{2}+8y-7)[/latex]

Solution

[latex]-15{y}^{3}-24{y}^{2}+21y[/latex]

10) Multiply: [latex]4{x}^{2}(2{x}^{2}-3x+5)[/latex]

Solution

[latex]8{x}^{4}-24{x}^{3}+20{x}^{2}[/latex]

Example 5.3.5

Multiply:  [latex]2{x}^{3}({x}^{2}-8x+1)[/latex]

Solution
2 x cubed times x squared minus 8 x plus 1. Three arrows extend from 2 x cubed, terminating at x squared, minus 8 x, and 1.
Figure 5.3.5

Step 1: Distribute.

[latex]\begin{align*} &2x^3\;\times\;x^2\;+\;(2x^3)\;\times\;(-8x)\;+\;(2x^3)\;\times\;1\\ \text{Simplify.}\;\;&2x^5\;-\;16x^4\;+\;2x^3 \end{align*}[/latex]

Try It

11) Multiply: [latex]4x(3{x}^{2}-5x+3)[/latex]

Solution

[latex]12{x}^{3}-20{x}^{2}+12x[/latex]

12) Multiply: [latex]-6{a}^{3}(3{a}^{2}-2a+6)[/latex]

Solution

[latex]-18{a}^{5}+12{a}^{4}-36{a}^{3}[/latex]

Example 5.3.6

Multiply: [latex](x+3)p[/latex].

Solution

Step 1: The monomial is the second factor.

x plus 3, in parentheses, times p. Two arrows extend from the p, terminating at x and 3.
Figure 5.3.6

Step 2: Distribute.

[latex]\begin{align*} &x\;\times\;p\;+\;3\;\times\;p\\ \text{Simplify.}\;\;&xp\;+\;3p \end{align*}[/latex]

Try It

13) Multiply: [latex](x+8)p[/latex]

Solution

[latex]xp+8p[/latex]

14) Multiply: [latex](a+4)p[/latex]

Solution

[latex]ap+4p[/latex]

Multiply a Binomial by a Binomial

Just like there are different ways to represent multiplication of numbers, there are several methods that can be used to multiply a binomial times a binomial. We will start by using the Distributive Property.

Multiply a Binomial by a Binomial Using the Distributive Property

Look at below table, where we multiplied a binomial by a monomial.

x plus 3, in parentheses, times p. Two arrows extend from the p, terminating at x and 3.
We distributed the [latex]p[/latex] to get: [latex]x{\color{red}{p}}+3{\color{red}{p}}[/latex]
What if we have [latex](x + 7)[/latex] instead of [latex]p[/latex]? x plus 3 multiplied by x plus 7. Two arrows extend from x plus 7, terminating at the x and the 3 in the first binomial.
Distribute [latex](x + 7)[/latex]. The sum of two products. The product of x and x plus 7, plus the product of 3 and x plus 7.
Distribute again. [latex]x^2+7x+3x+21[/latex]
Combine like terms. [latex]x^2+10x+21[/latex]

Notice that before combining like terms, you had four terms. You multiplied the two terms of the first binomial by the two terms of the second binomial—four multiplications.

Example 5.3.7

Multiply: [latex](y+5)(y+8)[/latex]

Solution
The product of two binomials, y plus 5 and y plus 8. Two arrows extend from y plus 8, terminating at the y and the 5 in the first binomial.
Figure 5.3.7

Step 1: Distribute [latex](y + 8)[/latex].

[latex]y{\color{red}{(y\;+\;8)}}\;+\;5{\color{red}{(y\;+\;8)}}[/latex]

Step 2: Distribute again

[latex]y^2\;+\;8y\;+\;5y\;+\;40[/latex]

Step 3: Combine like terms.

[latex]y^2\;+\;13y\;+\;40[/latex]

Try It

15) Multiply: [latex](x+8)(x+9)[/latex]

Solution

[latex]{x}^{2}+17x+72[/latex]

16) Multiply: [latex](5x+9)(4x+3)[/latex]

Solution

[latex]20{x}^{2}+51x+27[/latex]

Example 5.3.8

Multiply: [latex](2y+5)(3y+4)[/latex]

Solution
The product of two binomials, 2 y plus 5 and 3 y plus 4. Two arrows extend from 3y plus 4, terminating at 2y and 5 in the first binomial.
Figure 5.3.8

Step 1: Distribute [latex](3y + 4)[/latex].

[latex]{2y}\;{\color{red}{(3y\;+\;4)}}\;+\;5\;{\color{red}{(3y\;+\;4)}}[/latex]

Step 2: Distribute again

[latex]6y^2\;+\;8y\;+\;15y\;+\;20[/latex]

Step 3: Combine like terms.

[latex]6y^2\;+\;23y\;+\;20[/latex]

Try It

17) Multiply: [latex](3b+5)(4b+6)[/latex]

Solution

[latex]12{b}^{2}+38b+30[/latex]

18) Multiply: [latex](a+10)(a+7)[/latex]

Solution

[latex]{a}^{2}+17a+70[/latex]

Example 5.3.9

Multiply: [latex](4y+3)(2y-5)[/latex]

Solution

Step 1: Distribute.

[latex]4y\;{\color{red}{(2y\;-\;5)}}\;+\;3\;{\color{red}{(2y\;-\;5)}}[/latex]

Step 2: Distribute again.

[latex]8y^2\;-\;20y\;+\;6y\;-\;15[/latex]

Step 3: Combine like terms.

[latex]8y^2\;-\;14y\;-\;15[/latex]

Try It

19) Multiply: [latex](5y+2)(6y-3)[/latex]

Solution

[latex]30{y}^{2}-3y-6[/latex]

20) Multiply: [latex](3c+4)(5c-2)[/latex]

Solution

[latex]15{c}^{2}+14c-8[/latex]

Example 5.3.10

Multiply: [latex](x-2)(x-y)[/latex]

Solution
The product of two binomials, x minus 2 and x minus y. Two arrows extend from x minus y, terminating at x and 2 in the first binomial.
Figure 5.3.9

Step 1: Distribute.

[latex]{x}{\color{red}{(x\;-\;y)\;-}}\;2{\color{red}{(x\;-\;y)}}[/latex]

Step 2: Distribute again.

[latex]x^2\;-\;xy\;-\;2x\;+\;2y[/latex]

Step 3: There are no like terms to combine.

Try It

21) Multiply: [latex](a+7)(a-b)[/latex]

Solution

[latex]{a}^{2}-ab+7a-7b[/latex]

22) Multiply: [latex](x+5)(x-y)[/latex]

Solution

[latex]{x}^{2}-xy+5x-5y[/latex]

Multiply a Binomial by a Binomial Using the FOIL Method

Remember that when you multiply a binomial by a binomial you get four terms. Sometimes you can combine like terms to get a trinomial, but sometimes, like in the Example 5.3.10  there are no like terms to combine.

Let’s look at the last example again and pay particular attention to how we got the four terms.

[latex](x-2)(x-y)[/latex]
[latex]x^2 - xy -2x +2y[/latex]

Where did the first term, [latex]{x}^{2}[/latex], come from?

This figure explains how to multiply a binomial using the FOIL method. It has two columns, with written instructions on the left and math on the right. At the top of the figure, the text in the left column says “It is the product of x and x, the first terms in x minus 2 and x minus y.” In the right column is the product of x minus 2 and x minus y. An arrow extends from the x in x minus 2, and terminates at the x in x minus y. Below this is the word “First.” One row down, the text in the left column says “The next terms, negative xy, is the product of x and negative y, the two outer terms.” In the right column is the product of x minus 2 and x minus y, with another arrow extending from the x in x minus 2 to the y in x minus y. Below this is the word “Outer.” One row down, the text in the left column says “The third term, negative 2 x, is the product of negative 2 and x, the two inner terms.” In the right column is the product of x minus 2 and x minus y with a third arrow extending from minus 2 in x minus 2 and terminating at the x in x minus y. Below this is the word “Inner.” In the last row, the text in the left column says “And the last term, plus 2y, came from multiplying the two last terms, negative 2 and negative y.” In the right column is the product of x minus 2 and x minus y, with a fourth arrow extending from the minus 2 in x minus 2 to the minus y in x minus y. Below this is the word “Last.”
Figure 5.3.10

We abbreviate “First, Outer, Inner, Last” as FOIL. The letters stand for ‘First, Outer, Inner, Last’. The word FOIL is easy to remember and ensures we find all four products.

[latex](x-2)(x-y)[/latex]
[latex]x^2-xy-2x+2y[/latex]
F.   O.   I.    L

Let’s look at [latex](x+3)(x+7)[/latex].

Distributive Property FOIL
[latex](x+3)(x+7)[/latex]
The product of x plus 3 and x plus y. An arrow extends from the x in x plus 3 to the x in x plus 7. A second arrow extends from the x in x plus 3 to the 7 in x plus 7. A third arrow extends from the 3 in x plus 3 to the x in x plus 7. A fourth arrow extends from the 3 in x plus 3 to the 7 in x plus 7.
Figure 5.3.11
[latex]x(x+7)+3(x+7)[/latex]
[latex]\begin{array}{llllllll} &x^2&+&7x&+&3x&+&21&\\ &F&&O&&I&&L \end{array}[/latex] [latex]\begin{array}{llllllll} &x^2&+&7x&+&3x&+&21&\\ &F&&O&&I&&L \end{array}[/latex]
[latex]x^2+10x+21[/latex] [latex]x^2+10x+21[/latex]

Notice how the terms in third line fit the FOIL pattern.

Now we will do an example where we use the FOIL pattern to multiply two binomials.

Example 5.3.11

Multiply using the FOIL method: [latex](x+5)(x+9)[/latex]

Solution

 

This figure is a table that has three columns and five rows. The first column is a header column, and it contains the names and numbers of each step. The second and third columns contain math. On the top row of the table, the first cell on the left reads “Step 1: Multiply the first terms.” The second column contains the product of binomials x plus 5 and x plus 9. Below this is the product of x plus 5 and x plus 9 again, with an arrow extending from the x in the first binomial to the x in the second binomial. The third column contains x squared plus blank plus blank plus blank. Below the x squared is the letter F, and below each of the three blanks are the letters O, I, and L, respectively.
Figure 5.3.12
In the second row, the first cell reads “Step 2: Multiply the outer terms.” In the second cell is the product of x plus 5 and x plus 9 again, with an arrow extending from x in the first binomial to the 9 in the second binomial. The third cell contains x squared plus 9x plus blank plus blank, with the letter F under the x squared, O under the 9x, and I and L beneath the two blanks.
Figure 5.3.13
In the third row, the first cell reads “Step 3: Multiply the inner terms.” The second cell contains the product of x plus 5 and x plus 9 again, with an arrow extending from 5 in the first binomial to the x in the second binomial. The third cell contains x squared plus 9x plus 5x plus blank, with F beneath x squared, O beneath 9x, I beneath 5x, and L beneath the blank.
Figure 5.3.14
In the fourth row, the first cell reads “Step 4: Multiply the last terms.” In the second cell is the product of x plus 5 and x plus 9 again, with an arrow extending from 5 in the first binomial to 9 in the second binomial. The third cell contains x squared plus 9x plus 6x plus 45, with F beneath x squared, O beneath 9x, I beneath 6x, and L beneath 45.
Figure 5.3.15
In the final row, the first cell reads “Step 5: Combine like terms, when possible.” The second cell is blank. The third cell contains the final expression: x squared plus 15x plus 45.
Figure 5.3.16

Try It

23) Multiply using the FOIL method: [latex](x+6)(x+8)[/latex]

Solution

[latex]{x}^{2}+14x+48[/latex]

24) Multiply using the FOIL method: [latex](y+17)(y+3)[/latex]

Solution

[latex]{y}^{2}+20y+51[/latex]

We summarize the steps of the FOIL method below. The FOIL method only applies to multiplying binomials, not other polynomials!

Multiply two binomials using the FOIL method

HOW TO

Step 1: Mulitply the first terms. Step 2 Multiply the outer terms. Step 3: Multiply the inner terms. Step 4: Multiply the last terms. Step 5 Combine like terms when possible. Say it as you multiply! FOIL First Outer Inner Last
Figure 5.3.17

When you multiply by the FOIL method, drawing the lines will help your brain focus on the pattern and make it easier to apply.

Example 5.3.12

Multiply: [latex](y-7)(y+4)[/latex]

Solution
This figure has three columns, with written instructions in the first column and math in the second and third columns. At the top of the figure, the text in the first column says “Multiply the first terms.” The second column contains the product of two binomials, y minus 7 and y plus 4, with an arrow extending from the y in the first binomial to the y in the second binomial. The third column contains y squared plus blank plus blank plus blank. Beneath y squared is the letter F and beneath each blank are the letters O, I, and L, respectively. One row down, the text in the first column says “Multiply the outer terms.” The second column contains the product of y minus 7 and y plus 4 again, with a second arrow extending from y in the first binomial to 4 in the second binomial. The third column contains y squared plus 4y plus blank plus blank. Below y squared is F, below 4y is O, and below the blanks are I and L. One row down, the text in the first column says “Multiply the inner terms.” The middle column contains the product of y minus 7 and y plus 4 again, with a third arrow extending from the minus 7 in the first binomial to the y in the second binomial. The third column contains y squared plus 4y minus 7y plus blank. One row down, the text in the first column says “Multiply the last terms.” The second column contains the product of y minus 7 and y plus 4 again, with a fourth arrow extending from minus 7 in the first binomial to 4 in the second binomial. In the third column is the full expression, y squared plus 4y minus 7y minus 28, with each letter of FOIL beneath each of the terms. At the bottom of the image, the text in the first column says “Combine like terms.” In the right column is y squared minus 3y minus 28.
Figure 5.3.18

Try It

25) Multiply: [latex](x-7)(x+5)[/latex]

Solution

[latex]{x}^{2}-2x-35[/latex]

26) Multiply: [latex](b-3)(b+6)[/latex]

Solution

[latex]{b}^{2}+3b-18[/latex]

Example 5.3.13

Multiply: [latex](4x+3)(2x-5)[/latex]

Solution
This figure has three columns. At the top of the figure, the second column contains the product of two binomials, 4x plus 3 and 2x minus 5. One row down, the text in the first column says “Multiply the first terms. 4x times 2x.” The second column contains 8x squared plus blank plus blank plus blank. Beneath 8x squared is the letter F and beneath each blank are the letters O, I, and L, respectively. One row down, the text in the first column says “Multiply the outer terms. 4x times negative 5.” The second column contains 8x squared minus 20x plus blank plus blank. Below 8x squared is F, below 20x is O, and below the blanks are I and L. One row down, the text in the first column says “Multiply the inner terms. 3 times 2x.” The second column contains 8x squared minus 20x plus 6x plus blank. One row down, the text in the first column says “Multiply the last terms. 3 times negative 5.” The second column contains the full expression, 8x squared minus 20x plus 6x minus 15, with each letter of FOIL beneath each of the terms. At the bottom of the image, the text in the first column says “Combine like terms.” In the right column is 8x squared minus 14x minus 15. In the third column is the product of the two binomials again, 4x plus 3 times 2x minus 5. An arrow extends from 4x in the first binomial to 2x in the second binomial. A second arrow extends from 4x in the first binomial to minus 5 in the second binomial. A third arrow extends from 3 in the first binomial to 2x in the second binomial. A fourth arrow extends from 3 in the first binomial to minus 5 in the second binomial.
Figure 5.3.19

Try It

27) Multiply: [latex](3x+7)(5x-2)[/latex]

Solution

[latex]15{x}^{2}+29x-14[/latex]

28) Multiply: [latex](4y+5)(4y-10)[/latex]

Solution

[latex]16{y}^{2}-20y-50[/latex]

The final products in the last four examples were trinomials because we could combine the two middle terms. This is not always the case.

Example 5.3.14

Multiply: [latex](3x-y)(2x-5)[/latex]

Solution
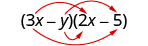
An arrow extends from 3 x in the first binomial to 2 x in the second binomial. A second arrow extends from 3 x in the first binomial to minus 5 in the second binomial. A third arrow extends from y in the first binomial to 2 x in the second binomial. A fourth arrow extends from y in the first binomial to minus 5 in the second binomial.
Figure 5.3.20

Step 1: Multiply the First.

[latex]\underset{F}{\color{red}{6x^2}}\;+\;\underset{O}{\_\_}\;+\;\underset{I}{\_\_}\;+\;\underset{L}{\;\_\_}[/latex]

Step 2: Multiply the Outer.

[latex]\underset{F}{\color{red}{6x^2}}\;{\color{red}{-}}\;\underset{O}{\color{red}{15x}}\;+\;\underset{I}{\_\_}\;+\;\underset{L}{\;\_\_}[/latex]

Step 3: Multiply the Inner.

[latex]\underset{F}{6x^2}\;-\;\underset{O}{15x}\;{\color{red}{-}}\;\underset{I}{\color{red}{2xy}}\;+\;\underset{L}{\;\_\_}[/latex]

Step 4: Multiply the Last.

[latex]\underset{F}{6x^2}\;-\;\underset{O}{15x}\;-\;\underset{I}{2xy}\;{\color{red}{+}}\;\underset{L}{\color{red}{5y}}[/latex]

Step 5: Combine like terms—there are none.

[latex]6x^2\;-\;15x\;-\;2xy\;+\;5y[/latex]

Try It

29) Multiply: [latex](10c-d)(c-6)[/latex]

Solution

[latex]10{c}^{2}-60c-cd+6d[/latex]

30) Multiply: [latex](7x-y)(2x-5)[/latex]

Solution

[latex]14{x}^{2}-35x-2xy+10y[/latex]

Be careful of the exponents in the next example.

Example 5.3.15

Multiply: [latex]({n}^{2}+4)(n-1)[/latex]

Solution
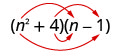
The product of two binomials, n squared plus 4 and n minus 1. An arrow extends from n squared in the first binomial to n in the second binomial. A second arrow extends from n squared in the first binomial to minus 1 in the second binomial. A third arrow extends from 4 in the first binomial to n in the second binomial. A fourth arrow extends from 4 in the first binomial to minus 1 in the second binomial.
Figure 5.3.21

Step 1: Multiply the First.

[latex]\underset{F}{\color{red}{n^3}}\;+\;\underset{O}{\_\_}\;+\;\underset{I}{\_\_}\;+\;\underset{L}{\;\_\_}[/latex]

Step 2: Multiply the Outer.

[latex]\underset{F}{n^3}\;{\color{red}{-}}\;\underset{O}{\color{red}{n^2}}\;+\;\underset{I}{\_\_}\;+\;\underset{L}{\;\_\_}[/latex]

Step 3: Multiply the Inner.

[latex]\underset{F}{n^3}\;-\;\underset{O}{n^2}\;{\color{red}{+}}\;\underset{I}{\color{red}{4n}}\;+\;\underset{L}{\;\_\_}[/latex]

Step 4: Multiply the Last.

[latex]\underset{F}{n^3}\;-\;\underset{O}{n^2}\;+\;\underset{I}{4n}\;{\color{red}{-}}\;\underset{L}{\color{red}{4}}[/latex]

Step 5: Combine like terms—there are none.

[latex]n^3\;-\;n^2\;+\;4n\;-\;4[/latex]

Try It

31) Multiply: [latex]({x}^{2}+6)(x-8)[/latex]

Solution

[latex]{x}^{3}-8{x}^{2}+6x-48[/latex]

32) Multiply: [latex]({y}^{2}+7)(y-9)[/latex]

Solution

[latex]{y}^{3}-9{y}^{2}+7y-63[/latex]

Example 5.3.16

Multiply: [latex](3pq+5)(6pq-11)[/latex]

Solution
(3pq+5)(6pq-11). Arrows from: 3pq to 6pq; 3pq to 11; 5 to 6pq; 5 to 11
Figure 5.3.22

Step 1: Multiply the First.

[latex]\underset F{\color{red}{18p^2q^2}}\;+\;\underset O{\_\_}\;+\;\underset I{\_\_}\;+\;\underset L{\_\_}[/latex]

Step 2: Multiply the Outer.

[latex]\underset F{18p^2q^2}\;{\color{red}{-}}\;\underset{O}{\color{red}{33pq}}\;+\;\underset I{\_\_}\;+\;\underset L{\_\_}[/latex]

Step 3: Multiply the Inner.

[latex]\underset F{18p^2q^2}\;-\;\underset O{33pq}\;{\color{red}{+}}\;\underset{I}{\color{red}{30pq}}\;+\;\underset L{\_\_}[/latex]

Step 4: Multiply the Last.

[latex]\underset F{18p^2q^2}\;-\;\underset O{33pq}\;+\;\underset I{30pq}\;{\color{red}{-}}\;{\color{red}{\underbrace{55}_{\color{black}{L}}}}[/latex]

Step 5: Combine like terms—there are none.

[latex]18p^2q^2\;-\;3pq\;-\;55\;[/latex]

Try It

33) Multiply: [latex](2ab+5)(4ab-4)[/latex]

Solution

[latex]8{a}^{2}{b}^{2}+12ab-20[/latex]

34) Multiply: [latex](2xy+3)(4xy-5)[/latex]

Solution

[latex]8{x}^{2}{y}^{2}+2xy-15[/latex]

Multiply a Binomial by a Binomial Using the Vertical Method

The FOIL method is usually the quickest method for multiplying two binomials, but it only works for binomials. You can use the Distributive Property to find the product of any two polynomials. Another method that works for all polynomials is the Vertical Method. It is very much like the method you use to multiply whole numbers. Look carefully at this example of multiplying two-digit numbers.

[latex]\begin{alignat*}{3} &\;\;\;23\\ &\underline{\times46}\;\\ &\;\;138\;&&\;\text{partial product}\;\;\;\;\;&&\text{Start by multiplying 23 by 6 to get 138.}\\ &\underline{\;\;92\;\;}&&\;\text{partial product}\;\;\;\;\;&&\text{Next, multiply 23 by 4, lining up the partial product in the correct columns.}\\ &1058\;&&\;\text{product}\;\;\;\;\;&&\text{Last you add the partial products.} \end{alignat*}[/latex]

Now we’ll apply this same method to multiply two binomials.

Example 5.3.17

Multiply using the Vertical Method: [latex](3y-1)(2y-6)[/latex]

Solution

It does not matter which binomial goes on the top.

Step 1: Multiply [latex]3y -1[/latex] by [latex]-6[/latex]

Step 2: Multiply [latex]3y-1[/latex] by [latex]2y[/latex]

Step 3: Add like terms.

Notice the partial products are the same as the terms in the FOIL method.

[latex]\begin{align*}(3y-1)(2y-6)\\{\color{blue}{\underline{6y2^2-2y}}}{\color{red}{\underline{\;-18y+6}}}\\6y^2-20y+6\end{align*}[/latex] [latex]\begin{align*}3y-1\\\underline{\times2y-6}\\{\color{red}{-18y+6}}\\{\color{blue}{6y^2-2y}}\;\;\;\;\;\;\;\\\overline{6y^2-20x+6}\end{align*}[/latex]

Try It

35) Multiply using the Vertical Method: [latex](5m-7)(3m-6)[/latex]

Solution

[latex]15{m}^{2}-51m+42[/latex]

36) Multiply using the Vertical Method: [latex](6b-5)(7b-3)[/latex]

Solution

[latex]42{b}^{2}-53b+15[/latex]

We have now used three methods for multiplying binomials. Be sure to practice each method, and try to decide which one you prefer. The methods are listed here all together, to help you remember them.

Multiplying Two Binomials

HOW TO

To multiply binomials, use the:

  • Distributive Property
  • FOIL Method
  • Vertical Method

Remember, FOIL only works when multiplying two binomials.

Multiply a Trinomial by a Binomial

We have multiplied monomials by monomials, monomials by polynomials, and binomials by binomials. Now we’re ready to multiply a trinomial by a binomial. Remember, FOIL will not work in this case, but we can use either the Distributive Property or the Vertical Method. We first look at an example using the Distributive Property.

Example 5.3.18

Multiply using the Distributive Property: [latex](b+3)(2{b}^{2}-5b+8)[/latex]

Solution
The product of a binomial, b plus 3, and a trinomial, 2 b squared minus 5 b plus 8. Two arrows extend from the trinomial, terminating at b and 3 in the binomial.
Figure 5.3.23

Step 1: Distribute.

The sum of two products, the product of b and 2 b squared minus 5 b plus 8, and the product of 3 and 2 b squared minus 5 b plus 8.
Figure 5.3.24

Step 2: Multiply.

[latex]2b^3\;-\;5b^2\;+\;8b\;+\;6b^2\;-\;15b\;+\;24[/latex]

Step 3: Combine like terms.

[latex]2b^3\;+\;b^2\;-\;7b\;+\;24[/latex]

Try It

37) Multiply using the Distributive Property: [latex](y-3)({y}^{2}-5y+2)[/latex]

Solution

[latex]{y}^{3}-8{y}^{2}+17y-6[/latex]

38) Multiply using the Distributive Property: [latex](x+4)(2{x}^{2}-3x+5)[/latex]

Solution

[latex]2{x}^{3}+5{x}^{2}-7x+20[/latex]

Now let’s do this same multiplication using the Vertical Method.

Example 5.3.19

Multiply using the Vertical Method: [latex](b+3)(2{b}^{2}-5b+8)[/latex]

Solution

Step 1: Multiply [latex](2b^2-5b+8)[/latex] by [latex]3[/latex].

[latex]\begin{align*} 2b^2-5b+8&\\ \times\;\;\;\;\;\;\;b+3&\\ \overline{6b^2-15b+24}& \end{align*}[/latex]

Step 2: Multiply [latex](2b^2-5b+8)[/latex] by [latex]b[/latex].

[latex]2b^3\;-\;5b^2\;+\;8b[/latex]

Step 3: Add like terms.

[latex]2b^3\;+\;b^2\;-\;7b\;+\;24[/latex]

It is easier to put the polynomial with fewer terms on the bottom because we get fewer partial products this way.

Try It

39) Multiply using the Vertical Method: [latex](y-3)({y}^{2}-5y+2)[/latex]

Solution

[latex]{y}^{3}-8{y}^{2}+17y-6[/latex]

40) Multiply using the Vertical Method: [latex](x+4)(2x^2-3x+5)[/latex]

Solution

[latex]2x^3+5x^2-7x+20[/latex]

We have now seen two methods you can use to multiply a trinomial by a binomial. After you practice each method, you’ll probably find you prefer one way over the other. We list both methods are listed here, for easy reference.

Multiplying a Trinomial by a Binomial

HOW TO

To multiply a trinomial by a binomial, use the:

  • Distributive Property
  • Vertical Method

Access these online resources for additional instruction and practice with multiplying polynomials:

Key Concepts

  • FOIL Method for Multiplying Two Binomials—To multiply two binomials:
    1. Multiply the First terms.
    2. Multiply the Outer terms.
    3. Multiply the Inner terms.
    4. Multiply the Last terms.
  • Multiplying Two Binomials—To multiply binomials, use the:
    • Distributive Property (Example 5.3.7)
    • FOIL Method (Example 5.3.11)
    • Vertical Method (Example 5.3.17)

  • Multiplying a Trinomial by a Binomial—To multiply a trinomial by a binomial, use the:
    • Distributive Property (Example 5.3.18)
    • Vertical Method (Example 5.3.19)

Self Check

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

What does this checklist tell you about your mastery of this section? What steps will you take to improve?

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Fanshawe Pre-Health Sciences Mathematics 1 Copyright © 2022 by Domenic Spilotro, MSc is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book