1.1 Introduction to Whole Numbers
Learning Objectives
By the end of this section, you will be able to:
- Use place value with whole numbers
- Identify multiples and apply divisibility tests
- Find prime factorizations and least common multiples
As we begin our study of elementary algebra, we need to refresh some of our skills and vocabulary. This chapter will focus on whole numbers, integers, fractions, decimals, and real numbers. We will also begin our use of algebraic notation and vocabulary.
Use Place Value with Whole Numbers
The most basic numbers used in algebra are the numbers we use to count objects in our world: 1, 2, 3, 4, and so on. These are called the counting numbers. Counting numbers are also called natural numbers. If we add zero to the counting numbers, we get the set of whole numbers.
Counting Numbers: 1, 2, 3, …
Whole Numbers: 0, 1, 2, 3, …
The notation “…” is called ellipsis and means “and so on,” or that the pattern continues endlessly.
[latex]\\\xleftarrow{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;smaller\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\\overleftrightarrow{o\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overset{\xrightarrow[{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Larger\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}]{}}{3\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;4\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;5\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;6}\;\;\;\;\;\;\;\;\;\;}[/latex]
The numbers on the number line get larger as they go from left to right and smaller as they go from right to left. While this number line shows only the whole numbers 0 through 6, the numbers keep going without end.
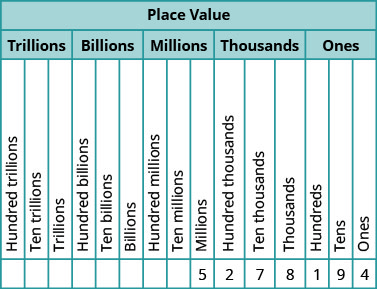
Our number system is called a place value system, because the value of a digit depends on its position in a number. Figure 1.1 shows the place values. The place values are separated into groups of three, which are called periods. The periods are ones, thousands, millions, billions, trillions, and so on. In a written number, commas separate the periods.
Example 1.1.1
In the number 63,407,218, find the place value of each digit:
- 7
- 0
- 1
- 6
- 3
Solution
Place the number in the place value chart:
- The 7 is in the thousands place.
- The 0 is in the ten-thousands place.
- The 1 is in the tens place.
- The 6 is in the ten-millions place.
- The 3 is in the millions place.
Try It
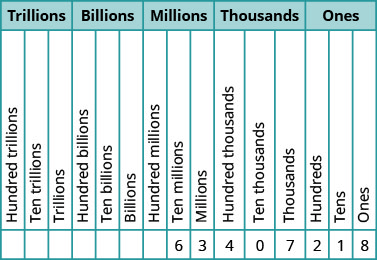
1) For the number 27,493,615, find the place value of each digit:
- 2
- 1
- 4
- 7
- 5
Solution
- ten millions
- tens
- hundred thousands
- millions
- ones
2) For the number 519,711,641,328, find the place value of each digit:
- 9
- 4
- 2
- 6
- 7
Solution
- billions
- ten thousands
- tens
- hundred thousands
- hundred millions
When you write a check, you write out the number in words as well as in digits. To write a number in words, write the number in each period, followed by the name of the period, without the s at the end. Start at the left, where the periods have the largest value. The ones period is not named. The commas separate the periods, so wherever there is a comma in the number, put a comma between the words (see below). The number 74,218,369 is written as seventy-four million, two hundred eighteen thousand, three hundred sixty-nine.
HOW TO
Name a Whole Number in Words
- Start at the left and name the number in each period, followed by the period name.
- Put commas in the number to separate the periods.
- Do not name the ones period
Example 1.1.2
Name the number 8,165,432,098,710 using words.
Solution
Step 1: Name the number in each period, followed by the period name.
[latex]\underbrace{\;\;\;\;8\;\;\;\;}_{trillions}\;,\underbrace{\;\;\;\;\;\;\;\;165\;\;\;\;\;\;}_{billions}\;,\underbrace{\;\;\;\;\;\;\;\;\;432\;\;\;\;\;\;\;}_{millions},\;\underbrace{\;\;\;\;\;\;098\;\;\;\;\;\;}_{thousands},\;\underbrace{\;\;\;\;\;\;710\;\;\;\;\;}_{ones}\;\;\;\\8\xrightarrow[{}]{}Eight\;trillion,\\165\xrightarrow[{}]{}One\;hundred\;sixty-five\;billion,\\432\xrightarrow[{}]{}Four\;hundred\;thrity-two\;million,\;\\098\xrightarrow[{}]{}Ninety-eight\;thousand,\\710\xrightarrow[{}]{}seven\;hundred\;ten[/latex]
Step 2: Put the commas in to separate the periods.
So, 8,165,432,098,710 is named as eight trillion, one hundred sixty-five billion, four hundred thirty-two million, ninety-eight thousand, seven hundred ten.
Try It
3) Name the number 9,258,137,904,061 using words.
Solution
Nine trillion, two hundred fifty-eight billion, one hundred thirty-seven million, nine hundred four thousand, sixty-one.
4) Name the number 17,864,325,619,004 using words.
Solution
Seventeen trillion, eight hundred sixty-four billion, three hundred twenty-five million, six hundred nineteen thousand four.
We are now going to reverse the process by writing the digits from the name of the number. To write the number in digits, we first look for the clue words that indicate the periods. It is helpful to draw three blanks for the needed periods and then fill in the blanks with the numbers, separating the periods with commas.
HOW TO
Write a Whole Number Using Digits
-
- Identify the words that indicate periods. (Remember, the ones period is never named.)
- Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.
- Name the number in each period and place the digits in the correct place value position.
Example 1.1.3
Write nine billion, two hundred forty-six million, seventy-three thousand, one hundred eighty-nine as a whole number using digits.
Solution
Step 1: Identify the words that indicate periods.
Except for the first period, all other periods must have three places. Draw three blanks to indicate the number of places needed in each period.
Step 2: Separate the periods by commas.
Then write the digits in each period.
[latex]\underbrace{\;\;\;\;\;billions\;\;\;\;\;}_{nine\;billion}\;,\underbrace{\;\;\;\;\;\;\;\;\;\;\;millions\;\;\;\;\;\;\;\;\;\;}_{two\;hundred\;forty-six\;million}\;,\underbrace{\;\;\;\;\;\;\;\;\;\;thousands\;\;\;\;\;\;\;\;\;}_{seventy-three\;thousand},\;\underbrace{\;\;\;\;\;\;\;\;\;\;\;\;ones\;\;\;\;\;\;\;\;\;\;}_{one\;hundred\;eity-nine},\;\\\;\;\;\;\;\;\;\;\;\\\begin{array}{ccc}\;\;\;\;&&\end{array}9\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;246\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;073\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;189\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;[/latex]
The number is 9,246,073,189.
Try It
5) Write the number two billion, four hundred sixty-six million, seven hundred fourteen thousand, fifty-one as a whole number using digits.
Solution
2,466,714,051
6) Write the number eleven billion, nine hundred twenty-one million, eight hundred thirty thousand, one hundred six as a whole number using digits.
Solution
11,921,830,106
The process of approximating a number is called rounding. Numbers are rounded to a specific place value, depending on how much accuracy is needed. Saying that the population of New York is approximately 20 million means that we rounded to the millions place.
Example 1.1.4
Round 23,658 to the nearest hundred.
Solution
Step 1: Locate the given place value with an arrow. All digits to the left do not change.
Locate the hundreds place 23,658.
[latex]{\color{red}{\text{Hundredths}}}\text{ place.}\;23,{\color{red}{\underset\uparrow6}}{58}[/latex]
Step 2: Underline the digit to the right of the given place value.
Underline the 5, which is to the right of the hundreds place.
[latex]{\color{red}{\text{Hundredths}}}\text{ place.}\;23,{\color{red}{6}}{\color{blue}{\underline5}}{8}[/latex]
Step 3: Is this digit greater than or equal to 5?
Yes – add 1 to the digit in the given place value.
Add 1 to the 6 in the hundred place, since 5 is greater than or equal to 5.
[latex]{\text{Add 1.}\;23,}{\color{red}{6}}{\color{black}{5}}{8}[/latex]
Step 4: Replace all digits to the right of the given place with zeros.
Replace all digits to the right of the hundreds place with zeros.
[latex]{\text{Replace with zeros.}\;23,}{\color{blue}{700}}[/latex]
Try It
7) Round to the nearest hundred: 17,852.
Solution
17,900
8) Round to the nearest hundred: 468,751.
Solution
468,800
Round Whole Numbers.
- Locate the given place value and mark it with an arrow. All digits to the left of the arrow do not change.
- Underline the digit to the right of the given place value.
- Is this digit greater than or equal to 5?
- Yes–add 1 to the digit in the given place value.
- No–do not change the digit in the given place value.
- Replace all digits to the right of the given place value with zeros.
Examples 1.1.5
Round 103,978 to the nearest:
- hundred
- thousand
- ten thousand
Solution
a.
Step 1: Locate the hundreds place in 103,978.
[latex]{\color{red}{\text{Hundreds place:}}}{\;103,\boxed{\color{red}{9}}}{78}[/latex]
Step 2: Underline the digit to the right of the hundreds place.
[latex]{\color{red}{\text{Hundreds place:}}}{\;103,\boxed{\color{red}{9}}}{\underline78}[/latex]
Step 3: Since 7 is greater than or equal to 5, add 1 to the 9. Replace all digits to the right of the hundreds place with zeros.
[latex]{\color{red}{\text{Hundreds place:}}}{\;103,\boxed{\underbrace{\color{red}{9}}{_{Add\;1\;\;\\9+1=10\\replace\;9\;with\;0\\and\;carry\;the\;1}}}\underbrace{\underline78}_{\;replace\;with\;0s\\}=\;104,000}[/latex]
So, 104,000 is 103,978 rounded to the nearest hundred.
b.
Step 1: Locate the thousands place and underline the digit to the right of the thousands place.
[latex]{\color{red}{\text{Thousands place:}}}{\;10\;\boxed{\color{red}{3}}}{,\underline978}[/latex]
Step 2: Since 9 is greater than or equal to 5, add 1 to the 3. Replace all digits to the right of the hundreds place with zeros.
[latex]{\color{red}{\text{Thousands place:}}}{\;10\;\boxed{\underbrace{\color{red}{3}}{_{Add\;1\;\;\\3+1=4\\replace\;3\;with\;4}}}\underbrace{\underline978}_{\;replace\;with\;0s\\}=\;104,000}[/latex]
So, 104,000 is 103,978 rounded to the nearest thousand.
c.
Step 1: Locate the ten thousands place and underline the digit to the right of the ten thousands place.
[latex]{\color{red}{\text{Ten thousands place:}}}{\;1\boxed{\color{red}{0}}}{3,978}[/latex]
Step 2: Since 3 is less than 5, we leave the 0 as is, and then replace the digits to the right with zeros.
[latex]100,000[/latex]
So, 100,000 is 103,978 rounded to the nearest ten thousand.
Try It
9) Round 206,981 to the nearest:
- hundred
- thousand
- ten thousand.
Solution
- 207,000
- 207,000
- 210,000
10) Round 784,951 to the nearest:
- hundred
- thousand
- ten thousand.
Solution
- 785,000
- 785,000
- 780,000
Identify Multiples and Apply Divisibility Tests
The numbers 2, 4, 6, 8, 10, and 12 are called multiples of 2. A multiple of 2 can be written as the product of a counting number and 2.
| 2 | 2 · 1 |
| 4 | 2 · 2 |
| 6 | 2 · 3 |
| 8 | 2 · 4 |
| 10 | 2 · 5 |
| 12 | 2 · 6 |
Similarly, a multiple of 3 would be the product of a counting number and 3.
| 3 | 3 · 1 |
| 6 | 3 · 2 |
| 9 | 3 · 3 |
| 12 | 3 · 4 |
| 15 | 3 · 5 |
| 18 | 3 · 6 |
We could find the multiples of any number by continuing this process.
Table. 1.1 shows the multiples of 2 through 9 for the first 12 counting numbers.
| Counting Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Multiples of 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| Multiples of 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| Multiples of 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| Multiples of 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Multiples of 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| Multiples of 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| Multiples of 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| Multiples of 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| Multiples of 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
Multiple of a Number
A number is a multiple of [latex]n[/latex] if it is the product of a counting number and [latex]n[/latex].
Another way to say that 15 is a multiple of 3 is to say that 15 is divisible by 3. That means that when we divide 3 into 15, we get a counting number. In fact, [latex]15\div3[/latex] is [latex]5[/latex], so [latex]15[/latex] is [latex]15\times3[/latex].
Divisible by a Number
If a number [latex]m[/latex] is a multiple of [latex]n[/latex], then [latex]m[/latex] is divisible by [latex]n[/latex].
Look at the multiples of 5 in Table 1.1. They all end in 5 or 0. Numbers with last digit of 5 or 0 are divisible by 5. Looking for other patterns in Table 1.1 that shows multiples of the numbers 2 through 9, we can discover the following divisibility tests:
Divisibility Tests
A number is divisible by:
- 2 if the last digit is 0, 2, 4, 6, or 8.
- 3 if the sum of the digits is divisible by 3.
- 4 if the last two digits are divisible by 4.
- 5 if the last digit is 5 or 0.
- 6 if it is divisible by both 2 and 3.
- 8 if it is divisible by 2 and 4.
- 9 if the sum of the digits is divisible by 9.
- 10 if it ends with 0.
Example 1.1.6
Is 5,625 divisible by 2? By 3? By 5? By 6? By 10?
Solution
Step 1: Is 5,625 divisible by 2?
No.
Step 2: Does it end in 0,2,4,6, or 8?
5,625 is not divisible by 2.
Step 3: Is 5,625 divisible by 3?
Yes. 5,625 is divisible by 3.
Step 4: What is the sum of the digits?
[latex]5+6+2+5=18[/latex]
Step 5: Is the sum divisible by 3?
Yes, 18 is divisible by 3.
Step 6: Is 5,625 divisible by 5 or 10?
5,625 is divisible by 5 but not by 10.
Step 7: What is the last digit?
It is 5.
Step 8: Is 5,625 divisible by 6?
No, it is not.
Step 9: Is it divisible by both 2 or 3?
No, 5,625 is not divisible by 2, but it is divisible by 3.
Try It
11) Determine whether 4,962 is divisible by 2, by 3, by 5, by 6, and by 10.
Solution
By 2, 3, and 6.
12) Determine whether 3,765 is divisible by 2, by 3, by 5, by 6, and by 10.
Solution
By 3 and 5.
Find Prime Factorizations and Least Common Multiples
In mathematics, there are often several ways to talk about the same ideas. So far, we’ve seen that if [latex]m[/latex] is a multiple of [latex]n[/latex], we can say that [latex]m[/latex] is divisible by [latex]n[/latex]. For example, since 72 is a multiple of 8, we say 72 is divisible by 8. Since 72 is a multiple of 9, we say 72 is divisible by 9. We can express this still another way.
Since [latex]8\times9=72[/latex], we say that 8 and 9 are factors of 72. When we write [latex]72=8\times9[/latex], we say we have factored 72.
[latex]\underbrace{8\times9}_{factors}=\underbrace{72}_{product}[/latex]
Other ways to factor 72 are 1·72, 2·36, 3·24, 4·18, and 6·12. Seventy-two has many factors: 1, 2, 3, 4, 6, 8, 9, 12, 18, 36, and 72.
Factors
If [latex]a\cdot b=m[/latex] then [latex]a[/latex] and [latex]b[/latex] are factors of [latex]m[/latex].
Some numbers, like 72, have many factors. Other numbers have only two factors.
A prime number is a counting number greater than 1, whose only factors are 1 and itself.
A composite number is a counting number that is not prime. A composite number has factors other than 1 and itself.
The counting numbers from 2 to 19 are listed in the below table, with their factors. Make sure to agree with the “prime” or “composite” label for each!
| Number | Factors | Prime or Composite |
|---|---|---|
| 2 | 1,2 | Prime |
| 3 | 1,3 | Prime |
| 4 | 1,2,4 | Composite |
| 5 | 1,5 | Prime |
| 6 | 1,2,3,6 | Composite |
| 7 | 1,7 | Prime |
| 8 | 1,2,4,8 | Composite |
| 9 | 1,3,9 | Composite |
| 10 | 1,2,5,10 | Composite |
| 11 | 1,11 | Prime |
| 12 | 1,2,3,4,6,12 | Composite |
| 13 | 1,13 | Prime |
| 14 | 1,2,7,14 | Composite |
| 15 | 1,3,5,15 | Composite |
| 16 | 1,2,4,8,16 | Composite |
| 17 | 1,17 | Prime |
| 18 | 1,2,3,6,9,18 | Composite |
| 19 | 1,19 | Prime |
The prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, and 19. Notice that the only even prime number is 2.
A composite number can be written as a unique product of primes. This is called the prime factorization of the number. Finding the prime factorization of a composite number will be useful later in this course.
Prime Factorization
The prime factorization of a number is the product of prime numbers that equals the number. These prime numbers are called the prime factors.
To find the prime factorization of a composite number, find any two factors of the number and use them to create two branches. If a factor is prime, that branch is complete. Circle that prime!
If the factor is not prime, find two factors of the number and continue the process. Once all the branches have circled primes at the end, the factorization is complete. The composite number can now be written as a product of prime numbers.
Example 1.1.7
Factor 48.
Solution
4 and 8 are not prime. Break them each into two factors.
2 and 3 are prime, so circle them.
Step 1: Find two factors whose product is the given number. Use these numbers to create two branches.
[latex]48=2\times24\;\;\;\;\;\;\;\;\;\;\overbrace{2\;\;\;\;\;\;\;\;\;24}^{48}[/latex]
Step 2: If a factor is prime, that branch is complete. Circle the prime.
2 is prime. Circle the prime.
[latex]\overbrace{\boxed2\;\;\;\;\;\;\;\;\;\;\;\;\;\;24}^{48}[/latex]
Step 3: If a factor is not prime, write it as the product of two factors and continue the process.
24 is not prime break it into 2 more factors.4 and 6 are not prime. Break them each into two factors.
[latex]\overbrace{\boxed2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\overbrace{4\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;6}^{24}}^{48}[/latex]
2 and 3 are prime, so circle them.
[latex]\overbrace{\boxed2\;\;\;\;\;\;\;\;\overbrace{\overbrace{\boxed2\;\;\;\;\;\;\;\;\boxed2}^4\;\;\;\;\;\;\;\;\;\;\;\;\overbrace{\boxed2\;\;\;\;\;\;\;\;\;\boxed3}^6}^{24}}^{48}[/latex]
Step 4: Write the composite number as the product of all the circled primes.
[latex]48=2\times2\times2\times2\times3[/latex]
We say 2·2·2·2·3 is the prime factorization of 48. We generally write the primes in ascending order. Be sure to multiply the factors to verify your answer!
If we first factored 48 in a different way, for example as 6·8, the result would still be the same. Finish the prime factorization and verify this for yourself.
Try It
13) Find the prime factorization of 80.
Solution
2·2·2·2·5
14) Find the prime factorization of 60.
Solution
2·2·3·5
Find the Prime Factorization of a Composite Number.
- Find two factors whose product is the given number, and use these numbers to create two branches.
- If a factor is prime, that branch is complete. Circle the prime, like a bud on the tree.
- If a factor is not prime, write it as the product of two factors and continue the process.
- Write the composite number as the product of all the circled primes.
Example 1.1.8
Find the prime factorization of 252.
Solution
Step 1: Find two factors whose product is 252. 12 and 21 are not prime.
Break 12 and 21 into two more factors. Continue until all primes are factored.
[latex]252\left\{\begin{array}{l}12\left\{\begin{array}{l}6\left\{\begin{array}{l}3\\2\end{array}\right.\\2\end{array}\right.\\21\left\{\begin{array}{l}3\\7\end{array}\right.\end{array}\right.[/latex]
Step 2: Write 252 as the product of all the circled primes.
[latex]252=2·2·3·3·7[/latex]
Try It
15) Find the prime factorization of 126.
Solution
2·3·3·7
16) Find the prime factorization of 294.
Solution
2·3·7·7
One of the reasons we look at multiples and primes is to use these techniques to find the least common multiple of two numbers. This will be useful when we add and subtract fractions with different denominators. Two methods are used most often to find the least common multiple and we will look at both of them.
The first method is the Listing Multiples Method. To find the least common multiple of 12 and 18, we list the first few multiples of 12 and 18:
12: 12, 24, 36, 48, 60, 72, 84, 96, 108…
18: 18, 36, 54, 72, 90, 108…
Common Multiples: 36, 72, 108…
Least Common Multiple: 36
Notice that some numbers appear in both lists. They are the common multiples of 12 and 18.
We see that the first few common multiples of 12 and 18 are 36, 72, and 108. Since 36 is the smallest of the common multiples, we call it the least common multiple. We often use the abbreviation LCM.
Least Common Multiple
The least common multiple (LCM) of two numbers is the smallest number that is a multiple of both numbers.
The procedure box lists the steps to take to find the LCM using the prime factors method we used above for 12 and 18.
HOW TO
Find the Least Common Multiple by Listing Multiples.
- List several multiples of each number.
- Look for the smallest number that appears on both lists.
- This number is the LCM.
Example 1.1.9
Find the least common multiple of 15 and 20 by listing multiples.
Solution
Step 1: Make lists of the first few multiples of 15 and of 20, and use them to find the least common multiple.
15: 15, 30, 45, 60, 75, 90, 105, 120
20: 20, 40, 60, 80, 100, 120, 140, 160
Step 2: Look for the smallest number that appears in both lists.
The first number to appear on both lists is 60, so 60 is the least common multiple of 15 and 20.
Notice that 120 is in both lists, too. It is a common multiple, but it is not the least common multiple.
Try It
17) Find the least common multiple by listing multiples: 9 and 12.
Solution
36
18) Find the least common multiple by listing multiples: 18 and 24.
Solution
72
Our second method to find the least common multiple of two numbers is to use The Prime Factors Method. Let’s find the LCM of 12 and 18 again, this time using their prime factors.
Example 1.1.10
Find the Least Common Multiple (LCM) of 12 and 18 using the prime factors method.
Solution
Step 1: Write each number as a product of primes.
[latex]\overbrace{\boxed3\;\;\;\;\;\;\;\;\;\overbrace{\boxed2\;\;\;\;\;\;\boxed{\;3}}^6}^{18}[/latex]
[latex]\overbrace{\boxed3\;\;\;\;\;\;\;\;\;\overbrace{\boxed2\;\;\;\;\;\;\boxed{\;2}}^4}^{12}[/latex]
Step 2: List the primes of each number. Match primes vertically when possible.
List the primes of 12.
[latex]12=2\times2\times3[/latex]
List the primes of 18. Line up with the primes of 12 when possible. If not create a new column.
[latex]18=2\times3\times3[/latex]
Step 3: Bring down the number from each column.
[latex]\begin{eqnarray*}12&=&2\times2\times3\\18&=&2\times\hspace{0.94cm}3\times3\\LCM&=&2\times2\times3\times3\end{eqnarray*}[/latex]
Step 4: Multiply the factors.
[latex]LCM=36[/latex]
Notice that the prime factors of 12 (2·2·3) and the prime factors of 18 (2·3·3) are included in the LCM (2·2·3·3). So 36 is the least common multiple of 12 and 18.
By matching up the common primes, each common prime factor is used only once. This way you are sure that 36 is the least common multiple.
Try It
19) Find the LCM using the prime factors method: 9 and 12.
Solution
36
20) Find the LCM using the prime factors method: 18 and 24.
Solution
72
HOW TO
Find the Least Common Multiple Using the Prime Factors Method.
- Write each number as a product of primes.
- List the primes of each number. Match primes vertically when possible.
- Bring down the columns.
- Multiply the factors.
Example 1.1.11
Find the Least Common Multiple (LCM) of 24 and 36 using the prime factors method.
Solution
Step 1: Find the primes of 24 and 36.
Match primes vertically when possible.
Step 2: Bring down all columns.
[latex]\begin{eqnarray*}24&=&2\times2\times2\times3\\36&=&2\times2\hspace{0.94cm}\times3\times3\end{eqnarray*}[/latex]
Step 3: Multiply the factors.
[latex]\begin{eqnarray*}LCM&=&2\times2\times2\times3\times3\\LCM&=&72\end{eqnarray*}[/latex]
The LCM of 24 and 36 is 72.
Try It
21) Find the LCM using the prime factors method: 21 and 28.
Solution
84
22) Find the LCM using the prime factors method: 24 and 32.
Solution
96
Key Concepts
- Place Value
- Name a Whole Number in Words
- Start at the left and name the number in each period, followed by the period name.
- Put commas in the number to separate the periods.
- Do not name the ones period.
- Write a Whole Number Using Digits
- Identify the words that indicate periods. (Remember the ones period is never named.)
- Draw 3 blanks to indicate the number of places needed in each period. Separate the periods by commas.
- Name the number in each period and place the digits in the correct place value position.
- Round Whole Numbers
- Locate the given place value and mark it with an arrow. All digits to the left of the arrow do not change.
- Underline the digit to the right of the given place value.
- Is this digit greater than or equal to 5?
- Yes—add 1 to the digit in the given place value.
- No—do not change the digit in the given place value.
- Replace all digits to the right of the given place value with zeros.
- Divisibility Tests: A number is divisible by:
- 2 if the last digit is 0, 2, 4, 6, or 8.
- 3 if the sum of the digits is divisible by 3.
- 5 if the last digit is 5 or 0.
- 6 if it is divisible by both 2 and 3.
- 10 if it ends with 0.
- Find the Prime Factorization of a Composite Number
- Find two factors whose product is the given number, and use these numbers to create two branches.
- If a factor is prime, that branch is complete. Circle the prime, like a bud on the tree.
- If a factor is not prime, write it as the product of two factors and continue the process.
- Write the composite number as the product of all the circled primes.
- Find the Least Common Multiple by Listing Multiples
- List several multiples of each number.
- Look for the smallest number that appears on both lists.
- This number is the LCM.
- Find the Least Common Multiple Using the Prime Factors Method
- Write each number as a product of primes.
- List the primes of each number. Match primes vertically when possible.
- Bring down the columns.
- Multiply the factors.
Self Check
After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Glossary
- composite number
- A composite number is a counting number that is not prime. A composite number has factors other than 1 and itself.
- counting numbers
- The counting numbers are the numbers 1, 2, 3, …
- divisible by a number
- If a number [latex]m[/latex] is a multiple of [latex]n[/latex], then [latex]m[/latex] is divisible by [latex]n[/latex]. (If 6 is a multiple of 3, then 6 is divisible by 3.)
- factors
- If [latex]a\;\times\;b\;=\;m[/latex], then ([latex]a[/latex] and [latex]b[/latex]) are factors of [latex]m[/latex]. Since [latex]3 \times 4 = 12[/latex], then 3 and 4 are factors of 12.
- least common multiple
- The least common multiple of two numbers is the smallest number that is a multiple of both numbers.
- multiple of a number
- A number is a multiple of [latex]n[/latex] if it is the product of a counting number and [latex]n[/latex].
- number line
- A number line is used to visualize numbers. The numbers on the number line get larger as they go from left to right, and smaller as they go from right to left.
- origin
- The origin is the point labelled 0 on a number line.
- prime factorization
- The prime factorization of a number is the product of prime numbers that equals the number.
- prime number
- A prime number is a counting number greater than 1, whose only factors are 1 and itself.
- whole numbers
- The whole numbers are the numbers 0, 1, 2, 3, ….
The counting numbers are the numbers 1, 2, 3, …
A number line is used to visualize numbers. The numbers on the number line get larger as they go from left to right, and smaller as they go from right to left.
If [latex]a\timesb=m[/latex], then (a and b) are factors of m.
A prime number is a counting number greater than 1, whose only factors are 1 and itself.
A composite number is a counting number that is not prime. A composite number has factors other than 1 and itself.
The prime factorization of a number is the product of prime numbers that equals the number.
The least common multiple of two numbers is the smallest number that is a multiple of both numbers
If a number m is a multiple of n, then m is divisible by n.
A number is a multiple of n if it is the product of a counting number and n.
The origin is the point labeled 0 on a number line.
The whole numbers are the numbers 0, 1, 2, 3, ....
