Rate of return of a financial portfolio

L. El Ghaoui

Rate of return of a financial portfolio

Rate of return of a single asset

The rate of return $r$ (or, return) of a financial asset over a given period (say, a year, or a day) is the interest obtained at the end of the period by investing in it. In other words, if, at the beginning of the period, we invest a sum 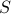in the asset, we will earn $S_{end} := (1+r)S$ at the end. That is:

$r = \dfrac{S_{end}-S}{S}.$

Log-returns

Often, the rates of return are approximated, especially if the period length is small. If $r \ll 1$ , then

$r = \dfrac{S_{end}}{S}-1 \thickapprox y := \log \dfrac{S_{end}}{S},$

with the latter quantity known as log-return.

Rate of return of a portfolio

For $n$ assets, we can define the vector $r \in \mathbb{R}^{n}$ , with $r_{i}$ the rate of return of the $i$ -th asset.

Assume that at the beginning of the period, we invest a sum $S$ in all the assets, allocating a fraction $x_{i}$ (in %) in the $i$ -th asset. Here $x \in \mathbb{R}^{n}$ is a non-negative vector which sums to one. Then the portfolio we constituted this way will earn

$S_{end} := \sum_{i=1}^{n}(1+r+{i})x_{i}S.$

The rate of return of the porfolio is the relative increase in wealth:

$\dfrac{S_{end}-S}{S} = \sum_{i=1}^{n}(1+r+{i})x_{i}-1=\sum_{i=1}^{n}x_{i} - 1 + \sum_{i=1}^{n}r_{i}x_{i} = r^{T}x.$

The rate of return is thus the scalar product between the vector of individual returns $r$ and of the portfolio allocation weights $x$ .

Note that, in practice, rates of return are never known in advance, and they can be negative (although, by construction, they are never less than $-1$ ).

Rate of return of a financial portfolio

Rate of return of a single asset

Log-returns

Rate of return of a portfolio

License

Share This Book