Matrix Products
- Matrix-vector product
- Matrix-matrix product
- Block matrix product
- Trace and scalar product
Matrix-vector product
Definition
We define the matrix-vector product between a ![]() matrix and a
matrix and a ![]() -vector
-vector ![]() , and denote by
, and denote by ![]() , the
, the ![]() -vector with
-vector with ![]() -th component
-th component
![Rendered by QuickLaTeX.com \[(Ax)_{i}=\sum_{j=1}^{n}A_{ij}x_{j}, i=1,\dots,m.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-39196c108ce8b8f1d44932dd842c69bf_l3.png)
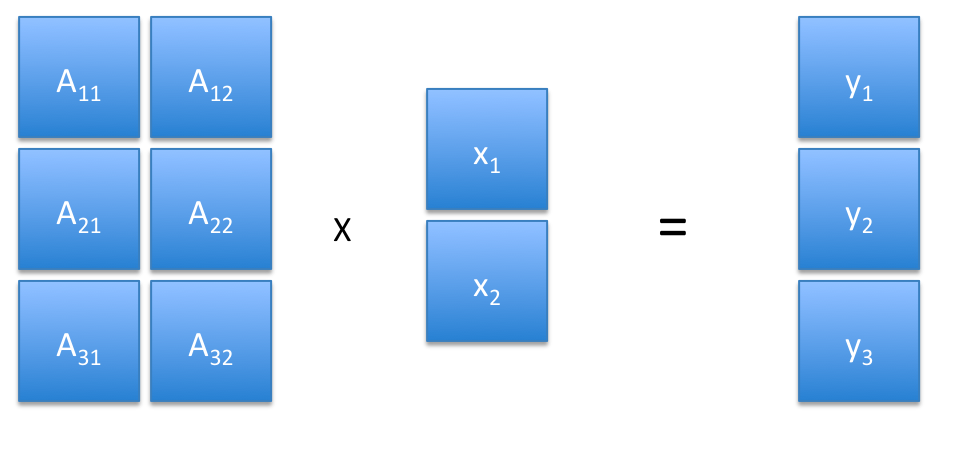 |
The picture on the left shows a symbolic example with |
Interpretation as linear combinations of columns
If the columns of ![]() are given by the vectors
are given by the vectors ![]() so that
so that ![]() , then
, then ![]() can be interpreted as a linear combination of these columns, with weights given by the vector
can be interpreted as a linear combination of these columns, with weights given by the vector ![]() :
:
![]()
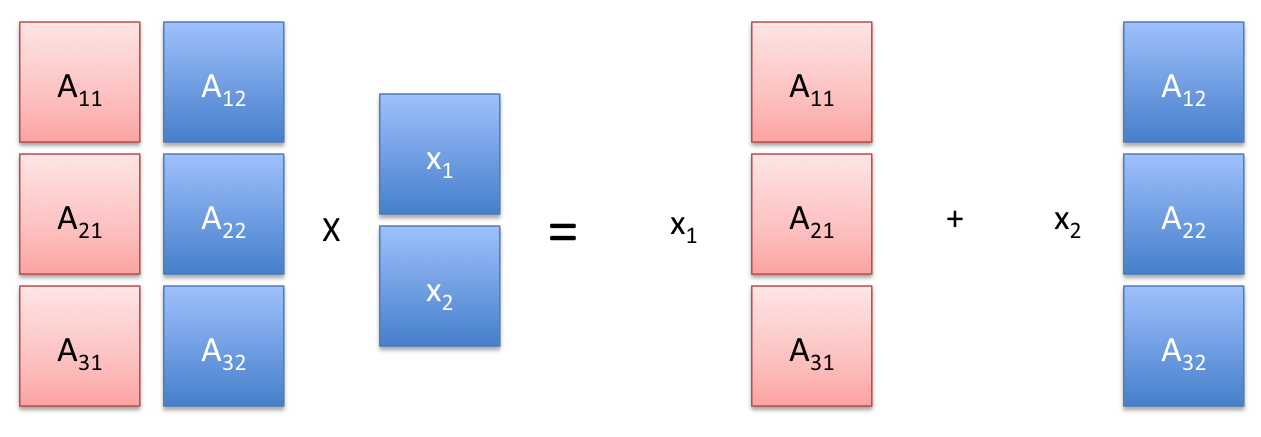 |
In the above symbolic example, we have |
Example:
Interpretation as scalar products with rows
Alternatively, if the rows of ![]() are the row vectors
are the row vectors ![]() :
:
![Rendered by QuickLaTeX.com \[A = \begin{pmatrix} a_{1}^{T} \\ \vdots \\ a_{m}^{T} \end{pmatrix},\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-cfbe8fa25c3e32d95b5f44ab358b383f_l3.png)
then ![]() is the vector with elements
is the vector with elements ![]() :
:
![Rendered by QuickLaTeX.com \[Ax = \begin{pmatrix} a_{1}^{T}x \\ \vdots \\ a_{m}^{T}x \end{pmatrix}.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0d54b8e614e79aebb4a94e32476d318b_l3.png)
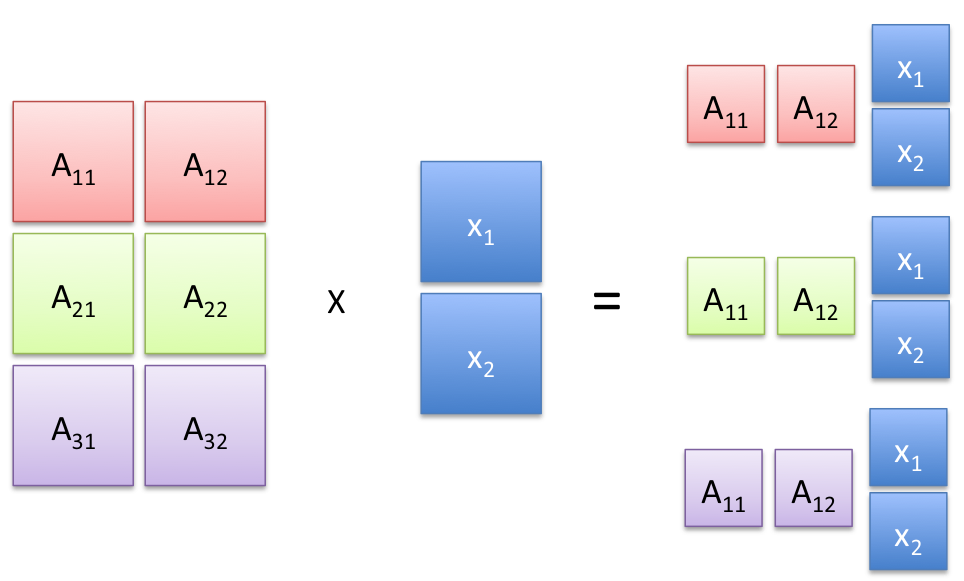 |
In the above symbolic example, we have |
Example: Absorption spectrometry: using measurements at different light frequencies.
Left product
If ![]() , then the notation
, then the notation ![]() is the row vector of size
is the row vector of size ![]() equal to the transpose of the column vector
equal to the transpose of the column vector ![]() . That is:
. That is:
![]()
Example: Return to the network example, involving a ![]() incidence matrix. We note that, by construction, the columns of
incidence matrix. We note that, by construction, the columns of ![]() sum to zero, which can be compactly written as
sum to zero, which can be compactly written as ![]() , or
, or ![]() .
.
Matlab syntax
The product operator in Matlab is *. If the sizes are not consistent, Matlab will produce an error.
>> A = [1 2; 3 4; 5 6]; % 3x2 matrix >> x = [-1; 1]; % 2x1 vector >> y = A*x; % result is a 3x1 vector >> z = [-1; 0; 1]; % 3x1 vector >> y = z'*A; % result is a 1x2 (i.e., row) vector
Matrix-matrix product
Definition
We can extend the matrix-vector product to the matrix-matrix product, as follows. If ![]() and
and ![]() , the notation
, the notation ![]() denotes the
denotes the ![]() matrix with
matrix with ![]() element given by
element given by
![Rendered by QuickLaTeX.com \[(AB)_{ij} = \sum_{k=1}^{n}A_{ik}B_{kj}.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5f2c7d1df13e109c04ace92b5a7168f8_l3.png)
Transposing a product changes the order, so that ![]()
Column-wise interpretation
If the columns of ![]() are given by the vectors
are given by the vectors ![]() so that
so that ![]() then
then ![]() can be written as
can be written as
![]()
In other words, ![]() results from transforming each column
results from transforming each column ![]() of
of ![]() into
into ![]() .
.
Row-wise interpretation
The matrix-matrix product can also be interpreted as an operation on the rows of ![]() . Indeed, if
. Indeed, if ![]() is given by its rows
is given by its rows ![]() then
then ![]() is the matrix obtained by transforming each one of these rows via
is the matrix obtained by transforming each one of these rows via ![]() , into
, into ![]() :
:
![Rendered by QuickLaTeX.com \[AB = \begin{pmatrix}a_{1}^{T} \\ \vdots \\ a_{n}^{T}\end{pmatrix}B= \begin{pmatrix}a_{1}^{T}B \\ \vdots \\ a_{n}^{T}B\end{pmatrix}.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8f09c33085519bf23b916f1e289bb1f9_l3.png)
(Note that ![]() ‘s are indeed row vectors, according to our matrix-vector rules.)
‘s are indeed row vectors, according to our matrix-vector rules.)
Block Matrix Products
Matrix algebra generalizes to blocks, provided block sizes are consistent. To illustrate this, consider the matrix-vector product between a ![]() matrix
matrix ![]() and a
and a ![]() -vector
-vector ![]() , where
, where ![]() are partitioned in blocks, as follows:
are partitioned in blocks, as follows:
![]()
where ![]() is
is ![]() Then
Then ![]()
Symbolically, it’s as if we would form the ‘‘scalar’’ product between the ‘‘row vector ![]() and the column vector
and the column vector ![]() !
!
Likewise, if a ![]() matrix
matrix ![]() is partitioned into two blocks
is partitioned into two blocks ![]() , each of size
, each of size ![]() , with
, with ![]() , then
, then
![]()
Again, symbolically we apply the same rules as for the scalar product — except that now the result is a matrix.
Example: Gram matrix.
Finally, we can consider so-called outer products. Consider the case for example when ![]() is a
is a ![]() matrix partitioned row-wise into two blocks
matrix partitioned row-wise into two blocks ![]() , and
, and ![]() is a
is a ![]() matrix that is partitioned column-wise into two blocks
matrix that is partitioned column-wise into two blocks ![]() :
:
![]()
Then the product ![]() can be expressed in terms of the blocks, as follows:
can be expressed in terms of the blocks, as follows:
![]()
Trace, scalar product
Trace
The trace of a square ![]() matrix
matrix ![]() , denoted by
, denoted by ![]() , is the sum of its diagonal elements:
, is the sum of its diagonal elements: ![]() .
.
Some important properties:
- Trace of transpose: The trace of a square matrix is equal to that of its transpose.
- Commutativity under trace: for any two matrices
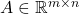 and
and 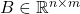 , we have
, we have
![]()
>> A = [1 2 3; 4 5 6; 7 8 9]; % 3x3 matrix >> tr = trace(A); % trace of A
Scalar product between matrices
We can define the scalar product between two ![]() matrices
matrices ![]() via
via
![Rendered by QuickLaTeX.com \[\langle A,B \rangle = Tr(A^{T}B) = \sum_{i=1}^{m}\sum_{j=1}^{m}A_{ij}B_{ij}.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-7b6708f016a7091c939f4dd77eaf8040_l3.png)
The above definition is symmetric: we have
![]()
Our notation is consistent with the definition of the scalar product between two vectors, where we simply view a vector in ![]() as a matrix in
as a matrix in ![]() . We can interpret the matrix scalar product as the vector scalar product between two long vectors of length
. We can interpret the matrix scalar product as the vector scalar product between two long vectors of length ![]() each, obtained by stacking all the columns of
each, obtained by stacking all the columns of ![]() on top of each other.
on top of each other.
>> A = [1 2; 3 4; 5 6]; % 3x2 matrix
>> B = randn(3,2); % random 3x2 matrix
>> scal_prod = trace(A'*B); % scalar product between A and B
>> scal_prod = A(:)'*B(:); % this is the same as the scalar product between the
% vectorized forms of A, B

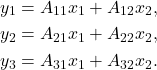
![Rendered by QuickLaTeX.com \[ y = x_{1} \begin{pmatrix} A_{11} \\ A_{21} \\ A_{31} \end{pmatrix} + x_{2} \begin{pmatrix} A_{12} \\ A_{22} \\ A_{32} \end{pmatrix}.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e0166c541c0595a738ccf91c8ffd5028_l3.png)
![Rendered by QuickLaTeX.com \[\begin{aligned} y_1 & =\begin{pmatrix} A_{11} \\ A_{12} \end{pmatrix}^{T} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = A_{11}x_{1} + A_{12}x_{2}, \\ y_2 & =\begin{pmatrix} A_{21} \\ A_{22} \end{pmatrix}^{T} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = A_{21}x_{1} + A_{22}x_{2}, \\ y_3 & =\begin{pmatrix} A_{31} \\ A_{32} \end{pmatrix}^{T} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = A_{31}x_{1} + A_{32}x_{2} \\ \end{aligned}\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4b7d6631e4b41c21aeedeba885efbaf6_l3.png)