Gram matrix

L. El Ghaoui

Gram matrix

Consider $m$ $n$ -vectors $x_1, \cdots, x_m$ . The Gram matrix of the collection is the $m\times m$ matrix $G$ with elements $G_{ij}=x_i^Tx_j$ . The matrix can be expressed compactly in terms of the matrix $X = [x_1, \cdots, x_m]$ , as

$G=X^T X=\left(\begin{array}{c} x_1^T \\ \vdots \\ x_m^T \end{array}\right)\left(\begin{array}{lll} x_1 & \ldots & x_m \end{array}\right).$

By construction, a Gram matrix is always symmetric, meaning that $G_{ij} = G_{ji}$ for every pair $(i,j)$ . It is also positive semi-definite, meaning that $u^TGu \ge 0$ for every vector $u \in \mathbb{R}^n$ (this comes from the identity $u^TGu = ||Xi||_2^2$ ).

Assume that each vector $x_i$ is normalized: $||x_i||_2 =1$ . Then the coefficient $G_{ij}$ can be expressed as

$G_{ij} = \cos \theta_{ij},$

where $\theta_{ij}$ is the angle between the vectors $x_i$ and $x_j$ . Thus $G_{ij}$ is a measure of how similar $x_i$ and $x_j$ are.

The matrix $G$ arises for example in text document classification, with $G_{ij}$ a measure of similarity between the 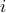-th and 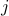-th document, and $x_i, x_j$ their respective bag-of-words representation (normalized to have Euclidean norm $1$ ).

See also:

Gram matrix

License

Share This Book