"

Definition: vector norm

Informally, a (vector) norm is a function which assigns a length to vectors.

Any sensible measure of length should satisfy the following basic properties: it should be a convex function of its argument (that is, the length of an average of two vectors should be always less than the average of their lengths); it should be positive-definite (always non-negative, and zero only when the argument is the zero vector), and preserve positive scaling (so that multiplying a vector by a positive number scales its norm accordingly).

Formally, a vector norm is a function f:\mathbb{R}^n \rightarrow \mathbb{R} which satisfies the following properties.

Definition of a vector norm
  1. Positive homogeneity: for every 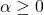x \in \mathbb{R}^n, \alpha \ge 0, we have f(\alpha x) = \alpha f(x).
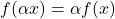  2. Triangle inequality: for every 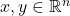x, y \in \mathbb{R}^n , we have
f(x+y) \leq f(x)+f(y)
  1. Definiteness: for every 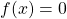x \in \mathbb{R}^n, f(x)=0 implies x=0.

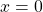A consequence of the first two conditions is that a norm only assumes non-negative values, and that it is convex.

Popular norms include the so-called l_p-norms, where p=1,2 or p=\infty:

||x||_p := \left(\sum\limits_{i=1}^{n} |x_i|^p\right)^{1/p},

with the convention that when p=\infty, ||x||_\infty = \max_{1\leq i \leq n} |x_i|.

License

Hyper-Textbook: Optimization Models and Applications Copyright © by L. El Ghaoui. All Rights Reserved.

Share This Book