Hyperplanes and half-spaces
Hyperplanes
A hyperplane is a set described by a single scalar product equality. Precisely, an hyperplane in ![]() is a set of the form
is a set of the form
where ![]() ,
, ![]() , and
, and ![]() are given. When
are given. When ![]() , the hyperplane is simply the set of points that are orthogonal to
, the hyperplane is simply the set of points that are orthogonal to ![]() ; when
; when ![]() , the hyperplane is a translation, along direction
, the hyperplane is a translation, along direction ![]() , of that set.
, of that set.
If ![]() , then for any other element
, then for any other element ![]() , we have
, we have
Hence, the hyperplane can be characterized as the set of vectors ![]() such that
such that ![]() is orthogonal to
is orthogonal to ![]() :
:
Hyperplanes are affine sets, of dimension ![]() (see the proof here). Thus, they generalize the usual notion of a plane in
(see the proof here). Thus, they generalize the usual notion of a plane in ![]() . Hyperplanes are very useful because they allow to separate the whole space into two regions. The notion of half-space formalizes this.
. Hyperplanes are very useful because they allow to separate the whole space into two regions. The notion of half-space formalizes this.
Example:
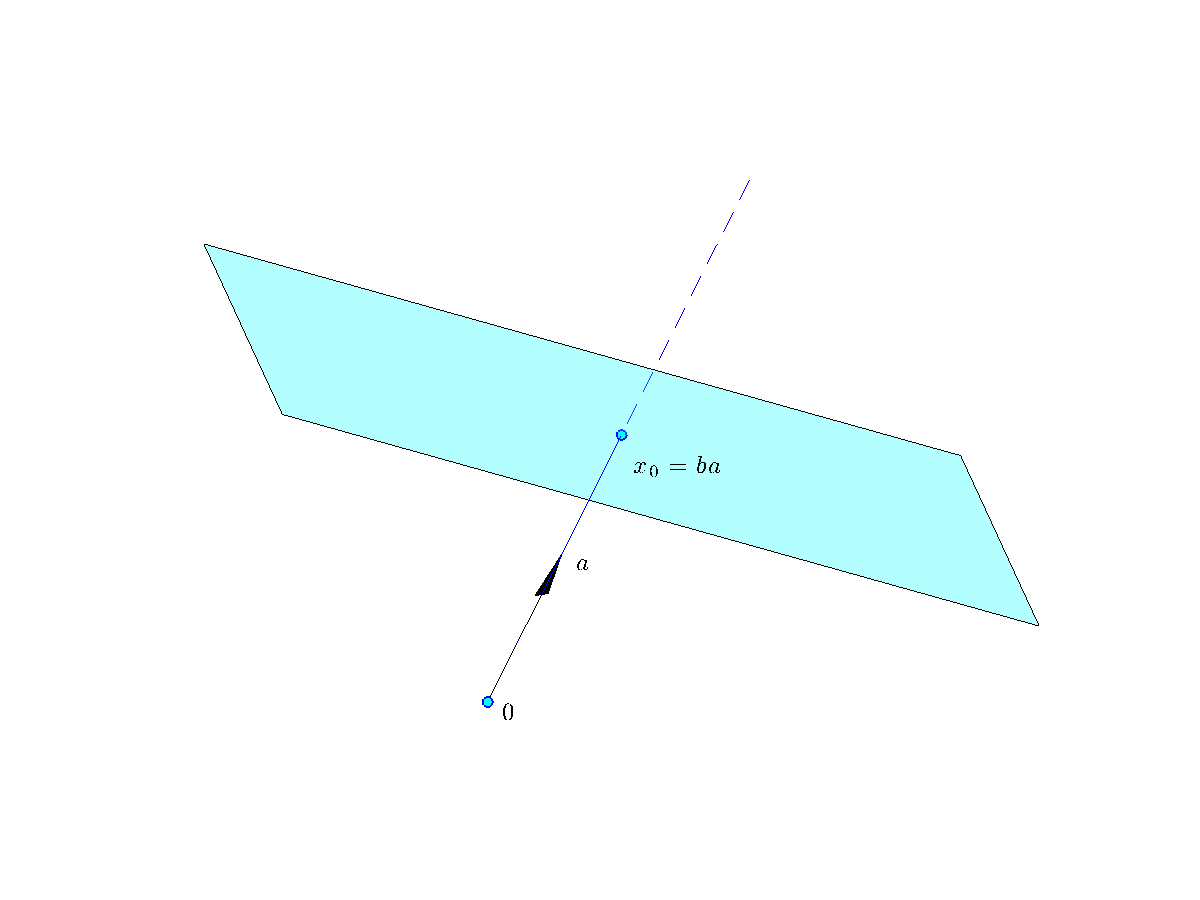
Projection on a hyperplane
Consider the hyperplane ![]() , and assume without loss of generality that
, and assume without loss of generality that ![]() is normalized (
is normalized (![]() ). We can represent
). We can represent ![]() as the set of points
as the set of points ![]() such that
such that ![]() is orthogonal to
is orthogonal to ![]() , where
, where ![]() is any vector in
is any vector in ![]() , that is, such that
, that is, such that ![]() . One such vector is
. One such vector is ![]() .
.
By construction, ![]() is the projection of
is the projection of ![]() on
on ![]() . That is, it is the point on
. That is, it is the point on ![]() closest to the origin, as it solves the projection problem
closest to the origin, as it solves the projection problem
Indeed, for any ![]() , using the Cauchy-Schwartz inequality:
, using the Cauchy-Schwartz inequality:
and the minimum length ![]() is attained with
is attained with ![]() .
.
Geometry of hyperplanes
Half-spaces
A half-space is a subset of ![]() defined by a single inequality involving a scalar product. Precisely, a half-space in
defined by a single inequality involving a scalar product. Precisely, a half-space in ![]() is a set of the form
is a set of the form
where ![]() ,
, ![]() , and
, and ![]() are given.
are given.
Geometrically, the half-space above is the set of points such that ![]() , that is, the angle between
, that is, the angle between ![]() and
and ![]() is acute (in
is acute (in ![]() ). Here
). Here ![]() is the point closest to the origin on the hyperplane defined by the equality
is the point closest to the origin on the hyperplane defined by the equality ![]() . (When
. (When ![]() is normalized, as in the picture,
is normalized, as in the picture, ![]() .)
.)
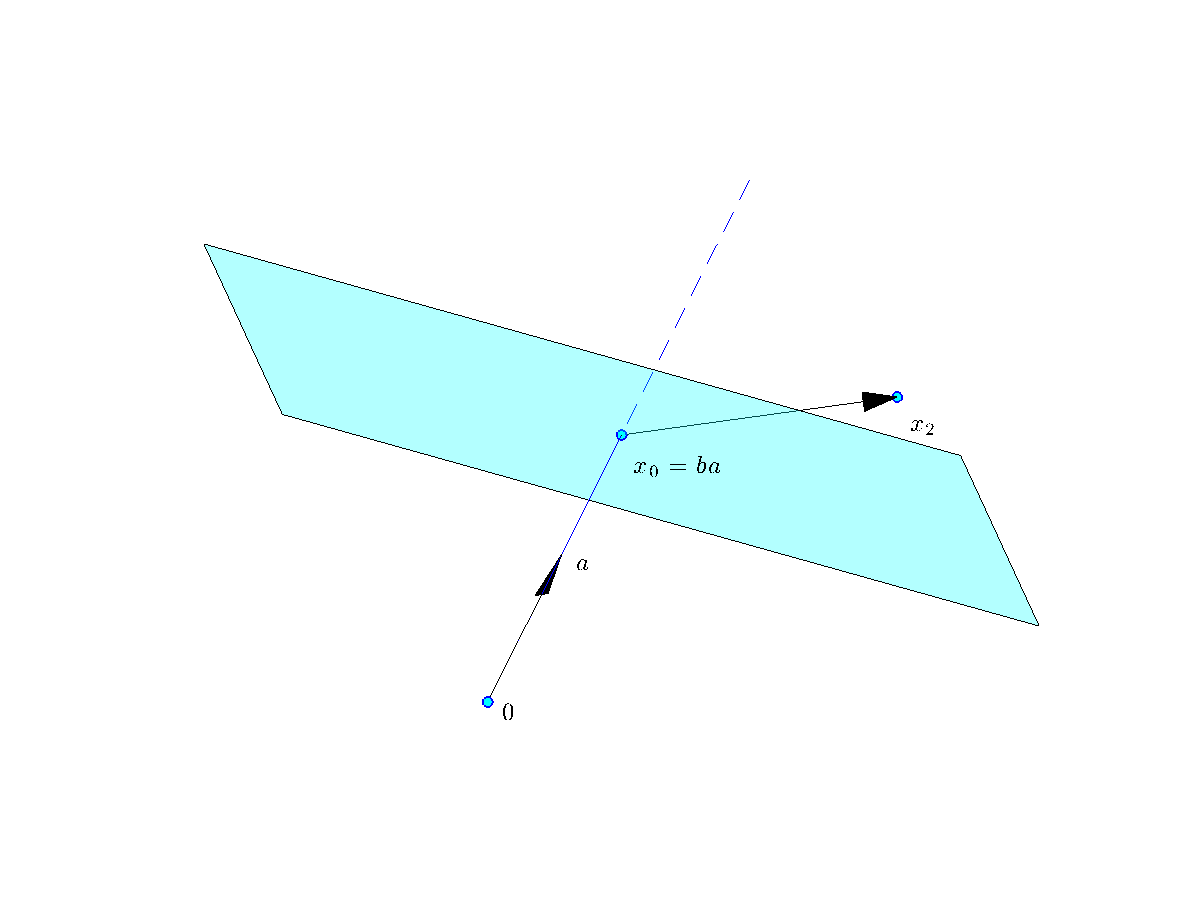 |
The half-space |