Rank-one matrices
Recall that the rank of a matrix is the dimension of its range. A rank-one matrix is a matrix with a rank equal to one. Such matrices are also called dyads.
We can express any rank-one matrix as an outer product.
The interpretation of the corresponding linear map ![]() for a rank-one matrix
for a rank-one matrix ![]() is that the output
is that the output ![]() is always in the direction
is always in the direction ![]() , with a coefficient of proportionality a linear function of
, with a coefficient of proportionality a linear function of ![]() :
: ![]() .
.
We can always scale the vectors ![]() and
and ![]() in order to express
in order to express ![]() as
as
![]()
where ![]() , with
, with ![]() , and
, and ![]() .
.
The interpretation for the expression above is that the result of the map ![]() for a rank-one matrix
for a rank-one matrix ![]() can be decomposed into three steps:
can be decomposed into three steps:
- we project
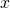 on the
on the  -axis, getting a number
-axis, getting a number 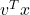 ;
; - we scale that number by the positive number
 ;
; - we lift the result (which is the scalar
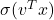 ) to get a vector proportional to
) to get a vector proportional to 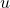 .
.
See also: Single factor model of financial price data.
