An hyperplane in 3D
Consider an affine set of dimension ![]() in
in ![]() , which we describe as the set of points
, which we describe as the set of points ![]() such that there exists two parameters
such that there exists two parameters ![]() such that
such that
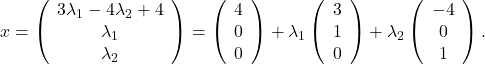
The set ![]() can be represented as a translation of a linear subspace:
can be represented as a translation of a linear subspace: ![]() , with
, with
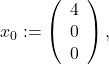
and ![]() the span of the two independent vectors
the span of the two independent vectors
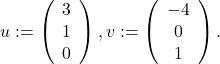
Thus, the set ![]() is of dimension
is of dimension ![]() in
in ![]() , hence it is an hyperplane. In
, hence it is an hyperplane. In ![]() , hyperplanes are ordinary planes.
, hyperplanes are ordinary planes.
We can find a representation of the hyperplane in the standard form
We simply find ![]() that is orthogonal to both
that is orthogonal to both ![]() and
and ![]() . That is, we solve the equations
. That is, we solve the equations
The above leads to ![]() . Choosing for example
. Choosing for example ![]() leads to
leads to ![]() .
.

