Matrix Inverses

L. El Ghaoui

Matrix Inverses

Square full-rank matrices and their inverse
Full column rank matrices and left inverses
Full-row rank matrices and right inverses

Square full-rank matrices and their inverse

A square $n \times n$ matrix is said to be invertible if and only if its columns are independent. This is equivalent to the fact that its rows are independent as well. An equivalent definition states that a matrix is invertible if and only if its determinant is non-zero.

For invertible $n \times n$ matrices $A$ , there exist a unique matrix $B$ such that $AB = BA = I_{n}$ . The matrix $B$ is denoted $A^{-1}$ and is called the inverse of $A$ .

Example: a simple 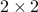2 times 2 matrix.

If a matrix $R$ is square, invertible, and triangular, we can compute its inverse $R^{-1}$ simply, as follows. We solve $n$ linear equations of the form $Rx_{i}=e_{i}, i =1, \dots, n,$ with $e_{i}$ the $i$ -th column of the $n \times n$ identity matrix, using a process known as backward substitution. Here is an example. At the outset, we form the matrix $R^{-1} = [x_{1}, \dots, x_{n}].$ By construction, $R \cdot R^{-1} = I_{n}$ .

For general square, invertible matrices $A$ , the QR decomposition allows computing the inverse. For such matrices, the QR decomposition is of the form $A = QR$ , with $Q$ a $n \times n$ orthogonal matrix, and $R$ is upper triangular. Then the inverse is $A^{-1}=R^{-1}Q^{T}$ .

Matlab syntax

Ainv = inv(A); % produces the inverse of a square, invertible matrix

A useful property is the expression of the inverse of a product of two square, invertible matrices $A, B$ : $(AB)^{-1}=B^{-1}A^{-1}.$ (Indeed, you can check that this inverse works.)

Full column rank matrices and left inverses

A $m \times n$ matrix is said to be full column rank if its columns are independent. This necessarily implies $m \ge n$ .

A matrix $A$ has full column rank if and only if there exists a $n \times m$ matrix $B$ such that $BA=I_{n}$ (here $n \le m$ is the small dimension). We say that $B$ is a left-inverse of $A$ . To find one left inverse of a matrix with independent columns $A$ , we use the full QR decomposition of $A$ to write

$A = Q \begin{pmatrix} R_{1} & 0 \end{pmatrix},$

where $R_{1}$ is $n \times n$ upper triangular and invertible, while $Q$ is $m \times m$ and orthogonal ( $Q^{T}Q = I_{m}$ ). We can then set a left inverse $B$ to be

$B = \begin{pmatrix} R_{1}^{-1} \\ 0 \end{pmatrix}Q^{T}.$

The particular choice above can be expressed in terms of $A$ directly:

$B = (A^{T}A)^{-1}A^{T}.$

Note that $A^{T}A$ is invertible, as it is equal to $R_{1}^{T}R_{1}$ .

In general, left inverses are not unique.

Full-row rank matrices and right inverses

A $m \times n$ matrix is said to be full row rank if its rows are independent. This necessarily implies $m \le n.$ .

A matrix $A$ has full row rank if and only if there exists a $n \times m$ matrix $B$ such that $AB=I_{m}$ (here $m \le n$ is the small dimension). We say that $B$ is a right-inverse of $A$ . We can derive expressions of right inverses by noting that $A$ is full row rank if and only if $A^{T}$ is full column rank. In particular, for a matrix with independent rows, the full QR decomposition (of $A^{T}$ ) allows writing

$A = \begin{pmatrix} R_{1}^{T} & 0 \end{pmatrix} Q^{T},$

where $R_{1}$ is $m \times m$ upper triangular and invertible, while $Q$ is $n \times n$ and orthogonal ( $Q^{T}Q = I_{n}$ ). We can then set a right inverse of $A$ to be

$B = Q \begin{pmatrix} R_{1}^{-1} \\ 0 \end{pmatrix}.$

The particular choice above can be expressed in terms of $A$ directly:

$B = A^{T}(AA^{T})^{-1}.$

Note that $AA^{T}$ is invertible, as it is equal to $R_{1}^{T}R_{1}$ .

In general, right inverses are not unique.

Matrix Inverses

Square full-rank matrices and their inverse

Full column rank matrices and left inverses

Full-row rank matrices and right inverses

License

Share This Book