Dual Norm

L. El Ghaoui

Dual Norm

For a given norm $||\cdot||$ on $\mathbb{R}^n$ , the dual norm, denoted $||\cdot||_*$ , is the function from $\mathbb{R}^n$ to $\mathbb{R}$ with values

$||y||_*=\max\limits_{x}x^Ty: ||x|| \leq 1.$

The above definition indeed corresponds to a norm: it is convex, as it is the pointwise maximum of convex (in fact, linear) functions $x \rightarrow y^Tx$ ; it is homogeneous of degree $1$ , that is, $||\alpha x||_* = \alpha ||x||_*$ for every $x \in \mathbb{R}^n$ and $\alpha \ge 0$ .

By definition of the dual norm,

$x^Ty \leq ||x||\cdot ||y||_*.$

This can be seen as a generalized version of the Cauchy-Schwartz inequality, which corresponds to the Euclidean norm.

Examples:

The norm dual to the Euclidean norm is itself. This comes directly from the Cauchy-Schwartz inequality.
The norm dual to the 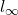$l_\infty$ -norm is the 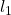$l_1$ -norm. This is because the inequality

$x^Ty \leq ||x||_\infty \cdot ||y||_1.$

holds trivially, and is attained for $x = {\bf sign}(y)$ .

The dual norm above is the original norm we started with. (The proof of this general result is more involved.)

Dual Norm

License

Share This Book