Minimization of a convex quadratic function
Here we consider the problem of minimizing a convex quadratic function without any constraints. Specifically, consider the problem

where  , and
, and 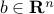 . We assume that
. We assume that 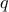 is convex, meaning that its Hessian
is convex, meaning that its Hessian  is positive semi-definite.
is positive semi-definite.
The optimality condition for an unconstrained problem is  , which here reduces to
, which here reduces to

Case when  is positive-definite
is positive-definite
When  is positive-definite, that is, it has only positive (non-zero) eigenvalues, then there is a unique minimizer. The above optimality condition provides it:
is positive-definite, that is, it has only positive (non-zero) eigenvalues, then there is a unique minimizer. The above optimality condition provides it:  .
.
Degenerate case: a simple example
Consider the case with

The optimality condition is

These equations are feasible if and only  (that is,
(that is, 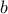 is in the range of
is in the range of  ). In that case, the set of optimal points are of the form
). In that case, the set of optimal points are of the form  ,
, 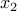 arbitrary.
arbitrary.
Otherwise, when  , the optimality conditions are not feasible, and the minimum value is actually
, the optimality conditions are not feasible, and the minimum value is actually  . It is only attained in the limit, for example with
. It is only attained in the limit, for example with 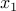 fixed arbitrarily,
fixed arbitrarily,  , with sign of
, with sign of 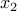 equal to that of
equal to that of  .
.
General case
If  is not invertible, but
is not invertible, but 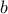 is in the range of
is in the range of  , then there exist
, then there exist 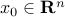 such that
such that  . Then any point
. Then any point  such that
such that 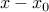 is in the nullspace of
is in the nullspace of  is optimal, since
is optimal, since

In particular, 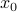 is optimal, and the corresponding value of the problem is
is optimal, and the corresponding value of the problem is  .
.
If 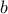 is not in the range space of
is not in the range space of  , then there are no minimizing points. This means that the minimum is not attained. We can in fact show that
, then there are no minimizing points. This means that the minimum is not attained. We can in fact show that  , and construct a sequence of points that achieves this value in the limit. We simply invoke the fundamental theorem of linear algebra. For symmetric matrices, the theorem specializes to the fact that range and nullspace are orthogonal. Since
, and construct a sequence of points that achieves this value in the limit. We simply invoke the fundamental theorem of linear algebra. For symmetric matrices, the theorem specializes to the fact that range and nullspace are orthogonal. Since  ,
, 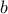 can be written as
can be written as  , with
, with  and
and  . Set
. Set  , with
, with 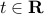 ; since
; since  , we obtain
, we obtain  . Letting
. Letting  achieves the desired result.
achieves the desired result.
Proof via the eigenvalue decomposition
A constructive proof involves the eigenvalue decomposition of the symmetric matrix  . We have
. We have 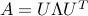 , with
, with 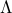 a diagonal matrix containing the (non-negative) eigenvalues of
a diagonal matrix containing the (non-negative) eigenvalues of  , and
, and 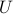 an orthogonal matrix of eigenvectors. The original problem can be expressed in terms of the new variable
an orthogonal matrix of eigenvectors. The original problem can be expressed in terms of the new variable  , as follows:
, as follows:

with  . Now decompose
. Now decompose 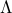 as
as  with
with  containing the positive eigenvalues. We decompose the variable
containing the positive eigenvalues. We decompose the variable 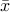 as
as  , with vector
, with vector  (resp.
(resp.  ) the variables corresponding to the positive (resp. zero) eigenvalues. Decompose
) the variables corresponding to the positive (resp. zero) eigenvalues. Decompose  similarly, as
similarly, as  . The problem writes
. The problem writes

The problem looks exactly like the simple 2D example above.
The optimality conditions then write

If  , the solutions are of the form
, the solutions are of the form  , with
, with  free. (We recover a unique solution when there are no zero eigenvalues, that is,
free. (We recover a unique solution when there are no zero eigenvalues, that is,  is invertible.)
is invertible.)
Otherwise, there are no optimal points. Choosing  , with
, with  , achieves the optimal value
, achieves the optimal value  .
.
