Incidence matrix of a network
Mathematically speaking, a network is a graph of 
nodes connected by 
directed arcs. Here, we assume that arcs are ordered pairs, with at most one arc joining any two nodes; we also assume that there are no self-loops (arcs from a node to itself). We do not assume that the edges of the graph are weighted — they are all similar.
We can fully describe the network with the so-called arc-node incidence matrix, which is the 
matrix defined as
![\[A_{ij} = \begin{cases} 1 \text{ if arc $j$ starts at node $i$} \\ -1 \text{ if arc $j$ ends at node $i, 1 \le i \le m, 1 \le j \le n$}. \\ 0 \text{ otherwise.} \end{cases}.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d817cb38ad0754dc3c42f4c85a6fadfb_l3.png "Rendered by QuickLaTeX.com")
 |
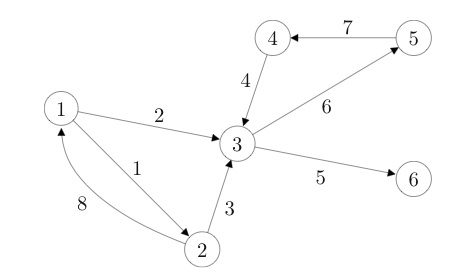The figure shows the graph associated with the arc-node incidence matrix
|
![\[A=\begin{bmatrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 & -1 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & -1 & -1 & -1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \end{bmatrix}.\]](https://ecampusontario.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0240749f8991d33b34115640c55af4e1_l3.png "Rendered by QuickLaTeX.com")
See also: Network flow.