Full Rank Matrices

L. El Ghaoui

Full Rank Matrices

Theorem

A matrix $A \in \mathbb{R}^{m \times n}$ is

full column rank if and only if 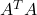$A^{T}A$ is invertible.
full row rank if and only if 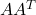$AA^{T}$ is invertible.

Proof: The matrix is full column rank if and only if its nullspace if reduced to the singleton $\{0\}$ , that is,

$A x=0 \Longrightarrow x=0 .$

If $A^T A$ is invertible, then indeed the condition $A x=0$ implies $A^T A x=0$ , which in turn implies $x=0$ .
Conversely, assume that the matrix is full column rank, and let $x$ be such that $A^T A x=0$ . We then have $x^T A^T A x=\|A x\|_2^2=0$ , which means $A x=0$ . Since $A$ is full column rank, we obtain $x=0$ , as desired.
The proof for the other property follows similar lines.

Full Rank Matrices

License

Share This Book