Absorption spectrometry: using measurements at different light frequencies

L. El Ghaoui

Absorption spectrometry: using measurements at different light frequencies

The Beer-Lambert law postulates that the logarithm of the ratio of the light intensities is a linear function of the concentrations of each gas in the mix. The log-ratio of intensities is thus of the form $y = a^{T}x$ for some vector $a \in \mathbb{R}^{n}$ , where $x$ is the vector of concentrations, and the vector $a \in \mathbb{R}^{n}$ contains the coefficients of absorption of each gas. This vector is actually also a function of the frequency of the light we illuminate the container with.

Now consider a container having a mixture of $n$ ‘‘pure’’ gases in it. Denote by $x \in \mathbb{R}^{n}$ the vector of concentrations of the gases in the mixture. We illuminate the container at different frequencies $\lambda_{1},\dots, \lambda_{m}$ . For each experiment, we record the corresponding log-ratio $y_{i}, i = 1, \dots, m$ , of the intensities. If the Beer-Lambert law is to be believed, then we must have

$y_{i} = a_{i}^{T}x, i = 1,\dots,m,$

for some vectors $a_{i} \in \mathbb{R}^{n}$ , which contain the coefficients of absorption of the gases at light frequency $\lambda_{i}$ . More compactly:

$y=Ax$

where

$A = \begin{pmatrix} a_{1}^{T} \\ \vdots \\ a_{m}^{T} \end{pmatrix}.$

Thus, $A_{ij}$ is the coefficient of absorption of the 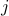-th gas at frequency $\lambda_{i}$ .

Since $A_{ij}$ ‘s correspond to ‘‘pure’’ gases, they can be measured in the laboratory. We can then use the above model to infer the concentration of the gases in a mixture, given some observed light intensity log-ratio.

Absorption spectrometry: using measurements at different light frequencies

License

Share This Book