Variants of the Least-Squares Problem

L. El Ghaoui

Variants of the Least-Squares Problem

Linearly-constrained least-squares
Minimum-norm solutions to linear equations
Regularized least-squares

Linearly constrained least-squares

Definition

An interesting variant of the ordinary least-squares problem involves equality constraints on the decision variable $x$ :

$\min _x\|A x-y\|_2^2 ; \quad C x=d_1$
where $C \in \mathbf{R}^{p \times n}$ , and $d \in \mathbf{R}^p$ are given.

Examples:

Minimum-variance portfolio.

Solution

We can express the solution by first computing the null space of $C$ . Assuming that the feasible set of the constrained iS problem is not empty, that is, $d$ is in the range of $C$ , this set can be expressed as
$\mathbf{X}=\left\{x_0+N z: z \in \mathbf{R}^k\right\},$
where $k$ is the dimension of the nullspace of $C, N$ is a matrix whose columns span the nullspace of $C$ , and $x_0$ is a particular solution to the equation $C x=d$ .
Expressing $x$ in terms of the free variable $z$ , we can write the constrained problem as an unconstrained one:
$\begin{aligned} \min _{\bar{s}}\|\bar{A} z-\bar{y}\|_2 \text {, } \\ \text { where } \bar{A}:=A N \text {, and } \tilde{y}=y-A x_0 . \end{aligned}$

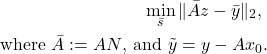
Minimum-norm solution to linear equations

A special case of linearly constrained LS is
$\min _x\|x\|_2: A x=y,$
in which we implicitly assume that the linear equation in $x: A x=y$ , has a solution, that is, $y$ is in the range of $A$ .
The above problem allows selecting a particular solution to a linear equation, in the case when there are possibly many, that is, the linear system $A x=y$ is under-determined.
As seen here, when $A$ is full row rank, that is, the matrix $A A^T$ is invertible, the above has the closed-form solution
$x^*=A^T\left(A A^T\right)^{-1} y .$

Examples: Control positioning of a mass.

Regularized least-squares

In the case when the matrix $A$ in the OLS problem is not full column rank, the closed-form solution cannot be applied. A remedy often used in practice is to transform the original problem into one where the full column rank property holds.

The regularized least-squares problem has the form

$\min _x\|A x-y\|_2^2+\lambda \mid x \|_2^2,$
where $\lambda>0$ is a (usually small) parameter.
The regularized problem can be expressed as an ordinary least-squares problem, where the data matrix is full column rank, Indeed, the above problem can be written as the ordinary LS problem $\min _x\|\bar{A} x-\bar{y}\|_2^2$ ,
where
$\tilde{A}:=\left(\begin{array}{c} A \\ \sqrt{\lambda} I_n \end{array}\right), \bar{y}:=\left(\begin{array}{c} y \\ 0 \end{array}\right) .$
The presence of the identity matrix in the $(m+n) \times n$ matrix $\bar{A}$ ensures that it is full (column) rank.

Solution

Since the data matrix in the regularized LS problem has full column rank, the formula seen here applies. The solution is unique and given by

$x^*=(\tilde{A}^T\tilde{A})^{-1}\tilde{A}^T\tilde{y}=(A^TA+\lambda I_n)^{-1}A^Ty$

For $\lambda=0$ , we recover the ordinary LS expression that is valid when the original data matrix is full rank.

The above formula explains one of the motivations for using regularized least-squares in the case of a rank-deficient matrix $A$ : if $\lambda>0$ , but is small, the above expression is still defined, even if $A$ is rank-deficient.