18 Solving triangular systems of equations: backwards substitution example
Consider the triangular system
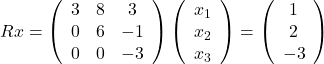
we solve for the last variable ![]() first, obtaining (from the last equation)
first, obtaining (from the last equation) ![]() . We plug this value of
. We plug this value of ![]() into the first and second equation, obtaining a new triangular system in two variables
into the first and second equation, obtaining a new triangular system in two variables ![]() :
:
We proceed by solving for the last variable ![]() . The last equation yields
. The last equation yields ![]() . Plugging this value into the first equation gives
. Plugging this value into the first equation gives ![]() .
.
We can apply the idea to find the inverse of the square upper triangular matrix ![]() , by solving
, by solving
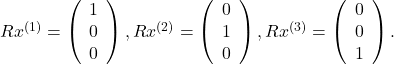
The matrix ![]() is then the inverse of
is then the inverse of ![]() . We find
. We find
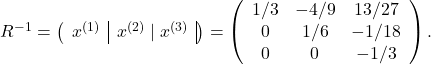
As illustrated above, the inverse of a triangular matrix is triangular.
