Singular Value Decomposition of General Matrices

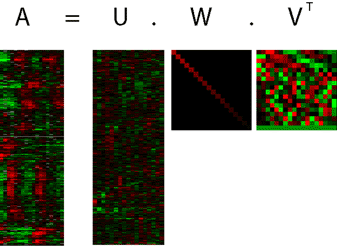
The singular value decomposition (SVD) generalizes the spectral theorem (available for a square, symmetric matrix), to any non-symmetric, and even rectangular, matrix. The SVD allows to describe the effect of a matrix on a vector (via the matrix-vector product), as a three-step process: a first rotation in the input space; a simple positive scaling that takes a vector in the input space to the output space; and another rotation in the output space. The figure on the left shows the SVD of a matrix of biological data.

The SVD allows to analyze matrices and associated linear maps in detail, and solve a host of special optimization problems, from solving linear equations to linear least-squares. It can also be used to reduce the dimensionality of high-dimensional data sets, by approximating data matrices with low-rank ones. This technique is closely linked to the principal component analysis method.

Outline

• The SVD theorem
• Matrix properties via SVD
• Solving linear systems via SVD
• Least-squares and SVD
• Low-rank approximations
• Applications
• Exercises