Singular value decomposition of a 4×5 matrix

L. El Ghaoui

Singular value decomposition of a 4×5 matrix

Consider the matrix

$A=\left(\begin{array}{lllll} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 & 0 \end{array}\right)$

A singular value decomposition of this matrix is given by $A=U \tilde{S} V^T$ , with

$U=\left(\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & -1 \\ 1 & 0 & 0 & 0 \end{array}\right), \tilde{S}=\left(\begin{array}{ccccc} 4 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 \\ 0 & 0 & \sqrt{5} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right), \quad V^T=\left(\begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ \sqrt{0.2} & 0 & 0 & 0 & \sqrt{0.8} \\ 0 & 0 & 0 & 1 & 0 \\ -\sqrt{0.8} & 0 & 0 & 0 & \sqrt{0.2} \end{array}\right) .$

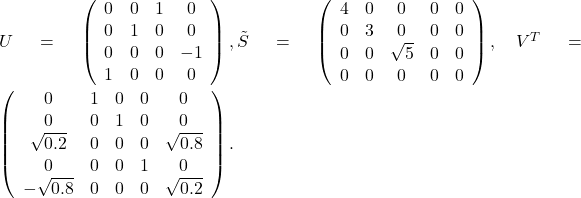
Notice above that 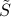tilde{ {S}} has non-zero values only in its diagonal and can be written as

$\tilde{S}=diag(S,0,0), S:=diag(\sigma_1,\sigma_2,\sigma_3),$

with $\sigma_1=4$ , $\sigma_2=3$ , $\sigma_3=\sqrt{5}$ . The rank of $A$ (which is the number of non-zero elements on the diagonal matrix $\tilde{S}$ ) is thus $r=3<min(m,n)$ . We can check that $V^TV=VV^T=I_5$ , and $UU^T=U^TU=I_4$ .

See also:

Singular value decomposition of a 4×5 matrix

License

Share This Book