Sensitivity Analysis

L. El Ghaoui

Sensitivity Analysis

Least-Squares > Ordinary LS | Variants | Sensitivity | Applications

Relative error analysis
Condition number

We consider the OLS problem:

$\min _x\|A x-y\|_2$

with

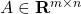$A \in \mathbf{R}^{m \times n}$ the data matrix (known);
$y \in \mathbf{R}^m$ is the measurement (known);
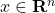$x \in \mathbf{R}^n$ is the vector to be estimated (unknown).

We assume that $A$ is full column rank. Then, the solution $\hat{x}_{\mathrm{L} S}$ to the OLS problem is unique, and can be written as a linear function of the measurement vector $y$ :

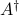$\hat{x}_{\mathrm{LS}}=A^{\dagger} y,$

with A^dagger the pseudo-inverse of $A$ . Again, since $A$ is full column rank,

$A^{\dagger}=\left(A^T A\right)^{-1} A^T .$

We are interested in analyzing the impact of perturbations in the vector $y$ , on the resulting solution $\hat{x}_{\mathrm{LS}}$ . We begin by analyzing the absolute errors in the estimate and then turn to the analysis of relative errors.

Bound on the absolute error

We first try to find a bound on the error in the solution given a bound on the error in the input. Let us assume a simple model of potential perturbations: we assume that $\delta y$ belongs to a unit ball: $\|\delta y\|_2 \leq \alpha$ , where $\alpha > 0$ is given. We will assume $\alpha =1$ for simplicity; the analysis is easily extended to any $\alpha > 0$ .

Let us define $\hat{x}_{1 S}+\delta x$ to be the estimate corresponding to the measurement $y+\delta y$ , that is:

$\hat{x}_{\mathrm{LS}}+\delta x=A^{\dagger}(y+\delta y) .$

Since $\hat{x}_{\mathrm{LS}}=A^{\dagger} y$ , we have

$\delta x=A^{\dagger} \delta y .$

We obtain that

$\|\delta x\|_2 \leq\left\|A^{\dagger}\right\| \cdot\|\delta y\|_2,$

where $\|\cdot\|$ is the matrix norm, which is defined for a matrix $B$ as

$\|B\|:=\max _{x:\|x\|_2 \leq 1}\|B x\|_2 .$

In other words, $\|B\|$ is simply the maximum output norm that we can attain with a unit-norm input. (The matrix norm can be computed from an SVD of the matrix $B$ .)

The interpretation is that $\left\|A^{\dagger}\right\|$ is the largest absolute error that can result from an absolute error in the input $y$ that is bounded by $1$ .

Bound on the relative error analysis

We now turn to the problem of analyzing the impact of relative errors in the measurement, on the relative error in the solution.

To simplify, let us assume that the matrix $A$ is square ( $m=n$ ) and full rank (invertible). The development before simplifies to

$\delta x=\left(A^T A\right)^{-1} A^T y=A^{-1} \delta y,$

so that

$\|\delta x\|_2 \leq\left\|A^{-1}\right\| \cdot\|\delta y\|_2 .$

Likewise, the equation $A x=y$ allows to bound $\|x\|_2$ with respect to $\|y\|_2$ :

$\|y\|_2 \leq\|A\| \cdot\|x\|_2 .$

Combining the two inequalities we obtain:

$\frac{\|\delta x\|_2}{\|x\|_2} \leq\left(\|A\| \cdot\left\|A^{-1}\right\|\right) \cdot \frac{\|\delta y\|_2}{\|y\|_2} .$

Condition number

As seen above, when $A$ is square and invertible, the quantity

$\kappa(A):=\|A\| \cdot\left\|A^{-1}\right\|$

measures the sensitivity to relative errors in the system $Ax=y$ .

The quantity above is called the condition number of $A$ . The condition number is always greater than $1$ . The closer to $1$ , the more confident we can be about the solution $x$ when $y$ is subject to small relative errors. We can generalize this notion to non-necessarily square matrices that have full rank.

Many practical algorithms to solve linear equations (or OLS) use the condition number (or an estimate) to evaluate the quality of the solution.

Sensitivity Analysis

Bound on the absolute error

Bound on the relative error analysis

Condition number

License

Share This Book